Propositional and First Order Logic - Part 2

Introduction

Propositional Logic transforms a complete sentence into a symbol. It makes it logical, whereas, in First-Order Logic, a particular sentence will be made that involves relations, functions, and constants. This article has popular propositional and first-order logic questions in past year gate exams.

Questions

31. Which one of the following well-formed formulae is a tautology? [GATE-CS-2015 (Set 2)]

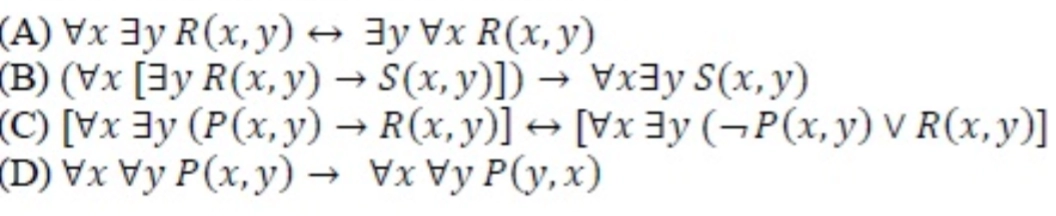
Answer: C

Explanation: In logic, a tautology is a true formula in every possible interpretation. All options here are based on the order of application of the quantifier. So, there are two rules:

• we can switch the positions of the same type of quantifiers
• we cannot switch the positions of different kinds of quantifiers.

Now, let's see the options of the question: Option (a) Sign <-> denotes "not equivalent".

∀x∃y R( x, y ) is not equal to ∃Y ∀X R( X, Y )

Let R( X, Y ) symbolize X < Y for the set of numbers as the universe, for example. Then ∀X ∃YR( X, Y ) reads "for every number x; there is a number y which is greater than x", which is true, while ∃Y ∀X R( X, Y ) reads "there is a number that is greater than every number", which is not true. So this option is rejected. Option (d) Sign -> represents "equivalent"

 ∀X ∀YR( X, Y ) is equivalent to ∀X ∀YR( Y, X )

Let R( X, Y ) denote X < Y for the set of numbers as the universe, for example. Then ∀X ∀YR( X, Y ) reads, "for every number X, there is every Y greater than x". In contrast, ∀X ∀YR( Y, X ) reads, "for every number Y, there is every X greater than Y,". And both can't be equivalent, so this option is rejected. Option (b) is rejected as two predicates can't be equal to one predicate only. So option (c) is the correct one. The explanation for option (c) – as the position of the quantifier is not varied and since LHS P -> R = ⌐P ᴠ R, which is equivalent to RHS. Option (c) is a tautology and correct answer too.

32. Let # be a binary operator represented as X # Y = X′ + Y′ where X and Y are Boolean variables. Consider the below statements. [GATE-CS-2015 (Set 3)]

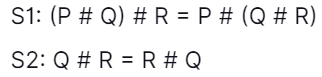
Which of the subsequent is/are true for the Boolean variables P, Q, and R?

Answer: B

Explanation: S2 is true, as Y' + X' = X' + Y'

S1 is false.

Let P = 1, Q = 1, R = 0, we get

33. Assume U is the power set of the set S = {1,2,3,4,5,6}. For any T ∈ U, let |T| indicate the number of elements in T and T′ denotes the complement of T. For any T, R ∈ U, let TR be the set of all the elements in T which are not in R. Which of the following is true? [GATE-CS-2015 (Set 3)]

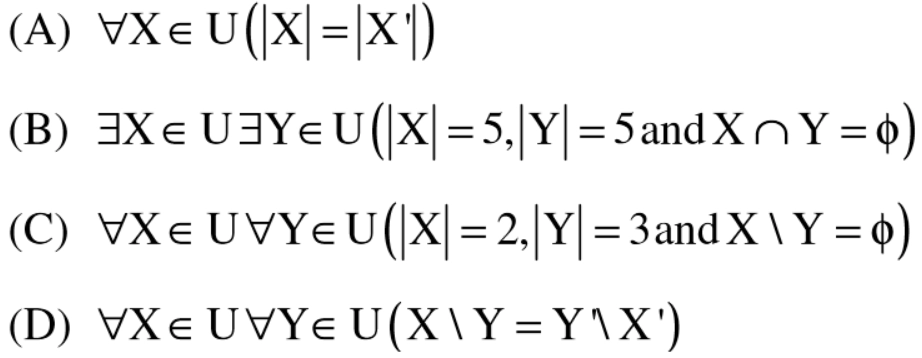
Answer: D

Explanation: A is false, Taking an example like X = {1, 2, 3, 4},

X' = {5, 6}, |X| is not same as |X'|.

B is false, as any two subsets of size 5 of U 

would have some common elements.

C is false,  Taking an example like X = {1, 2}

Y = {3, 4, 5}, X\Y = {1, 2}.

34. There are just two types of people in a room, i.e., Type 1 and Type 2. The Type 1 people always tell the truth, and Type 2 people always lie. You provide a fair coin to a person in that room without knowing the type he is from and tell him to toss and hide the result until you ask for it. Upon questioning, the person replies the following:

Which of the following options is correct? [GATE-CS-2015 (Set 3)]

Answer: A

Explanation:  

If the person is of Type 1 and always tells the truth, the result must behead.

If the person is Type 2 and always tells a lie, the result must behead.

Negation of the sentence of the form "X is true if and only if Y is true" is 

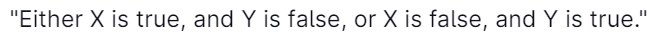
It means, "Either toss is head, and I am not telling the truth, or toss is tail

and I am telling the truth".

Since the person always lies, "Either toss his head, and I am not telling the truth."

35. Let p, q, r, & s be four primitive statements. Consider the following arguments: [GATE-IT-2004]

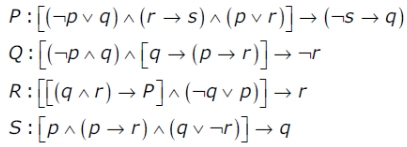
Which of the above arguments are valid?

A. P and Q only

B. P and R only

C. P and S only

D. P, Q, R and S

Answer: C

Explanation: Use Boolean logic minimization and get 1(TRUE) for validation.

eg: P:[(¬P∨Q)∧(r→S)∧(P∨R)]⇒(¬S→Q)P:[(¬P∨Q)∧(r→S)∧(P∨R)]⇒(¬S→Q)

≡(P¯+Q)(R¯+S)(P+R) +(S¯¯+Q)≡(P¯+Q)(R¯+S)(P+R)¯+(S¯¯+Q)

≡(PQ¯)+(RS¯)+(P¯Q¯)+(S+Q)≡(PQ¯)+(RS¯)+(P¯Q¯)+(S+Q)

≡Q¯(P+P¯)+(RS¯)+(S+Q)≡Q¯(P+P¯)+(RS¯)+(S+Q)

≡Q¯+RS¯+S+Q≡Q¯+RS¯+S+Q

≡TRUE(1)

36. Let P(x) and Q(x) be some arbitrary predicates. Which one of the below statements is always TRUE? [Gate IT 2005]

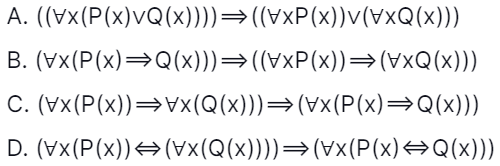
Answer: B

Explanation: Generally, we can solve these types of questions by using two statements and checking the validity of every option. Here, let the statements be P and Q where P: Student is a girl Q: Student is smart Option B says that IF for all student x: If x is a girl then the student is smart THEN IF the whole class comprises of girls then the entire class comprises of smart students.

37. Consider the below expressions: 

(i) true (ii) false  (iii) Q (iv) P ∨ Q (v) ¬Q ∨ P 

The number of expressions given above that are logically implied by P ∧ (P ⇒ Q) is ______________ [The Question was originally a Fill-in-the-blanks type] [GATE-CS-2016 (Set 2)]

A. 2

B. 3

C. 4

D. 5

Answer: C

Explanation: The answer is 4. 
The solution, say, X is 'Logically Implied' by [ P ∧ (P ⇒ Q) ], then [ P ∧ (P ⇒ Q) ] ⇒ X is always true, i.e., a tautology, so we can say that X is logically implied by P ∧ (P ⇒ Q), such that we need to find X for which [ P ∧ (P ⇒ Q) ] ⇒ X will always be true for all values of P, Q, and X. 
Look at the following table

Notice that the value of X doesn't matter if the premise of expression, i.e., Premise of [P ∧ (P ⇒ Q)] ⇒ X, such that [P ∧ (P ⇒ Q)] is 0, indicating the final expression would be a tautology for all values of X if [P ∧ (P ⇒ Q)] is 0. Still, if the premise is 1 (as in the last row), then X must be one so that the final implication, that is, [ P ∧ (P ⇒ Q) ] ⇒ X, is true for all values. If you replace X with all five options, we will find that for X = Q, True, P ∨ Q, ¬Q ∨ P, the stated expression would always be true for X = False, the expression would not be a tautology. Therefore # of expression is 4.

38. Which one of the below well-formed formulae in predicate calculus is NOT valid? [GATE-CS-2016 (Set 2)]

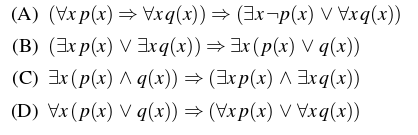
Answer: D

Explanation: Imagine if there are two statements, P and Q,

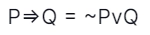
That is, the only situation where the implication is false (=>) is when P is true and Q is false. 

That is, A truth statement can't imply a false statement.

So, it will be better for these questions to take options and check for some arbitrary conditions.

By looking at the options, we are pretty sure that A, B are correct

Suppose X is any number and the statement is P(x) = X is a prime number

Q(x) = X is a non-prime number

If we look at option D,

Before implication: For all x, x is either prime or non-prime, which is true.

After implication: For all x, x is excellent, or for all x, x is non-prime, which is false, i.e., here, a truth statement implies a false statement that is not valid.

If we look at option C, there exists a number x, which is both prime & non-prime, that is false, and a false statement can indicate either true or false. So option (C) is correct. So, the answer is Option (D).

39. Which one of these first-order logic formulas is valid? [Gate IT 2007]

Answer: A

Explanation: (A) LHS->RHS

LHS: For all x (if P holds, then Q holds)

RHS: If P(x) holds for all x, then Q(x) has for all x.

(B) LHS !->RHS

LHS: An x exists for which either P(x) is true or Q(x) is true.

RHS: If an x exists for which P(x) is true, then another x exists for which Q(x) is true.

(C) both x doesn't need to be the same on RHS.

LHS: There exists an x for which both P(x) and Q(x) are true.

RHS: There is an x for which P(x) is true, and there is an x for which Q(x) is true.

(D) LHS!->RHS

LHS: For every x, there exists a y such that P(x, y) holds.

RHS: There exists a y such that for all x P(x, y) holds.

40. Which of the subsequent first-order formula is logically valid? Here α(x) is a first-order formula with x as a free variable, and β is a first-order formula with no free variable. [Gate IT 2008]

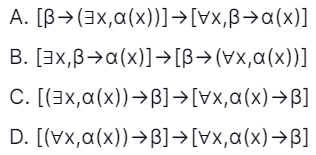
Answer: C

Explanation: A formula is logically correct if it is true in every interpretation. These formulas play a role identical to tautologies in propositional logic. A valid formula is one having no instance of it being false. It is sufficient to give an example confirming that our formula is not a good choice for this question.

Option (a) LHS: If β is true, then there exists an x for which α(x) is true. RHS: For all the x, if β is true, then α(x) is true. This is the same as saying if β is true, then for all the x, α(x) is true. (β⟹∀x,α(x)) Such that RHS⟹LHS and LHS⟹̸ RHS.

Option (b) LHS: There exists an x such that if the β is true, then α(x) is true. RHS: If the β is true, then for all x, α(x) is true. So, RHS⟹LHS and LHS⟹̸ RHS. 

Option (c) LHS: If there is an x such that α(x) is true, then β is true. RHS: For all the x, if α(x) is true, then β is true. LHS and RHS are the same because β is a formula with no free variable independent of x. (suppose if β is true for one x, it is true for all x and vice-versa). So, RHS⟹LHS and LHS⟹RHS. 

Option (d) RHS: For every x, if α(x) is true, then β is also true. So, RHS⟹LHS and LHS⟹̸ RHS; thus, option c is correct. because for option (c), LHS and RHS being equal, even if the implication reverses, it remains valid.

41. Which of the subsequent is the negation of? [Gate IT 2008]

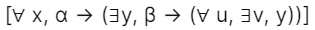
Answer: D

Explanation: While negating a quantified statement, we negate all the quantifiers first, from left to right (keeping order), then negative the statement. 
We can take examples as 
1. ¬[∀x ∈ A, P(x)] ⇔ ∃x ∈ A, ¬P(x). 
2. ¬[∃x ∈ A, P(x)] ⇔ ∀x ∈ A, ¬P(x). 
3. ¬[∀x ∈ A, ∃y ∈ B, P(x, y)] ⇔ ∃x ∈ A, ∀y ∈ B, ¬P(x, y). 
4. ¬[∃x ∈ A, ∀y ∈ B, P(x, y)] ⇔ ∀x ∈ A, ∃y ∈ B, ¬P(x, y).
Important, to negate an implication: ¬[IF P, THEN Q] ⇔ P AND NOT Q 
Now question is to negate this qualified statement: [∀ x, a -> (∃y, B -> (∀u, ∃v,y))] 
By negating it: ¬ [∀ x, a -> (∃y, B -> (∀u, ∃v,y))] ∃x, a ^ { ¬(∃y) , ¬[ B -> (∀u, ∃v,y) ] } ∃x, a ^ ( ∀y, B ^ ¬ (∀u, ∃v,y)) ∃x, a ^ ( ∀y, B ^ (∃u, ∀v, ¬y)) 
Option D is correct.

42. What is the converse of the below assertion? [GATE CS 1998]

Answer: A

Explanation: "I stay only if you go" is equivalent to "If I stay, you go."

 therefore, A only if B≡(A→B)∵A only if B≡(A→B)

A=A= "I stay" and B=B= "You go."

Converse (A→B)=B→A(A→B)=B→A

"If you go, then I stay."

So, the answer is (A).

43. Which of the subsequent propositions is a tautology? [GATE CS 1997]

A. (p ∨ q) → p

B. p ∨ (q → p)

C. p ∨ (p → q)

D. p → (p → q)

Answer: C

Explanation: A.  (p ∨ q) → p

≡ ¬(p ∨ q) ∨ p

≡ (¬p ∧ ¬q) ∨ p

≡ (¬p ∨ p) ∧ (¬q ∨ p)

≡ (p ∨ ¬q)

B.  p ∨ (q → p)

≡  p ∨ (¬q ∨ p)

≡ (p ∨ p) ∨ ¬q

≡ p ∨ ¬q

C.  p ∨ (p → q)

≡ p ∨ (¬p ∨ q)

≡ (p ∨ ¬p) ∨ q

≡ T ∨ q

≡ T 

D.  p → (p → q)

≡  p → (¬p ∨ q)

≡  ¬p ∨ (¬p ∨ q)

≡  (¬p ∨ ¬p) ∨ q

≡ ¬p ∨ q

Hence, Option(C) p ∨ (p → q).

44. Which of the following is false? Read ∧ as AND, ∨ as OR, ∼ as NOT, → as one-way implication, and ↔ as two-way implication. [GATE CS 1996]

A. ((x→y) ∧ x)→ y

B. ((∼x→y) ∧ (∼x→∼y))→ x

C. (x→ (x ∨ y))

D. ((x ∨ y) ↔ (∼x→∼y))

Answer: D

Explanation: A.  ((x → y) ∧ x) → y

≡  ¬((¬x ∨ y) ∧ x) ∨ y

≡  ((x ∧ ¬y) ∨ ¬x) ∨ y

≡  ((x ∨ ¬x) ∧ (¬x ∨ ¬y)) ∨ y

≡  (T ∧ (¬x ∨ ¬y)) ∨ y

≡  (¬x ∨ ¬y) ∨ y

≡  (y ∨ ¬y) ∨ ¬x

≡  T ∨ ¬x

≡  T

B.  ((¬x → y) ∧ (¬x → ¬y)) → x

≡  ¬((x ∨ y) ∧ (x ∨ ¬y)) ∨ x

≡  ((¬x ∧ ¬y) ∨ (¬x ∧ y)) ∨ x

≡  ((¬x ∧ (¬y ∨ y)) ∨ x

≡  (¬x ∧ T) ∨ x

≡  (¬x ∨ x)

≡  T

C.  (x → (x ∨ y))

≡  (¬x ∨ (x ∨ y))

≡  (¬x ∨ x) ∨ y

≡  T ∨ y

≡  T

D.  ((x ∨ y)⇔(¬x → ¬y))

≡  ((x ∨ y)⇔(x ∨ ¬y))

≡  ((x ∨ y)→(x ∨ ¬y))∧((x ∨ ¬y)→(x ∨ y))

≡  (¬(x ∨ y) ∨ (x ∨ ¬y)) ∧ (¬(x ∨ ¬y) ∨ (x ∨ y))

≡  ((¬x ∧ ¬y) ∨ (x ∨ ¬y)) ∧ (¬x ∧ y) ∨ ((x ∨ y))

≡  (((¬x ∧ ¬y) ∨ x)¬y) ∧ (((¬x ∧ y) ∨ x) ∨ y)

≡  (((¬x ∨ x) ∧ (x ∨ ¬y)) ∨ ¬y) ∧ (((¬x ∨ x) ∧ (x ∨ y)) ∨ y)

≡  ((T ∧ (x ∨ ¬y)) ∨ ¬y) ∧ ((T ∧ (x ∨ y)) ∨ y)

≡  ((x ∨ ¬y) ∧ (x ∨ y))

≡  (x ∧ x) ∨ (x ∧ y) ∨ (x ∧ ¬y) ∨ (¬y ∧ y)

≡  x ∨ (x ∧ y) ∨ (x ∧ ¬y)∨F

≡  x ∨ (x ∧ y) ∨ (x ∧ ¬y)

≡  x

Hence, Option(D). ((x ∨ y)⇔(¬x → ¬y))((x ∨ y)⇔(¬x → ¬y)).

45. Let apple(x) be a predicate that x is an apple, and Let green(x) be a predicate that the color of x is green. Which of the subsequent statements does not represent the given statement? [GATE CS Mock 2018]

"Not every apple is green."

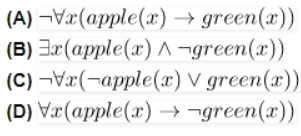
Answer: D

Explanation: Negation of the options are:

A: Not all apples are green.

B: There exists an apple that is not green.

C: Same as option A, with the implication expanded.

D: All apples are not green.

Therefore, the correct option is D.

46. How many given below logical equivalence(s) is/are false? [GATE CS Mock 2018]

(i)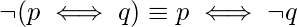

(ii)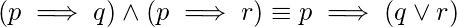

(iii)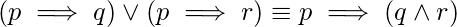

(iv)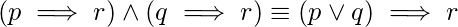

(v)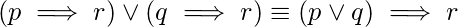

(A) 0

(B) 2

(C) 3

(D) None of these

Answer: C

Explanation: The correct logical equivalences are as:

(i)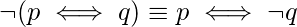

(ii)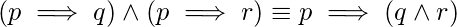

(iii)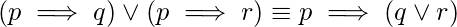

(iv)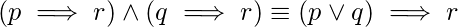

(v)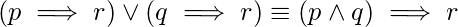

Hence, only equivalences (ii), (iii), and (v) are false.

So, the answer is 3.

47. What is the correct translation of the following statement into mathematical logic? [GATE CS Mock 2018]

“Every student who walks talks”

(I) ∀x ((student(x) & walk (x)) → talk (x)))

(II) ∀x (student(x) → (walk (x) → talk (x)))

(III)  ¬ ∃x ((student(x) & walk (x)) & ¬(talk (x))))

A. Only (I)

B. Only (II)

C. Only (II) and (III)

D. All (I), (II), and (III)

Answer: D

Explanation: All the above are correct & and equivalent to the first-order logic of the statement “Every student who walks talks”. Option (D) is correct.

48. Which of the following compound proposition is not a tautology? [GATE CS Mock 2018]

A. ((p → q) ∧ (q → r))→(p → r)

B. ((p ∧ q) ∧ (q ∧ r))→(p ∧ r)

C. ((p ⊕ q) ∧ (q ⊕ r))→(p ⊕ r)

D. (P V Q) Λ (P V R) → P V (Q Λ R)

Answer: C

Explanation: (A) ((p→q)∧(q →r))→(p→r) => pq' + qr' + p' + r = q'+ q + p' + r = True 

(B) ((p∧q)∧(q∧r))→(p∧r) => p' + q' + r' + pr = p' + q' + r' + r = True 

(C) ((p⊕q)∧(q⊕r)) → (p⊕r) is not a tautology as seen by the case where p and r are T and q is F or the case where p and r are F and q is T. 

(D) (P V Q) Λ (P V R) ≡ P V (Q Λ R) = (P V Q) Λ (P V R) → P V (Q Λ R) is true and its a distributive law. Option (C) is correct.

49. Consider these statements: 

Which of the following is/are false statement(s) about quantifiers? [GATE CS Mock 2018 | Set 2]

A. S2 and S3

B. S1 and S4

C. S1, S2, and S4

D. S2, S3, and S4

Answer: D

Explanation: By distributing quantifiers, we know that ∀ can be distributed over conjunction and ∃ disjunction. Therefore, S2, S3, and S4 are False. Option (D) is correct.

50. The binary operation c is defined as follows: 

Which one of the below is equivalent to P∨Q?

A)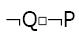

B)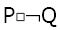

C)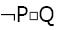

D)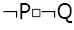

Answer: B

Explanation: PcQ = PQ + PQ' + P'Q'

        = P(Q + Q') + P'Q'

        = P(T) + P'Q'

        = P + P'Q'

        = (P + P')(P + Q')

        = T(P + Q')

        = P + Q'

Similarly, PcQ' = P + Q

Hence, option B is correct.

51. Consider the first-order logic sentence:

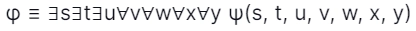
where ψ(s, t, u, v, w, x, y) is a quantifier-free first-order logic formula using predicate symbols solely and possibly equality, but no function symbols. Assume φ has a model with a universe containing seven elements. Which of the following statements is necessarily true? [GATE CS 2018]

Answer: A

Explanation: Let's interpret the problem this way: ∀ always True and always False for all empty sets. Thus, at least one model with a universe of size 3 (or less than). Therefore, option (A) is necessarily TRUE.

52. The following proposition is a? [ISRO CS 2017]

(P⇒Q) ⋀ (Q⇒P)

A. tautology

B. contradiction

C. contingency

D. absurdity

Answer: C

Explanation: 

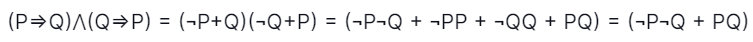
Hence a contingency.

53. Let T(x) denotes x is a trigonometric function, C(x) denotes x is a continuous function, and P(x) denotes x is a periodic function, then the statement 

can be logically represented as? [ISRO CS 2017]

A. ¬∃(x) [T(x) ⋀ ¬P(x)]

B. ¬∃(x) [T(x) ⋁ ¬P(x)]

C. ¬∃(x) [¬T(x) ⋀ ¬P(x)]

D. ¬∃(x) [T(x) ⋀ P(x)]

Answer: A

Explanation: Some trigonometric functions are not periodic = ∃(x) [ T(x) ⋀ ¬P(x) ] And it's negation is = ¬∃(x) [ T(x) ⋀ ¬P(x) ] Which is equivalent to "It is not the case that some trigonometric functions are not periodic" is equivalent to "All trigonometric functions are periodic" can be expression as = ∀(x) [T(x) → P(x)] = ∀(x) [¬ T(x) ⋁ P(x)] = ∀(x) ¬ [ T(x) ⋀ ¬P(x)] = ¬∃(x) [ T(x) ⋀ ¬P(x) ] 
Option (A) is correct.

54. Let P and Q be the two propositions, then ¬(P ↔ Q) is equivalent to [UGC-NET CS 2017 Nov - II]

(I) P ↔ ¬ Q (II) ¬ P ↔ Q (III) ¬ P ↔ ¬ Q (IV) Q → P

Answer: A

Explanation: We know that ¬(P ↔ Q) = (¬P ↔ Q) = (P ↔ ¬Q) = ¬(¬P ↔ ¬Q) Only statement (I) and (II) are correct. So, option (A) is correct.

55. Negation of the proposition ∃xH(x) is: [UGC-NET CS 2017 Dec 2]

A. ∃x¬H(x)

B. ∀x¬H(x)

C. ∀xH(x)

D. ¬xH(x)

Answer: B

Explanation: Since logic says that there exists some x for which H(x) is true, the negation for this will be for all x H(x) is not true. We can write it:

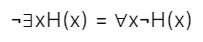
So, option (B) is correct.

56. Let P, Q, R, and S be some propositions. Suppose that P ⇔ (Q ∨ ¬ Q) and Q ⇔ R hold the equivalences. Then the truth value of the formula 

(P ∧ Q) ⇒ ((P ∧ R) ∨ S) 

is always? [UGC-NET CS 2017 Nov - III]

A. True

B. False

C. Same as truth table of Q

D. Same as truth table of S

Answer: A

57. “If X, then Y unless Z” is described by which of the following formulae in propositional logic? [UGC-NET CS 2017 Nov - III]

A. (X ∧ Y) → ¬ Z

B. (X ∧ ¬ Z) → Y

C. X → (Y ∧ ¬ Z)

D. Y → (X ∧ ¬ Z)

Answer: B

Explanation: If X then Y is represented by X → Y, one more condition is unless Z, we will include it in X, so X then Y, unless Z is expressed by (X ^ ¬Z) → Y. So, option (B) is correct.

58. Consider the subsequent two well-formed formulas in propositional logic.

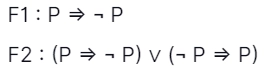
Which of the following statements is correct? [UGC-NET CS 2017 Nov - III]

A. F1 is Satisfiable, F2 is valid

B. F1 is unsatisfiable, F2 is Satisfiable

C. F1 is unsatisfiable, F2 is valid

D. F1 and F2 both are Satisfiable

Answer: A

Explanation: F1: P → ¬P = ¬P(¬P) + P¬(¬P) = ¬P + P is satisfiable. 
F2: (P ⇒ ¬ P) ∨ (¬ P ⇒ P) = (¬P(¬P) + P¬(¬P)) v (P¬(¬P) + ¬P(¬P) ) = satisfiable v satisfiable is satisfiable. 
So, option (A) is correct.

59. Which one of the below Boolean expressions is NOT a tautology? [ISRO CS 2017 - May]

A. ((a → b) ∧ (b → c)) → (a → c)

B. (a ↔ c) →( ¬b → (a ∧ c))

C. (a ∧ b ∧ c) → (c ∨ a)

D. a → (b → a)

Answer: B

Explanation: (A) a -> b means if ‘a’ is true, then ‘b’ is also true.

Now, ‘b’ is true. Therefore, ‘c’ is also true.

=> Using transitivity rule , a -> c

(B) a <-> c is true if both ‘a’ and ‘c’ have the same values.

Let ‘a’, ‘b,’ and c’ be false.

Expression ‘a and b‘ is false, and expression ‘not b’ is true.

RHS of the given equation should be true. But it evaluates to be false. Therefore, contradiction is there. Option (B) is not a tautology.

(C) Let ‘a’ and ‘c’ be false. ’b’ be true

a and b and c are false

c or a is false

(D) Let ‘b’ be true.

b -> a means if ‘b’ is true, then ‘a’ is also true.

Therefore, ‘a’ and ‘b’ are both true.

Hence, option (B) is correct.

60. In propositional logic, if 

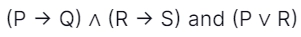
 are two premises, such that:

(P → Q) ∧ (R → S) 

P ∨ R 

Y 

Y is the premise : [UGC NET CS 2017 Jan - II]

A. P ∨ R

B. P ∨ S

C. Q ∨ R

D. Q ∨ S

Answer: D

Explanation: 

Given: 

(P → Q) ˄ (R → S)

(P ˅ R) 

If P then Q and R then S, P V R means either Q is true or S is true.

So, Y will be Q V S. Hence, option (D) is correct.