
Introduction
Propositional Logic transforms a complete sentence into a symbol. It makes it logical, whereas, in First-Order Logic, a particular sentence will be made that involves relations, functions, and constants. This article has popular propositional and first-order logic questions in past year gate exams.
Questions
61. ECL or emitter-coupled logic is the fastest of all logic families. High speed in ECL is possible because we use transistors in different amplifier configurations, in which they are never driven into ____. [UGC NET CS 2017 Jan - II ]
A. Race condition
B. Saturation
C. Delay
D. High impedance
Answer: B
62. Which of the subsequent statements is true? [UGC NET CS 2017 Jan - III]
Answer: B
63. The first-order logic (FOL) statement ((R ∨ Q) ∧ (P ∨ ¬Q)) is equivalent to which of the following? [UGC NET CS 2017 Jan - III]
A. ((R ∨ ¬Q) ∧ (P ∨ ¬Q) ∧ (R ∨ P))
B. ((R ∨ Q) ∧ (P ∨ ¬Q) ∧ (R ∨ P))
C. ((R ∨ Q) ∧ (P ∨ ¬Q) ∧ (R ∨ ¬P))
D. ((R ∨ Q) ∧ (P ∨ ¬Q) ∧ ( ¬R ∨ P))
Answer: B
Explanation: The FOL(first order logic) statement ((R ∨ Q) ∧ (P ∨ ¬Q)) is PR + ¬QR + PQ is equivalent to:
Option 1: ((R ∨ ¬Q) ∧ (P ∨ ¬Q) ∧ (R ∨ P)) is (R + ¬Q)(P + ¬Q)(R + P))
i.e. = RP + R¬Q +P¬Q not equivalent to PR + ¬QR + PQ.
Option 2: ((R ∨ Q) ∧ (P ∨ ¬Q) ∧ (R ∨ P)) is (R + Q)(P + ¬Q)(P + R)
i.e. = PR + ¬QR + PQ is exactly same.
Option 3: ((R ∨ Q) ∧ (P ∨ ¬Q) ∧ (R ∨ ¬P)) is (R + Q)(P + ¬Q)(R + ¬P)
i.e. = PR + ¬QR + R(P ↔ Q) not equivalent to PR + ¬QR + PQ.
Option 4: ((R ∨ Q) ∧ (P ∨ ¬Q) ∧ ( ¬R ∨ P)) is (R + Q)(P + ¬Q)(¬R + P)
i.e. = PR + PQ + P(Q → R) not equivalent to PR + ¬QR + PQ.
64. The Boolean expression [~(~p ∧ q) ∧ ~( ~p ∧ ~q)] ∨ (p ∧ r)] is equal to the Boolean function: [UGC NET CS 2016 Aug – II]
A. q
B. p ∧ r
C. p ∨ q
D. p
Answer: D
Explanation: We have Boolean expression: [~(~p ∧ q) ∧ ~( ~p ∧ ~q)] ∨ (p ∧ r)] = [(p ∨ ~q) ∧ (p ∨ q ) ∨ (p ∧ r)] = [p ∨ (p ∧ q) ∨ (p ∧ ~q) ∨(p ∧ r)] = p[1 ∨ q ∨ ~q ∨ r] = p So, option (D) is correct.
65. Let us assume that you construct ordered the tree to represent the compound proposition (~ (p ∧ q)) ↔ (~ p ∨ ~ q). Then, the prefix and postfix expressions determined using this ordered tree are given as ____ and _____, respectively. [UGC NET CS 2016 Aug – II]
A. ↔~∧pq∨ ~ ~ pq, pq∧~p~q~∨↔
B. ↔~∧pq∨ ~ p~q, pq∧~p~q~∨↔
C. ↔~∧pq∨ ~ ~ pq, pq∧~p~~q∨↔
D. ↔~∧pq∨ ~ p~ q, pq∧~p~ ~q∨↔
Answer: B
Explanation: We have compound proposition (~ (p ∧ q)) ↔ (~ p ∨ ~ q): Now we will construct ordered tree: We are asked to determine pre-order (i.e. parent-node left-node right-node), we will drive it from ordered tree i.e. ↔ ~ ∧ p q ∨ ~ p ~q And post-order(i.e. left-node right-node parent-node) from the ordered tree it is p q ∧ ~ p ~ q ~ ∨ ↔. So, option (B) is correct.
66. Let A and B set in a finite universal set U. Given the following: |A ⊕ B|, |A - B|, |A ∪ B| and |A| + |B| Which is in order of increasing size? [UGC NET CS 2016 Aug – II]
A. |A – B| < |A ⊕ B| < |A| + |B| < |A ∪ B|
B. |A ⊕ B| < |A – B| < |A ∪ B| < |A| + |B|
C. |A ⊕ B| < |A| + |B| < |A – B| < |A ∪ B|
D. |A – B| < |A ⊕ B| < |A ∪ B| < |A| + |B|
Answer: D
Explanation: |A – B| = |A| - |A ∩ B|
|A ⊕ B| = |A| + |B| - 2|A ∩ B|
|A ∪ B| = |A| + |B| - |A ∩ B|
Therefore,
|A – B| < |A ⊕ B| < |A ∪ B| < |A| + |B|
So, option (D) is correct
67. Let ν(x) mean x is a vegetarian, m(y) for y is meat, and e(x, y) for x eats y. Based on these, consider the following sentences: I. ∀x ν(x ) ⇔ (∀y e(x, y) ⇒ ¬m(y)) II. ∀xν(x) ⇔ (¬(∃y m(y) ∧e(x, y))) III. ∀x (∃ym(y) ∧e(x, y)) ⇔ ¬ν(x) One can determine that: [UGC NET CS 2016 Aug - III]
A. Only I and II are equivalent sentences.
B. Only II and III are equivalent sentences.
C. Only I and III are equivalent sentences.
D. I, II, and III are equivalent sentences.
Answer: D
Explanation: I. If x is vegetarian, then all the food items he eats must not include a meat item
II. If x is vegetarian, then there should not be at least one mean item that x eats
III. If there exists one meat item that x eats, then x is not a vegetarian
All these sentences are equivalent. Hence, option D is correct.
68. Consider the following logical inferences : I1: If school will not open if it is Sunday. The school was open. Inference: It was not Sunday. I2: If it is Sunday, then the school will not open. It was not Sunday. Inference: The school was open. Which of the following is correct? [UGC NET CS 2016 Aug - III]

Answer: B
Explanation: p: it is Sunday q: the school will open
So if it is Sunday, then the school will not open represented as:
p->~q so that it can imply q->~p (by contrapositive), so the first inference is correct for second.
If it is Sunday, then the school will not open represented as p->~q
given ~p, so it can not imply ~p->q (inverse implication) unless its converse(~q->p) is true, which is not true here.
Hence, option (B) is correct.
Note that only contrapositive holds true in all cases.
69. The negation of the following statement is? [UGC NET CS 2016 July – III]
“Either – 2 ≤ x ≤ – 1 or 1 ≤ x ≤2”. 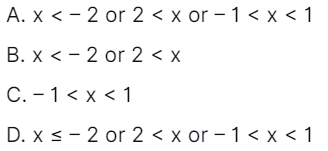
Answer: A
Explanation: “Either -2 ≤ x ≤ -1 or 1 ≤ x ≤ 2”. that is either x ≥ -2 or x ≤ -1 or 1 ≤ x or x ≤ 2”. To find negation of the statement: Negation of x ≥ -2 is x < 2, Negation of 1 ≤ x is x < 1, Negation of x ≤ -1 is x > -1, Negation of x ≤ 2 is x > 2. i.e. x < – 2 or 2 < x or – 1 < x < 1. Hence, option (A) is correct.
70. Which of the below are not valid arguments? [UGC NET CS 2015 Dec - II]


Answer: B
Explanation: Arguments (a) and (b) are not valid arguments.
If n is a real number, n>1, then n2>1. Suppose that n2>1, then n>1. This is a valid argument.
So, option (B) is correct.
71. Match the following terms: [UGC NET CS 2015 Dec - II]

- (1)
- (2)
- (3)
- (4)
Answer: A
Explanation: The vacuous proof is a proof in which the implication p → q is true because p is false.
- In trivial proof, the implication p → q is true based on the fact that q is true.
- In Direct proof, the implication p → q is true proceeds by showing that q must be true when p is true.
- In indirect proof, the implication p → q is true proceeds by showing that p must be false when q is false.
Hence, option (A) is correct.
72. Consider the following compound propositions as: (a)p ∨ ~(p ∧ q) (b)(p ∧ ~q) ∨ ~(p ∧ q) (c)p ∧ (q ∨ r) Which of the propositions are tautologies? [UGC NET CS 2015 Dec - II]
A. (a) and (c)
B. (b) and (c)
C. (a) and (b)
D. only (a)
Answer: D
Explanation:
- p ∨ ~(p ∧ q) = p + (pq)` = p + p` + q` = 1 + q` = 1, is a tautology.
- (p ∧ ~q) ∨ ~(p ∧ q) = pq` + (pq)` = pq` + p` + q` = p` + q`, is not a tautology.
- p ∧ (q ∨ r) = pq + pr, is NOT a tautology.
So, option (D) is correct.
73.


Answer: A
Explanation: "If my computations are valid and I pay the electric bill, I will run out of money.": if (c Λ b)→r "If I don't pay the electric bill, we will turn the power off. Hence, if I don't run out of money and the power is still on, my computations are incorrect.": (¬r Λ p)→¬c. So, option (A) is correct.
74. Match the following: [UGC NET CS 2015 Jun - II]

- (1)
- (2)
- (3)
- (4)
Answer: A
Explanation:
- (p → q) ⇔ (¬q → ¬p) is Contrapositive.
- [(p ∧ q) → r] ⇔ [p → (q → r)] is exportation law.
- (p → q) ⇔ [(p ∧ ¬q) → o] is Reductio ad absurdum.
- (p ↔ q)⇔[(p → q)∧(q → p)] is Equivalence.
So, option (A) is correct.
75. Suppose a proposition is given as “ x ≥ 6, if x2 ≥ 5 and it's proof as If x ≥ 6, then x2 = x.x ≥ 6.6 = 36 ≥ 25. Which of the below are correct w.r.t. the given proposition and its proof? [UGC NET CS 2015 Jun - II]


Answer: C
Explanation: "x ≥ 6 if x2 ≥ 5 and it's proof as If x ≥ 6, then x2 = x.x ≥ 6.6 = 36 ≥ 25. It is clear from these statements that proof begins by assuming what is to be shown, and it is clear that the proof demonstrates the converse of what is to be proved; hence the proof is not correct. Statements (a) and (b) are correct, but (3) statement is not correct. Hence, option (C) is correct.
76. A horn clause is ___________. [UGC NET CS 2015 Dec – III]

Answer: D
Explanation: In logic programming, the horn clause has at most one positive literal. When there is exactly one positive literal, it is known as a definite clause, but it is called a goal clause when there is no positive literal. So, option (D) is correct.
77. In the Propositional Logic, given P and P → Q, we can infer __________. [UGC NET CS 2015 Dec – III]
A. ~ Q
B. Q
C. P ∧ Q
D. ~ P ∧ Q
Answer: B
Explanation: The rule of inference logic states that if a conditional statement (‘if p then q’) is valid, and the antecedent (p) holds (i.e., P and P → Q), then we may infer the consequent (q). Option Q is correct.
78. Which of the following is false for the PROLOG programming language? [UGC NET CS 2015 Jun - III]

Answer: B
Explanation: Regarding PROLOG, the statement "PROLOG is a strongly typed language" is False, among others. Hence, option (B) is correct.
79. Which one of the subsequent is true? [UGC NET CS 2015 Jun - III]

Answer: B
Explanation: The statement "The resolvent of two Horn clauses is a Horn clause." is true. So, option (B) is correct.
80. In the propositional logic, P ↔ Q is equivalent to which of the following (Where ~ denotes NOT): [UGC NET CS 2015 Jun - III]
A. ~( P ∨ Q ) ∧ ~ ( Q ∨ P )
B. ( ~P ∨ Q ) ∧ (~ Q ∨ P )
C. ( P ∨ Q ) ∧ ( Q ∨ P )
D. ~( P ∨ Q ) → ~ ( Q ∨ P )
Answer: B
Explanation: P ↔ Q = (P → Q) ∧ (Q → P)
P ↔ Q = (~P ∨ Q) ∧ (~Q v P)
So, option (B) is correct.
81. Determine the correct translation into the logical notation of the subsequent assertion.

Note: taller (x, y) is true if x is taller than y. [GATE-CS-2004]
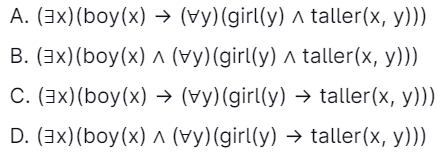
Answer: D
Explanation: Many people get confused about when to use ∧ and when to use →. This question tests precisely that.
We use ∧ when we want to say that both predicates in this statement are always true, no matter the value of x.
We use → when we want to say that although there is no need for the left predicate always to be true, the right predicate must also be true whenever it becomes true.
D means there exist some boys x which taller than all girls y.
82. Equivalent logical expression for the WFF(Well Formed Formula), ~(∀x) F[x]. [UGC NET CS 2014 Dec - III]
A. ∀x (~F[x])
B. ~(∃x) F[x]
C. ∃x (~F[x])
D. ∀x F[x]
Answer: C
Explanation: ~ (∀x) F(x)
= (∃x)(~F(x))
So, option (C) is correct.
83. The resolvent to the set of the clauses (A ∨ B, ~A ∨ D, C ∨ ~B) is: [UGC NET CS 2014 Dec - III]
A. A ∨ B
B. C ∨ D
C. A ∨ C
D. A ∨ D
Answer: B
Explanation: C ∨ D
A∨B, ∼A∨D, C∨∼B
A and ∼A will cancel out, and so will B and ∼B.
Hence, option (B) is correct.
84. Consider the English sentence: “Agra and Gwalior are both in India.” A student has written a logical sentence for the above English sentence in First-Order Logic using the predicate In(x, y), which means x is in y, as follows: In(Agra, India) ∨ In(Gwalior, India). Which one of the subsequent is correct concerning the above logical sentence? [UGC NET CS 2018 July - II]

Answer: A
Explanation: In (Agra, India) means Agra is in India.
In (Gwalior, India) means Gwalior is in India.
In(Agra, India) ∨ In(Gwalior, India), here "∨" means "or". So the entire gives the meaning of Either Agra is in India or Gwalior is in India. Hence, the statement does not express the meaning of the English sentence, and option (A) is correct.
85. The equivalence of ¬∃x Q(x) is: [UGC NET CS 2018 July - II]
A. ∃x ¬Q(x)
B. ∀x ¬Q(x)
C. ¬∃x ¬Q(x)
D. ∀x Q(x)
Answer: B
Explanation: This is a simple property for negating Quantified,
¬∃x Q(x) = ∀x ¬Q(x)
Hence, option (B) is correct.
86. Which of the following predicate formulae is NOT logically valid? Remember that W is a predicate formula without any free occurrence of x. [GATE CS 2020]
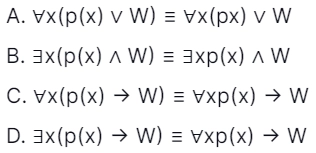
Answer: C
Explanation: ∀x (p(x) → W) ≡ ∀xp(x) → W is wrong. Since ∀x [p(x) → W]
≡ ∀x [¬p(x) ∨ W]
≡ ∀x (¬p(x) ∨ W
≡ ¬(∃x p(x)) ∨ W
≡ ∃x p(x) → W
Hence, option (C) is correct.
87. Which one of the following is the main conjunctive normal form for [(pVq) ∧ ~p → ~q]? [NTA UGC NET 2019 June - II]
A. pV~q
B. pVq
C. ~pVq
D. ~pV~q
Answer: A
Explanation:

88. Match List-I with List-II [NTA UGC NET 2019 June - II]

Choose the correct option from the following:
A. a-ii, b-iii, c-i, d-iv
B. a-ii, b-i, c-iii, d-iv
C. a-iv, b-i, c-iii, d-ii
D. a-iv, b-iii, c-i, d-ii
Answer: B
Explanation:





