Introduction
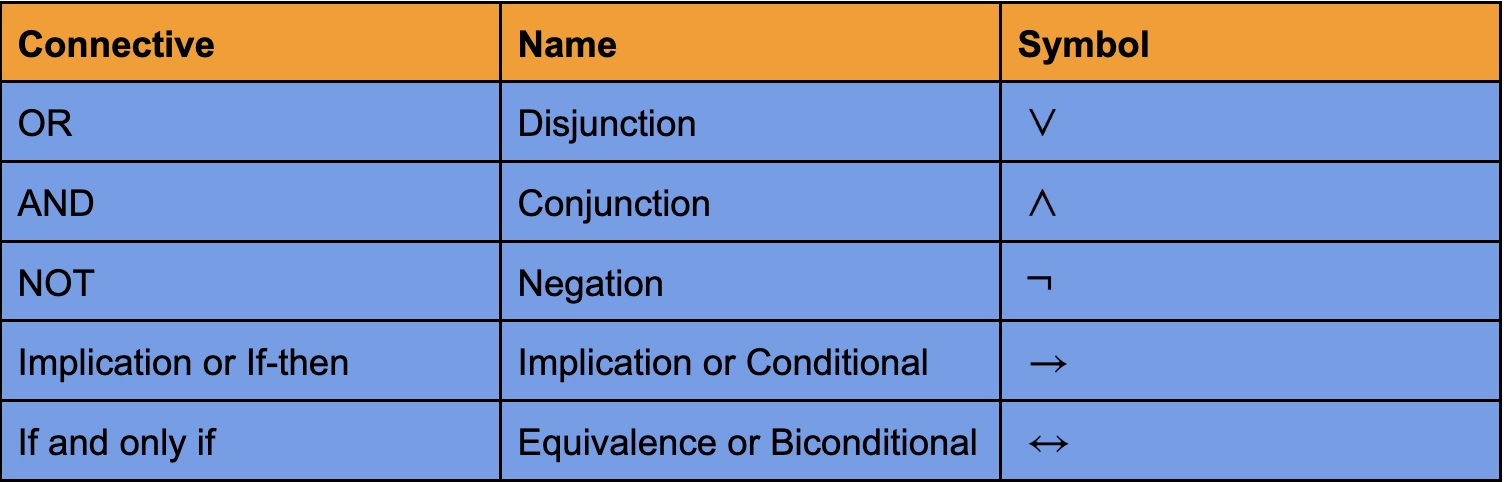
Mathematical logic principles define how to reason about mathematical statements. Aristotle, a Greek philosopher, is credited with inventing logical reasoning. It has numerous applications in computer science, including the design of computing devices, artificial intelligence, and the construction of data structures for programming languages, among others.
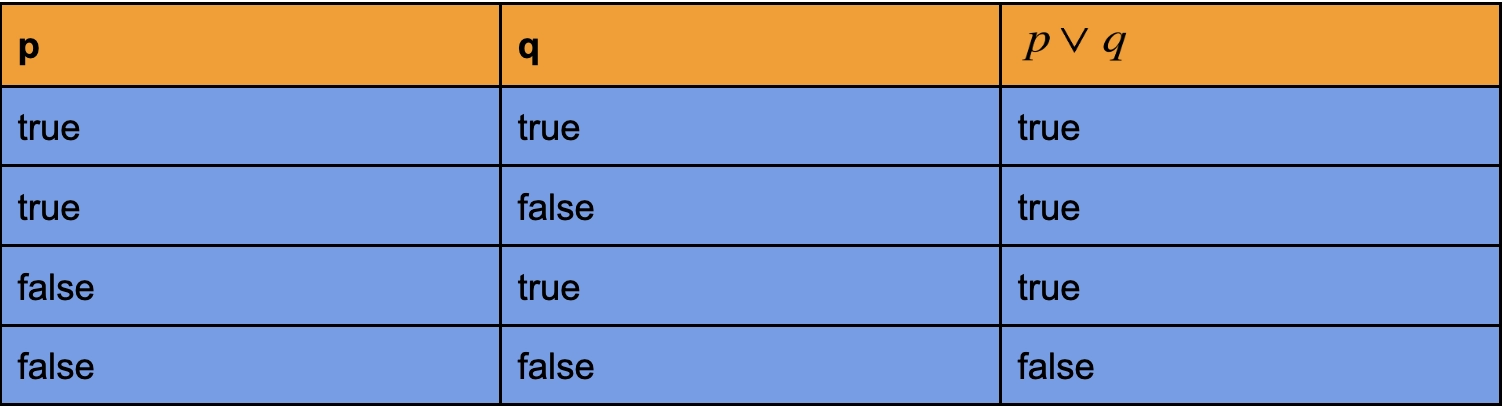
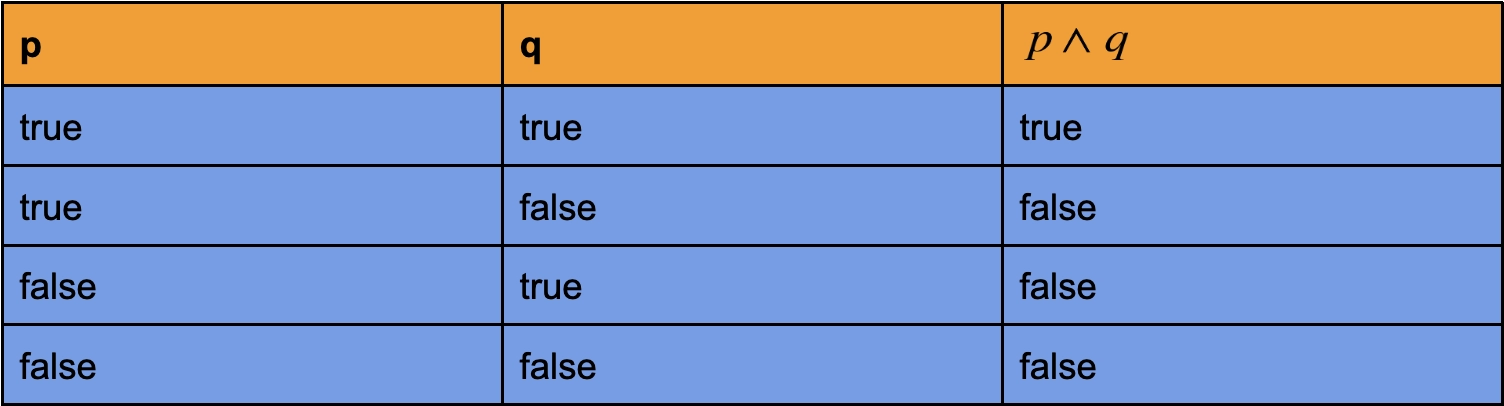
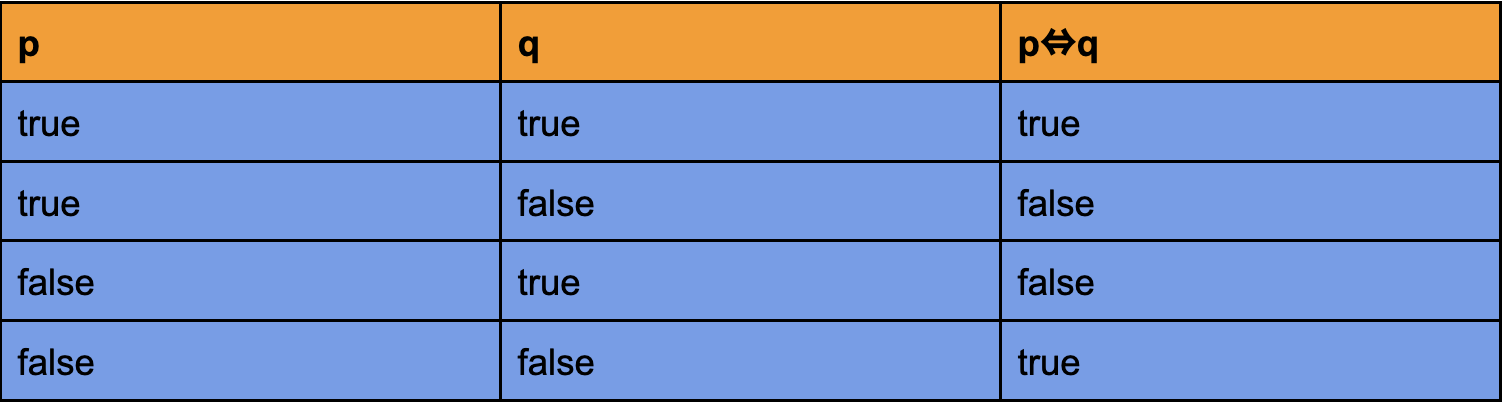
Propositional logic concerns statements that can be assigned the truth values true and false. The goal is to evaluate these statements individually and as a group.
Let’s learn about these propositions and compound statements in-depth.
Proposition
A proposition is a set of declarative statements with the truth value true or false attached to them. Propositional variables and connectives make up a propositional.
Examples of propositions are given below:-
Examples:
1.) If x is an integer, then its square is positive.
2.) 12 + 9 = 8 + 13, it will return true.
3.) 25*10 = 5*100, it will return false.
Examples that are not propositions are given below:-
Examples:
1.) What is your name?
2.) X is less than 5.
The above two examples are not propositions because we cannot prove that they are true or false.
Propositional Variables
Variables used to represent propositions are known as Propositional Variables.
Usually, the propositions are represented by lower case letters beginning with p.
Examples:
p: Delhi is the capital of India.
q: 5 + 5 = 10