Example
Let m be the length of the Prufer code. The goal is to make a graph with m+2 vertices that are empty. The first element is removed from the sequence. Let x be the first element in the current sequence. Then we look for the most negligible value that isn't in the supplied sequence and hasn't been added to the tree yet. Let's call this value y. We repeat this step by adding an edge from x to y. Let's look at the algorithm for building a tree using the example:
Input: (3, 1, 4, 3)
Step 1: We start by making an empty graph with six vertices and extracting four from the sequence.
Step 2: Of the 1 through 6 vertices, 2 is the one that is not in the Prufer sequence.
Step 3: We make a dividing line between 2 and 4.
1 3 5 6
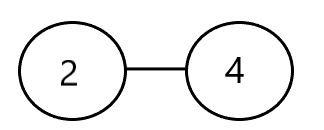
Step 4: The next vertex in the sequence is 1, and the matching vertex with the least degree is 5 (since 2 has already been taken into account).
2—---4 1—----5 3 6

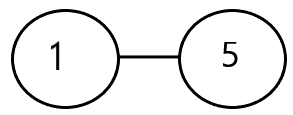
Step 5: The number 3 comes next in the sequence, and the associated vertex with the least degree is 1. (as 1 is now not part of the remaining Prufer sequence)
6

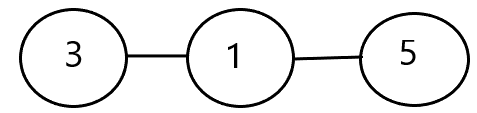
Step 6: The next vertex in the sequence is 4, and the corresponding vertex with the least degree is 3 (since 3 is not present further in the sequence).
6

Step 7: Finally, from 1 to 6, two vertices (4 and 6) are missing, so we link them.
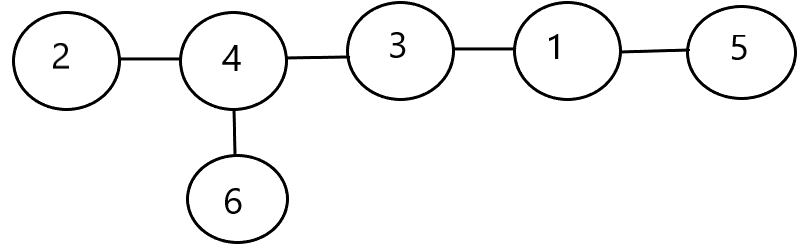
This tree is the six-vertices tree that is necessary.
Source Code
We see the algorithm of prufer code in detail. Now below is the program source code of Prufer code to tree creation in different programming languages.
Java
public class Main
{
static void displayTreeEdges(int prufer[])
{
int vertex = prufer.length + 2;
int v_set[] = new int[vertex];
for (int i = 0; i < vertex - 2; i++)
v_set[prufer[i] - 1] += 1;
System.out.print("\nThe edge set E(G) is :\n");
// Find the smallest label not present in
// prufer[].
int j = 0;
for (int i = 0; i < vertex - 2; i++) {
for (j = 0; j < vertex; j++) {
if (v_set[j] == 0) {
System.out.print("(" + (j + 1) + ", " + prufer[i] + ") ");
v_set[j] = -1;
v_set[prufer[i] - 1]--;
break;
}
}
}
j = 0;
// For the last element
for (int i = 0; i < vertex; i++) {
if (v_set[i] == 0 && j == 0) {
System.out.print("(" + (i + 1) + ", ");
j++;
}
else if (v_set[i] == 0 && j == 1)
System.out.print((i + 1) + ")\n");
}
}
// Driver code
public static void main(String args[])
{
int prufer[] = { 5, 1, 2, 4, 3 };
displayTreeEdges(prufer);
}
}

You can also try this code with Online Java Compiler
Output:-
The edge set E(G) is :
(6, 5) (5, 1) (1, 2) (2, 4) (4, 3) (3, 7)

You can also try this code with Online Java Compiler
C++
#include <iostream>
using namespace std;
void printTreeEdges(int prufer[])
{
int size = sizeof(prufer) / sizeof(prufer[0]);
int vertex = size + 2;
int v_set[vertex];
for (int i = 0; i < vertex; i++)
v_set[i] = 0;
for (int i = 0; i < vertex - 2; i++)
v_set[prufer[i] - 1] += 1;
cout << "\nThe edge set E(G) is :\n";
int j = 0;
for (int i = 0; i < vertex - 2; i++) {
for (j = 0; j < vertex; j++) {
// If j+1 not present in prufer set
if (v_set[j] == 0) {
// Remove from Prufer set and print
the pair.
v_set[j] = -1;
cout << "(" << (j + 1) << ", "
<< prufer[i] << ") ";
v_set[prufer[i] - 1]--;
break;
}
}
}
j = 0;
// For the last element
for (int i = 0; i < vertex; i++) {
if (v_set[i] == 0 && j == 0) {
cout << "(" << (i + 1) << ", ";
j++;
}
else if (v_set[i] == 0 && j == 1)
cout << (i + 1) << ")\n";
}
}
// Driver code
int main()
{
int prufer[] = { 5, 1, 2, 4, 3 };
printTreeEdges(prufer);
return 0;
}

You can also try this code with Online C++ Compiler
Output:-
The edge set E(G) is :
(6, 5) (5, 1) (1, 2) (2, 4) (4, 3) (3, 7)

You can also try this code with Online C++ Compiler
Python
def printTreeEdges(prufer):
vertex = len(prufer) + 2
v_set = [0] * vertex
for i in range(vertex - 2):
v_set[prufer[i] - 1] += 1
print("The edge set E(G) is :")
# Find the smallest label not present in
# prufer.
j = 0
for i in range(vertex - 2):
for j in range(vertex):
# If j+1 not present in prufer set
if (v_set[j] == 0):
# Remove from Prufer set and print
the pair.
v_set[j] = -1
print("(" , (j + 1),", ",prufer[i],") ",sep = "",end = "")
v_set[prufer[i] - 1] -= 1
break
j = 0
# For the last element
for i in range(vertex):
if (v_set[i] == 0 and j == 0):
print("(", (i + 1),", ", sep="", end="")
j += 1
elif (v_set[i] == 0 and j == 1):
print((i + 1),")")
# Driver code
prufer = [5, 1, 2, 4, 3 ]
printTreeEdges(prufer)

You can also try this code with Online Python Compiler
Output:-
The edge set E(G) is :
(6, 5) (5, 1) (1, 2) (2, 4) (4, 3) (3, 7 )

You can also try this code with Online Python Compiler
Time complexity: O(N log N)
where N is the number of vertices.
Frequently Asked Questions
What is the purpose of the prufer code?
The Prüfer sequence (also Prüfer code or Prüfer numbers) of a labeled tree is a unique sequence associated with the tree in combinatorial mathematics. A simple iterative approach can construct the sequence for a tree with n vertices of length n-2.
What is a tree data structure in Java?
A tree is a non-linear data structure that organizes data elements according to their hierarchical relationships. The structure is non-linear because data in a tree is not organized linearly, unlike Arrays, Linked Lists, Stacks, and Queues.
What exactly is a labeled tree?
A labeled tree is one in which each vertex has been assigned a distinct label. The labels 1, 2,..., n are commonly assigned to the vertices of a labeled tree with n vertices.
Conclusion
In this article, we have extensively discussed the prufer code to tree creation in different programming languages.
Check out this problem - XOR Queries On Tree
We hope this blog has helped you enhance your knowledge regarding prufer code.
If you would like to learn more, check out our articles on Tree in Java, Binary Tree, and N-ary Trees. Practice makes a man perfect. To practice and improve yourself in the interview, you can check out Top 100 SQL problems, Interview experience, Coding interview questions, and the Ultimate guide path for interviews.
Do upvote our blog to help other ninjas grow. Happy Coding!











