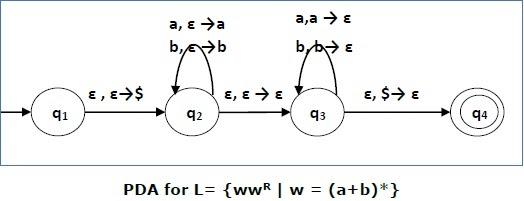
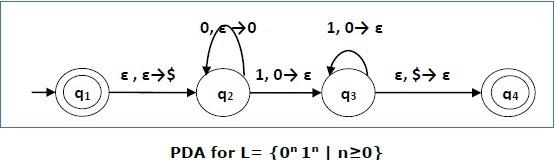
Introduction
A pushdown automaton (PDA) is a computational model that recognizes context-free languages. It consists of an input tape, a stack, and a finite set of states. The PDA transitions between states based on input symbols and stack operations, which allows it to parse and validate strings generated by context-free grammars. In this article, we will discuss pushdown automata in detail.

A Pushdown Automata (PDA) can be defined as :
- Q is the set of states
- ∑is the set of input symbols
- Γ is the set of pushdown symbols (which can be pushed and popped from stack)
- q0 is the initial state
- Z is the initial pushdown symbol (which is initially present in the stack)
- F is the set of final states
Also See, Moore Machine
PDA Components:
1. Input Tape:
- A read-only tape that contains the input string to be processed by the PDA.
- The input string is a sequence of symbols from the input alphabet.
- The PDA reads the input string from left to right, one symbol at a time.
2. Stack:
- A last-in-first-out (LIFO) data structure used for storing and manipulating symbols.
- The stack has an alphabet of stack symbols, which can be pushed onto or popped from the top of the stack.
- The stack is used to store information and make decisions based on the stored information.
3. States:
- A finite set of states that represent the different configurations of the PDA.
- The PDA transitions between states based on the current input symbol and the top symbol of the stack.
- There is a designated start state where the PDA begins its computation.
- There are also one or more final states (also called accept states) that indicate successful processing of the input string.
4. Transition Function:
- A set of rules that define how the PDA moves from one state to another based on the current input symbol and the top symbol of the stack.
- The transition function specifies the next state, the symbol to be pushed onto the stack (if any), and the symbol to be popped from the stack (if any).
- The transition function can be represented as a transition table or a set of transition rules.
5. Input Alphabet:
- A finite set of symbols that the input string can consist of.
- The input alphabet is used to define the valid symbols that can appear on the input tape.
6. Stack Alphabet:
- A finite set of symbols that can be stored on the stack.
- The stack alphabet includes a special symbol (usually denoted as Z) that represents the bottom of the stack.
7. Acceptance Condition:
- The criteria that determine whether the PDA accepts or rejects an input string.
- The PDA accepts an input string if it reaches a final state after consuming all the input symbols and the stack is empty.
- If the PDA cannot reach a final state or the stack is not empty after consuming all the input symbols, the input string is rejected.