What is a segment tree??

A segment tree is a type of data structure that is used to store information about intervals or array segments. Using it, we can efficiently handle update and range queries. It can be stored using an array.

Is a segment tree a binary tree?

In a segment tree, every node except leaf nodes has two children, left and right. Therefore, it is a complete binary tree.

Why is the build function's time complexity O(N)?

There are 2 * N - 1 node in a segment tree, and while building, we process each node once, so the overall time complexity is O(N).

Table of contents

Problem Statement

1.1.

Constraints

1.2.

Sample Test Cases

Approach

Code

3.1.

Input

3.2.

Output

Complexity

4.1.

Time Complexity

4.2.

Space Complexity

FAQs

Key Takeaways

Last Updated: Mar 27, 2024

Queries to calculate sum of squares of array elements over range of indices [L, R] with updates

Author Abhishek Ranjan

Problem Statement

Given an integer array A of size N, handle Q queries of the following types:

(0, l, r, x): Replace all the elements in the subarray A[l],[l + 1]......A[r - 1],A[r] with x.
(1, l, r, x): Increment all the elements in the subarray A[l],[l + 1]......A[r - 1],A[r] by x.
(2, l, r): Calculate sum of squares of elements in the subarray A[l],[l + 1]......A[r - 1],A[r].

Constraints

1 <= N, Q <= 5e5
1 <= l , r <= N
1 <= x <= 1e6

Sample Test Cases

Input:	8 5
 		1 2 3 4 5 6 7 8
 		2 1 3
  		0 1 4 4
        2 1 3
        1 1 8 1
        2 1 5

Output: 14
		48
		136
Explanation: Initially, A = {1, 2, 3, 4, 5, 6, 7, 8}
Query1: The sum of squares of all the elements in the range [1, 3] = 1 * 1 + 2 * 2 + 3 * 3 = 1 + 4 + 9 = 14.

Query2: Replace all the elements in the range [1, 4] with 4,
      A = {4, 4, 4, 4, 5, 6, 7, 8}

Query3: The sum of squares of all the elements in the range [1, 3] = 4 * 4 + 4 * 4 + 4 * 4 = 16 + 16 + 16 = 48. 

Query4: Increment all the elements in the range [1, 8] by 1,
      A = {5, 5, 5, 5, 6, 7, 8, 8}

Query5: The sum of squares of all the elements in the range [1, 8] = 5 * 5 + 5 * 5 + 5 * 5 + 5 * 5 + 6 * 6 = 25 + 25 + 25 + 25 + 36 = 136.

Also see, Euclid GCD Algorithm

Approach

We can solve this problem efficiently using the segment tree with lazy propagation.

To answer the query, we will maintain a segment tree that stores the sum of squares in a range, and to perform the update, along with the lazy tree, we need another segment tree that will store the sum of elements in a range.

Instead of creating two segment trees, we can create one that will store two variables, the 'sum' (to store the sum) and the 'sumOfSquare' (to store the sum of squares).

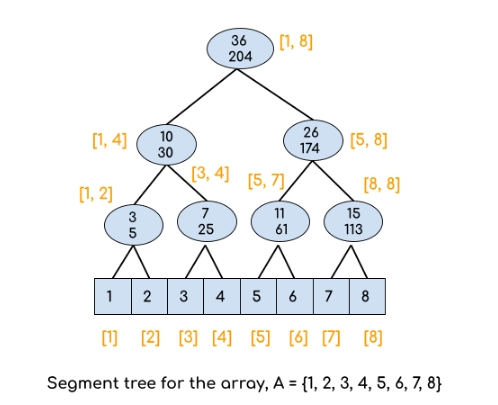
How to perform the update in the range [l, r]??

To update all the elements lying in the range [l, r], we will start from the root node and recursively update the nodes in the following way -

Suppose [cl, cr] be the range of the current node. Now there are 3 cases:

cr < l or cl > r: The current node is out of range, so there is no need to update it or its children.
cl >= l and cr <= r: The current node lies entirely inside the range [l, r], so update it and postpone the update of its children using the lazy tree.
(cl < l and cr <= r) or (cl >= l and cr > r): The current node overlaps partially. So recursively update its children first then update it.

In the case of the first type of update (0, l, r, x):

The updated sum is ,

sum = a[l] + a[l + 1] + ..... + a[r - 1] + a[r]

= x + x + ... + x

= (cr - cl + 1) * x

and the updated sum of square is,

sumOfsquare = a[l] * a[l] + a[l + 1] * a[l + 1] + ..... + a[r - 1] * a[r - 1] + a[r] * a[r]

= x * x + x * x + ......+ x * x + x * x

= (r - l + 1) * x * x

And,

In the case of the second type of update (1, l, r, x):

The updated sum is ,

sum = (a[l] + x) + (a[l + 1] + x) + ..... + (a[r - 1] + x) + (a[r] + x)

= (a[l] + a[l + 1] + ..... + a[r - 1] + a[r]) + (x + x + .... + x + x)

= sum + (r - l + 1) * x

and the updated sum of square is,

sumOfsquare = (a[l] + x)^2 + (a[l + 1] + x)^2 + + ..... + (a[r - 1] + x)^2 + (a[r] + x)^2

using the formula (p + q)^2 = p^2 + q^2 + 2 * p * q

sumOfsquare = a[l] * a[l] + a[l + 1] * a[l + 1] + ........ + a[r - 1] * a[r] + (x * x + x * x + ...... + x * x + x * x) + 2 * x * (a[l] + a[l + 1] + .... ... + a[r - 1] + a[r])

sumOfsquare = sumOfsquare + (r - l + 1) * x * x + 2 * x * sum

How to postpone the updates using the lazy tree??

Every node in the lazy tree stores two values, 'type' and 'val'. type = -1 indicates that there is no pending update, type = 0 indicates pending update of type (0, l, r, x), and type = 1 indicates pending update of type (1, l, r, x).

Suppose lazy[] be an array used to store the lazy tree and node be the current node.

If the pending update at the current node (node) is of type 1, then perform the update using the above formulas and push the update to the children (i.e., set lazy[2 * node + 1] = lazy[node] and lazy[2 * node + 2] = lazy[node]).

If the update is of type 2, then update the current node using the above formulas. And to push the update to the children, there are two cases -

If there is no pending update (i.e lazy[2 * node + 1].type == -1): postpone the update at the current node to its children.
If there is a pending update (i.e lazy[2 * node + 1].type == 0 or lazy[2 * node + 1].type == 1): increment the val of children by val of the current node.

Code

#include <bits/stdc++.h>
using namespace std;
const int M = 200007;
//struct to store sum and sum of square of all the elements in the segment tree
struct TreeNode{
   int sum;
   int sumOfSquare;
   TreeNode(){
       sum = 0;
       sumOfSquare = 0;
   }
};
//struct for lazy tree
struct LazyNode{
   int type;
   int val;
   LazyNode(){
       type = -1;
       val = 0;
   }
};
//array to store segment tree
TreeNode segTree[4 * M];
//array to store lazy tree
LazyNode lazy[4 * M];
//function to update the values in the segment tree using the the values of lazy tree
void push(int node, int &st, int &en){
   if(lazy[node].type == -1)
       return;
   if(lazy[node].type == 0){
       segTree[node].sum = (en - st + 1) * lazy[node].val;
       segTree[node].sumOfSquare = (en - st + 1) * lazy[node].val * lazy[node].val;
       lazy[2 * node + 1] = lazy[node];
       lazy[2 * node + 2] = lazy[node];
   }
   else{
       segTree[node].sumOfSquare += (en - st + 1) * lazy[node].val * lazy[node].val + 
                                     2 * lazy[node].val * segTree[node].sum;
       segTree[node].sum += (en - st + 1) * lazy[node].val;
       if(lazy[2 * node + 1].type == -1){
           lazy[2 * node + 1] = lazy[node];
       }
       else{
           lazy[2 * node + 1].val += lazy[node].val;
       }
       if(lazy[2 * node + 2].type == -1)
           lazy[2 * node + 2] = lazy[node];
       else
           lazy[2 * node + 2].val += lazy[node].val;
   }
   lazy[node].type = -1;
}
//query function
int query(int node, int cl, int cr, int l, int r){
   push(node, cl, cr);
   if(cr < l || cl > r)
       return 0;
   if(cl >= l and cr <= r){
       return segTree[node].sumOfSquare;
   }
   int mid = (cl + cr)/2;
   int x = query(2 * node + 1, cl, mid, l, r);
   int y = query(2 * node + 2, mid + 1, cr, l, r);
   return x + y;
}
//update function
void update(int node, int cl, int cr, int l, int r, int type, int val){
   push(node, cl, cr);
   if(cr < l || cl > r)
       return;
   if(cl >= l and cr <= r){
       lazy[node].type = type;
       lazy[node].val = val;
       push(node, cl, cr);
   }
   else{
       int mid = (cl + cr)/2;
       update(2 * node + 1, cl, mid, l, r, type, val);
       update(2 * node + 2, mid + 1, cr, l, r, type, val);
       segTree[node].sum = segTree[2 * node + 1].sum + segTree[2 * node + 2].sum;
       segTree[node].sumOfSquare = segTree[2 * node + 1].sumOfSquare + segTree[2 * node + 2].sumOfSquare; 
   }
}
//build function to construct the segment tree
void build(int node, int st, int en, int a[]){
   if(st == en){
       segTree[node].sum = a[st];
       segTree[node].sumOfSquare = a[st] * a[st];
       return;
   }
   int mid = (st + en)/2;
   build(2 * node + 1, st, mid, a);
   build(2 * node + 2, mid + 1, en, a);
   segTree[node].sum = segTree[2 * node + 1].sum + segTree[2 * node + 2].sum;
   segTree[node].sumOfSquare = segTree[2 * node + 1].sumOfSquare + segTree[2 * node + 2].sumOfSquare;
}

int main(){
   int N, Q;
   //size, query
   cin >> N >> Q;
   //given array
   int a[N + 1];
   for(int i = 1; i <= N; ++i)
       cin >> a[i];
   //build the segment tree
   build(1, 1, N, a);
   while(Q--){
       int type;
       cin >> type;
       //update
       if(type == 0 || type == 1){
           int l, r, x;
           cin >> l >> r >> x;
           //function call
           update(1, 1, N, l, r, type, x);
       }
       //query
       else{
           int l, r;
           cin >> l >> r;
           //function call
           cout << query(1, 1, N, l, r) << "\n";
       }
   }
}

Input

8 5
1 2 3 4 5 6 7 8
2 1 3
0 1 4 4
2 1 3
1 1 8 1
2 1 5

Output

14
48
136

Complexity

Time Complexity

As we are using two extra arrays to store the segment tree and the lazy tree, the space complexity is O(N).

Space Complexity

As we are using two extra arrays to store the segment tree and the lazy tree, the space complexity is O(N).

FAQs

What is a segment tree??
A segment tree is a type of data structure that is used to store information about intervals or array segments. Using it, we can efficiently handle update and range queries. It can be stored using an array.
Is a segment tree a binary tree?
In a segment tree, every node except leaf nodes has two children, left and right. Therefore, it is a complete binary tree.
Why is the build function's time complexity O(N)?
There are 2 * N - 1 node in a segment tree, and while building, we process each node once, so the overall time complexity is O(N).

Key Takeaways

In this article, we solved a problem using the segment tree data structure with lazy propagation. The Segment tree is a very flexible data structure, and we can use it to solve a huge number of problems. Check out this coding ninjas' blog for getting a better hold on it.

Check out the following problems -

To learn more about such data structures and algorithms, Coding Ninjas Studio is a one-stop destination. This platform will help you to improve your coding techniques and give you an overview of interview experiences in various product-based companies by providing Online Mock Test Series and many more benefits.

Happy learning!