Queries to Count Array Elements from a Given Range having a Single Set Bit

Approaches

Brute force approach

In this approach for each query of 1st type, we will iterate through the range and will increase the count if the current element is having a single set bit i.e. the power of 2.

For 2nd type query, we will update the element of the given index with the given value.

Code

#include<bits/stdc++.h>
using namespace std;

//function to find the count of numbers having single set bit for a given range

int singleBit(vector<int> arr,int l,int r)
{
int count=0;
for(int i=l;i<=r;i++)
   {
    //if the number is power of 2
    if((arr[i] & (arr[i]-1))==0) {
        count++;
        }

   }
    return count;
}

//function for updating the array

void update(vector<int>& arr,int idx,int val)
{
arr[idx]=val;
}

//driver code

int main()
{
vector<int> arr{ 10, 9, 16, 2, 32 };

//queries
vector<vector<int>> Q{ { 1, 0, 3 },
                            { 2, 2, 20 },
                            { 1, 1, 4 } };
                            
    for (int i = 0; i < (int)Q.size(); i++) 
    {
    
     if(Q[i][0]==1)
        {
         cout<<singleBit(arr,Q[i][1],Q[i][2])<<endl;
}
else
{
update(arr,Q[i][1],Q[i][2]);
}
}
}

Output

Complexity

The above approach takes O(q*n) time in the worst case where q is the number of queries and n is the size of the given array.

Optimized approach using segment tree

For this approach, we will take the help of segment tree to solve this query problem more efficiently.

First, we need to build segment tree st[ ] from the given array. Each node of this segment tree will store the count of elements having a single set bit for a range of arr[], the node representing.

• Define a function buildST( ) with parameters idx,low,high. st[idx] stores the count of elements having single set bit for the range [low,high].

• if there is one element in the segment i.e low=high, the node st[idx] stores 1 if the current number is having a single set bit.

• if there is more than one element in the range, recur for left and right subtrees.
• updating the current node with total count of numbers having single set bit for left and right subtree i.e st[idx]=st[2*idx+1]+st[2*idx+2]

For 1st type of query define a function singleBit( idx, low, high, l, r).

• if the current segment [low,high] denoted by node at idx is part of the given range [l,r], return value of st[idx].
• If the segement [low,high] denoted by node at idx is ouside of the given range [l,r], return 0.
• if the given range overlaps with the segment of the current node, recur for the left and right subtree.

For 2nd type of query to update value at index idx, define update(idx,val,low,high,si).

• If low=high and idx=low, the current node is the leaf node of the segment tree. So, st[si] stores 1 if the current number is having a single set bit.

• Otherwise search for idx . If idx<=mid, traverse to left subtree update(idx,val,low,mid,2*si+1). Else traverse to right subtree by calling update(idx,val,mid+1,high,2*si+2).

Code

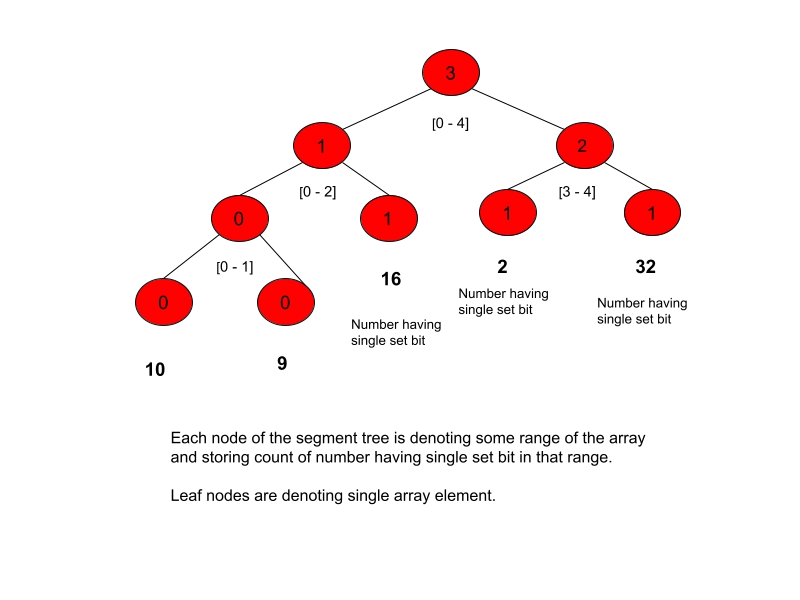
// c++ code implementation

#include<bits/stdc++.h>
using namespace std;

// constructing segment tree from the given array 

void buildST(int idx, int low,int high,vector<int> &st,int arr[])
{
// if there is one element in the array
if(low==high)
{
//the node stores 1 if the number is having single set bit
st[idx]=((arr[low] & (arr[low]-1))==0)?1:0;
return;
}

// if there is  more than one element,
// recur for left and right subtrees

int mid=(high+low)/2;

buildST(2*idx+1,low,mid,st,arr);
buildST(2*idx+2,mid+1,high,st,arr);

//updating current node with count of numbers having single set bit for [low,high] range
 st[idx]=st[2*idx+1]+st[2*idx+2];
}

// function to find count of numbers having single set bit for a given range[l,r]
int singleBit(int idx,int low,int high,int l,int r,vector<int> st)
{
// if the segment of node at idx is part of
// the given range 
if(l<=low && r>=high)
{
return st[idx];
}

// the segment of node at idx is ouside of the given range
if(high<l || low>r) return 0;

//if the given range overlaps with the segment of the current node

int mid=(high+low)/2;

int left=singleBit(2*idx+1,low,mid,l,r,st);
int right=singleBit(2*idx+2,mid+1,high,l,r,st);

return (left+right);
}

void update(int idx,int val,int low,int high,int si,vector<int>& st,int arr[])
{
if(low==high)
{
if(low==idx)
{
arr[idx]=val;
//the node stores 1 if the number is having single set bit
st[si]=((arr[idx] & (arr[idx]-1))==0)?1:0;

}
return;
}

//mid of the segement [low,high]
int mid=(high+low)/2;

if(idx<=mid)
{
update(idx,val,low,mid,2*si+1,st,arr);
}
else
{
update(idx,val,mid+1,high,2*si+2,st,arr);
}


//updating current node with count of numbers having single set bit for [low,high] range
st[si]=st[2*si+1]+st[2*si+2];
}

// Driver code

int main()
{
int n=5;

int arr[]={10, 9, 16, 2, 32 };

vector<int> st(2*n-1); // array representation of segment tree

buildST(0,0,n-1,st,arr);


//queries
vector<vector<int>> Q{ { 1, 0, 3 },
                            { 2, 2, 20 },
                            { 1, 1, 4 } };
                            
    for (int i = 0; i < (int)Q.size(); i++) 
    {
    
     if(Q[i][0]==1)
        {
         cout<<singleBit(0,0,n-1,Q[i][1],Q[i][2],st)<<endl;
}
else
{
update(Q[i][1],Q[i][2],0,n-1,0,st,arr);
}
}

}

Output

Complexity

The time complexity of the above approach O(n*log n + q*log n) where (nlogn) is time for constructing segment tree and (q*log n) is the time required for q queries.

Space complexity is O(n) as extra space is used for constructing a segment tree.

FAQs

1. What is a segment tree?
   A segment tree is a special kind of data structure that is used to store information about intervals or segments of an array. It can be represented by an array.
    
2. What kind of problem can be solved efficiently using a segment tree?
   A segment tree is used to solve min, max, or sum queries for a given range on an array as well as update queries in O(log n) time where n is the size of the array.

Key Takeaways

This article covered how to count array elements from a given range having a single set bit. We have seen the brute force approach as well as segment tree implementation.

To know more about the segment tree you can go through the articles of Coding Ninjas Studio library.

Check out this problem - Duplicate Subtree In Binary Tree

Side by side, you can also practice a wide variety of coding questions commonly asked in interviews in Coding Ninjas Studio. Along with coding questions, you can also find the interview experience of scholars working in renowned product-based companies here. 

Happy learning!