What is a segment tree?

A segment tree is a special kind of data structure that is used to store information about intervals or segments of an array. It can be represented by an array.

hat kind of problem can be solved efficiently using segment tree?A segment tree is used to solve min, max, or sum queries for a given range on an array as well as update queries in O(log n) time where n is the size of the array.

Table of contents

Introduction

Problem statement

Approach

Code

FAQs

Key Takeaways

Last Updated: Mar 27, 2024

Queries to Find The First Array Element Exceeding K with Updates

Author Malay Gain

Introduction

Finding the first array element exceeding K is not a very difficult task. By just array traversal we can find the required answer. But here we will implement an efficient approach to solve this problem. If we take the brute force approach, it will take O(q*n) time for q such queries. Here we will solve the problem efficiently using a segment tree.

Problem statement

There is an array of integers. You are given some queries of format {1,k} to find the first array element exceeding k (i.e. greater or equal to the value k) and some queries of format {2,i,val} to update the array element at ith index with val.

Input

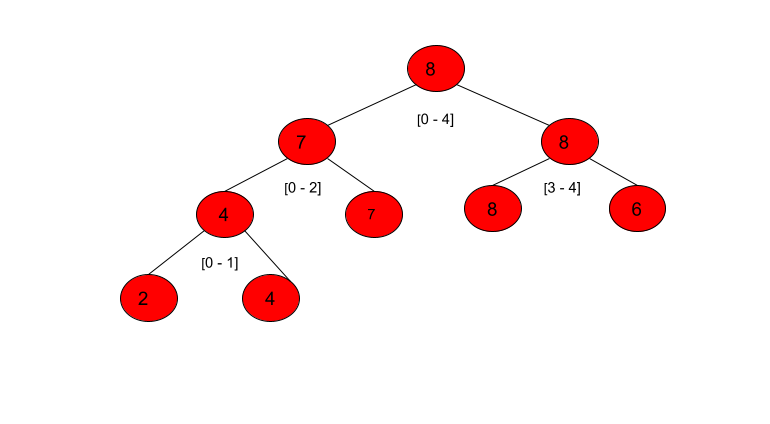
arr[ ] = {2, 4, 7, 8, 6}

Q= { { 1, 5 }, { 2, 3, 5 }, { 1, 4 }, { 1, 8 } }

Output

-1

Explanation

arr[ ]= {2, 4, 7, 8, 6}

0 1 2 3 4(indices)

So, for the {1,5} query we need to find the index of the first element exceeding 5 i.e. 2 as arr[2]=7.

Updated array after the query { 2, 3, 5 }; arr[ ]= {2, 4, 7, 5, 6}

Similarly, the output of the {1,4} query is 1.

As the updated array doesn’t contain any value exceeding 8, the output of the {1,8} query is -1.

Note: Please try to solve the problem first and then see the below solution approach.

Also see, Euclid GCD Algorithm

Approach

Here we will construct a segment tree st following the same way as range minimum query problem. The only difference for this case is instead of minimum, each node will store the maximum of its subtrees.

To find first array element exceeding k, we will define a function findMinIndex(idx,low,high,k,st)

Recursively check if the root of the left subtree is greater than or equal to k. If condition satisfied find the minimum index of the array element from the left subtree.
Otherwise check in the right subtree and recursively find the position.
If not found return MAX_INT.

For update operation, define a function update(idx,val,low,high,si) to update value at index idx with val.

If idx is less than or equal to the mid of the range [low,high], traverse to left subtree update(idx,val,low,mid,2*si+1). Otherwise, raverse to right subtree by calling update(idx,val,mid+1,high,2*si+2)

When low=high, we are at a leaf node of the segment tree which denotes idx of the given array. Update the value of the node st[low] as well as arr[idx].

Code

// c++ code implementation for finding the first array element exceeding K with updates

#include<bits/stdc++.h>
using namespace std;

// constructing segment tree from the given array 

void buildST(int idx, int low,int high,vector<int> &st,int arr[])
{
// if cuurent node is leaf
if(low==high)
{

st[idx]=arr[low];
return;
}

// if there is  more than one element,
// recur for left and right subtrees

int mid=(high+low)/2;

buildST(2*idx+1,low,mid,st,arr);
buildST(2*idx+2,mid+1,high,st,arr);

//updating current node with max of [low,high] range
st[idx]=max(st[2*idx+1],st[2*idx+2]);
}

// function for finding the index of the first array element exceeding K 
int findMinIndex(int idx,int low,int high,int k,vector<int> st)
{
//if no such eleemnt found
if(st[idx]<k)
{
return INT_MAX;
}

//if current node is leaf
if(low==high)
{
//if current node is greater or equal to k
if(st[idx]>=k)
{
return low;
}

return INT_MAX;
}

int ans=INT_MAX;

int mid=(high+low)/2;
//if root of the left subtree is greater or equal to k
if(st[2*idx+1]>=k)
    {
     ans=min(ans,findMinIndex(2*idx+1,low,mid,k,st));
}

//if no such index found in left subtree
if(ans==INT_MAX && st[2*idx+2]>=k)
{
ans=min(ans,findMinIndex(2*idx+2,mid+1,high,k,st));
}

return ans;
}

void update(int idx,int val,int low,int high,int si,vector<int>& st,int arr[])
{
if(low==high)
{

//update value in array
arr[idx]=val;
//update in segement tree
st[si]=val;


return;
}

//mid of the segement [low,high]
int mid=(high+low)/2;

if(idx<=mid)
{
update(idx,val,low,mid,2*si+1,st,arr);
}
else
{
update(idx,val,mid+1,high,2*si+2,st,arr);
}


//updating current node with count of numbers having single set bit for [low,high] range
st[si]=max(st[2*si+1],st[2*si+2]);
}

//driver code

int main()
{
int n=5;

int arr[]= {2, 4, 7, 8, 6};//{10, 9, 16, 2, 32 };

vector<int> st(2*n-1); // array representation of segment tree

buildST(0,0,n-1,st,arr);


//queries
vector<vector<int>> Q{ { 1, 5 }, { 2, 3, 5 }, { 1, 4 }, { 1, 8 } };
                            
    for (int i = 0; i < (int)Q.size(); i++) 
    {
    
     if(Q[i][0]==1)
        {
         int ans=findMinIndex(0,0,n-1,Q[i][1],st);
         cout<<(ans<n?ans:-1)<<endl; // print -1 if no such element exceeding k found
        }
else
{
update(Q[i][1],Q[i][2],0,n-1,0,st,arr);
}
}

}

Output

-1

Complexity

Time complexity of the above approach O(n*log n + q*log n) where (nlogn) is time for constructing segment tree and (q*log n) is the time required for q queries.

Space complexity is O(n) as extra space is used for constructing a segment tree.

Check out this problem - First And Last Occurrences Of X

FAQs

What is a segment tree?
A segment tree is a special kind of data structure that is used to store information about intervals or segments of an array. It can be represented by an array.
What kind of problem can be solved efficiently using segment tree?
A segment tree is used to solve min, max, or sum queries for a given range on an array as well as update queries in O(log n) time where n is the size of the array.

Key Takeaways

This article covered how to find the first array element exceeding K with updates using segment tree.

To know about more about segment tree you can go through the articles of Coding Ninjas Studio library.

Side by side, you can also practice a wide variety of coding questions commonly asked in interviews in Coding Ninjas Studio. Along with coding questions, you can also find the interview experience of scholars working in renowned product-based companies here.

Happy learning!

Live masterclass

Land an SDE Role at Google: Master DSA the smart way

by Saurav Prateek, SDE2@Google

19 Sep, 2024

01:30 PM

38+ registered

Become a Data Analyst at MAANG: Learn PowerBI for Data visualization

by Megna Roy, Senior Data Analyst @Amazon

17 Sep, 2024

01:30 PM

281+ registered

Learn Advanced Excel: Ace Data Analytics Interview

by Megna Roy, Data Analyst @ Amazon

15 Sep, 2024

06:30 AM

3864+ registered

Land an SDE Role at Google: Master DSA the smart way

by Saurav Prateek, SDE2@Google

19 Sep, 2024

01:30 PM

38+ registered

Become a Data Analyst at MAANG: Learn PowerBI for Data visualization

by Megna Roy, Senior Data Analyst @Amazon

17 Sep, 2024

01:30 PM

281+ registered

View more events