
Introduction
Sorting plays a significant role, especially when giving a coding contest or appearing in an interview. Whether it’s an array or a linked list, some problems can be solved in less time if the data or elements are sorted because you know finding the solution is not enough; you should also optimize it if possible.
In this blog, we will cover how Quicksort works on a Linked list.
Also see, Data Structures and Rabin Karp Algorithm
What is a linked list?
It is a commonly used data structure that contains a linear collection of data whose order is not defined by their physical address in the memory. In this, each node (element) points towards the other. And depending on which way they point, different types of linked lists are created.
The different types of a linked list are:
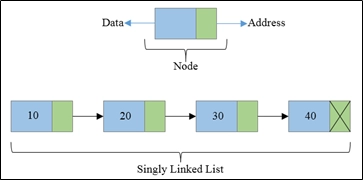
a) Singly Linked List: Node points towards the next node.
b) Doubly Linked List : Node points towards nodes on either side.
c) Circular Linked List: Last node points towards the first node, creating a circular path.
Note: Any node achieves the “pointing” by storing the node it wants to point towards.
In this session, we will talk about Quicksort on a Singly Linked List. Hence you must be able to recreate a diagram about singly linked list in your head, which looks as follows:
Quick Sort Algorithm
As the name suggests, Quicksort is a sorting algorithm that is one of the most popular and highly efficient sorting algorithms. It is faster compared to other algorithms as it uses the concept of divide and conquers, i.e., it continuously divides the given list into two parts, hence sending lower value items on one side and higher values on the other (depending on the need of the user).
Working on Quicksort Algorithm
Let’s understand the algorithm of Quicksort on a Singly Linked list first:
STEP 1. Take the last element on the list, and let’s call it PIVOT.
STEP 2. Now, take two halves, H for higher and L for lower elements.
STEP 3. Increase L while List[L] < PIVOT
STEP 4. Decrease H till the List[H] < PIVOT, then stop.
STEP 5. If H < L, then exchange, List[H], and List[L].
STEP 6. Repeat 3, 4 and 5 till H > L.
STEP 7. Exchange PIVOT element and List[H]Let’s understand the Quicksort pseudo-code:
- We are given an input array
- Choose pivot, here we are choosing the mid element as our pivot
-
Now we’ll partition the array as per the pivot
- Keep a partitioned index say p and then initialize it to -1
- Iterate through every element present in the array except the pivot
- If found an element that is less than the pivot element then increment p and swap the elements present at index p with the element at index i.
- Once traversing all the elements, swap pivot with element present at p+1 as this will be the same position as in the sorted array
- Now return the pivot index
-
Once partitioned, now make 2 calls on quicksort
- One from beg to p-1
-
Other from p+1 to n-1
Quicksort Algorithm:-
quickSort(arr, beg, end)
if (beg < end)
pivotIndex = partition(arr,beg, end)
quickSort(arr, beg, pivotIndex)
quickSort(arr, pivotIndex + 1, end)
partition(arr, beg, end)
set end as pivotIndex
pIndex = beg - 1
for i = beg to end-1
if arr[i] < pivot
swap arr[i] and arr[pIndex]
pIndex++
swap pivot and arr[pIndex+1]
return pIndex + 1
E.g. In the given image below, we can see how Quicksort works on an array:-
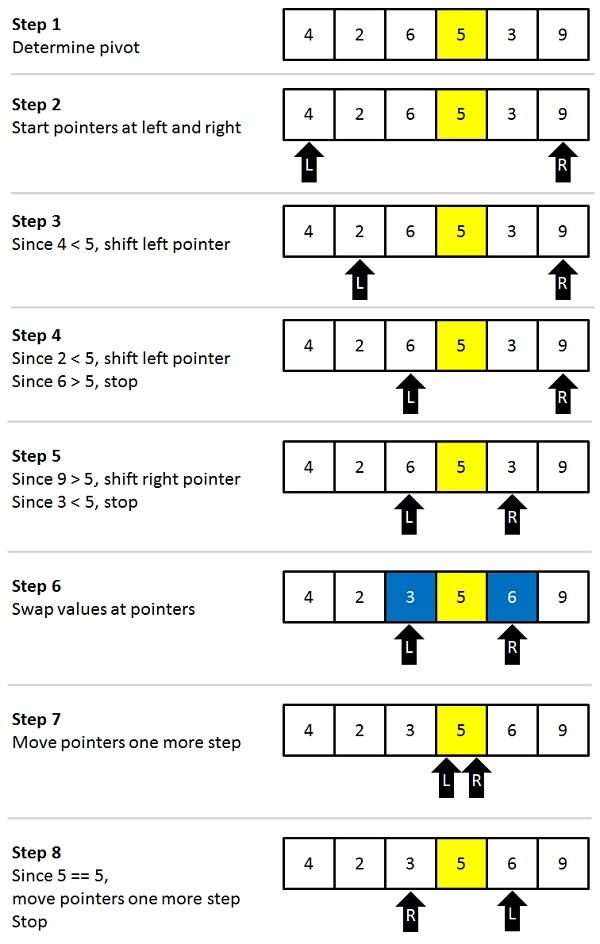
In the given image above we can see we chose element 5 as a pivot and we will start by keeping two pointers approach with the first element of the array as left and the last element of the array as right. And we’ll start comparing since the algorithm is based on if the element on the left side of the pivot is greater than the right side of the element then we’ll swap till the time we reach the pivot element.
Implementation of Quicksort on a Singly Linked List in Java
public class QuickSortLinkedList {
static class Node {
int data;
Node next;
Node(int d)
{
this.data = d;
this.next = null;
}
}
Node head;
void addNode(int data)
{
if (head == null) {
head = new Node(data);
return;
}
Node curr = head;
while (curr.next != null)
curr = curr.next;
Node newNode = new Node(data);
curr.next = newNode;
}
void printList(Node n)
{
while (n != null) {
System.out.print(n.data);
System.out.print(" ");
n = n.next;
}
}
// Initiate the first and the last node without breaking any links in the whole linked list.
Node partitionLast(Node start, Node end)
{
if (start == end || start == null || end == null)
return start;
Node pivot_prev = start;
Node curr = start;
int pivot = end.data;
// Iterate till pen-ultimate node, since the last node is the PIVOT
while (start != end) {
if (start.data < pivot) {
pivot_prev = curr;
int temp = curr.data;
curr.data = start.data;
start.data = temp;
curr = curr.next;
}
start = start.next;
}
// swap whichever is following suitable index and pivot
int temp = curr.data;
curr.data = pivot;
end.data = temp;
return pivot_prev;
}
void sort(Node start, Node end)
{
if(start == null || start == end|| start == end.next )
return;
// split list and partition recurse
Node pivot_prev = partitionLast(start, end);
sort(start, pivot_prev);
// If PIVOT = START, we pick from next of PIVOT.
if (pivot_prev != null && pivot_prev == start)
sort(pivot_prev.next, end);
// If PIVOT is still in between the list, start from next to pivot since we have pivot_prev, so we move two nodes.
else if (pivot_prev != null
&& pivot_prev.next != null)
sort(pivot_prev.next.next, end);
}
// Main Driver Code
public
static void main(String[] args)
{
QuickSortLinkedList list = new QuickSortLinkedList();
list.addNode(10);
list.addNode(1);
list.addNode(2);
list.addNode(8);
list.addNode(5);
Node n = list.head;
while (n.next != null)
n = n.next;
System.out.println("Linked List before sorting");
list.printList(list.head);
list.sort(list.head, n);
System.out.println("\nLinked List after sorting");
list.printList(list.head);
}
}
Output:
Linked List before sorting
10 1 2 8 5
Linked List after sorting
1 2 5 8 10 Time Complexity: O(N^2) in the worst case, where N is the number of elements in the linked list and O(N*logN) in the average case.
Auxiliary Space: O(1), as we are not using any additional space.





