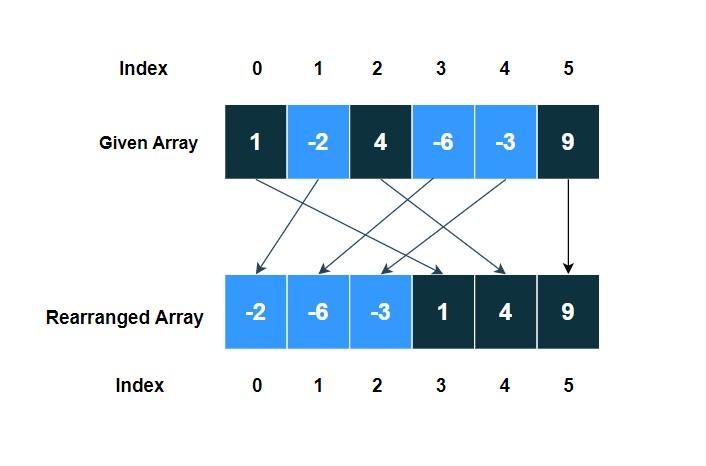
Solution(Using Merge Sort technique)
Here, we will try to solve the problem using the Merge Sort technique. If you don’t know how mergesort works, follow the article Merge Sort first. Implement Merge Sort in Coding Ninjas Studio.
Idea
Here, we will use the idea of the Merge Sort. Merge Sort follows divide and conquer algorithms. It first divides the array into two halves, then compares them, and updates the initial array accordingly.
The idea for this case is as follows:
- Continue dividing the array into two halves until we are left with a single element.
- Arrange the element in each half so that all negative elements appear before the positive elements by keeping their order.
- Follow the above procedure for all possible halves.
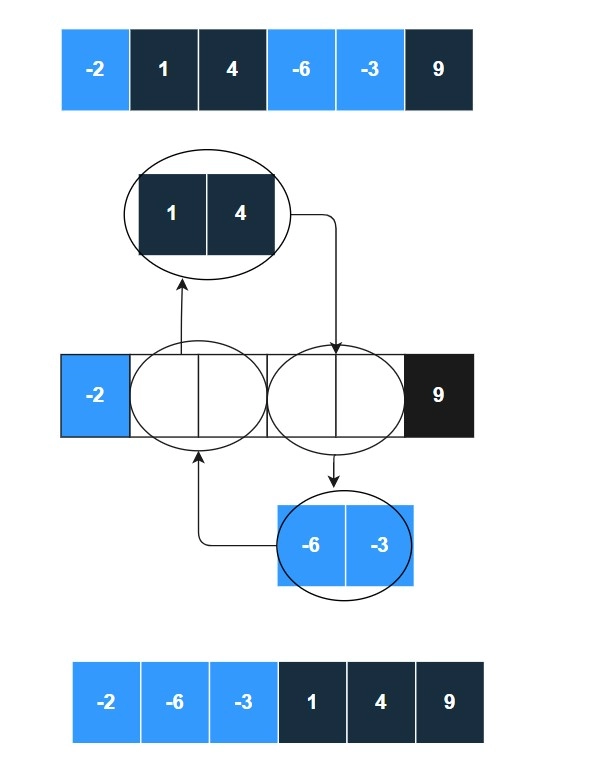
Visualisation
Let’s visualise the above idea using the sample test case.
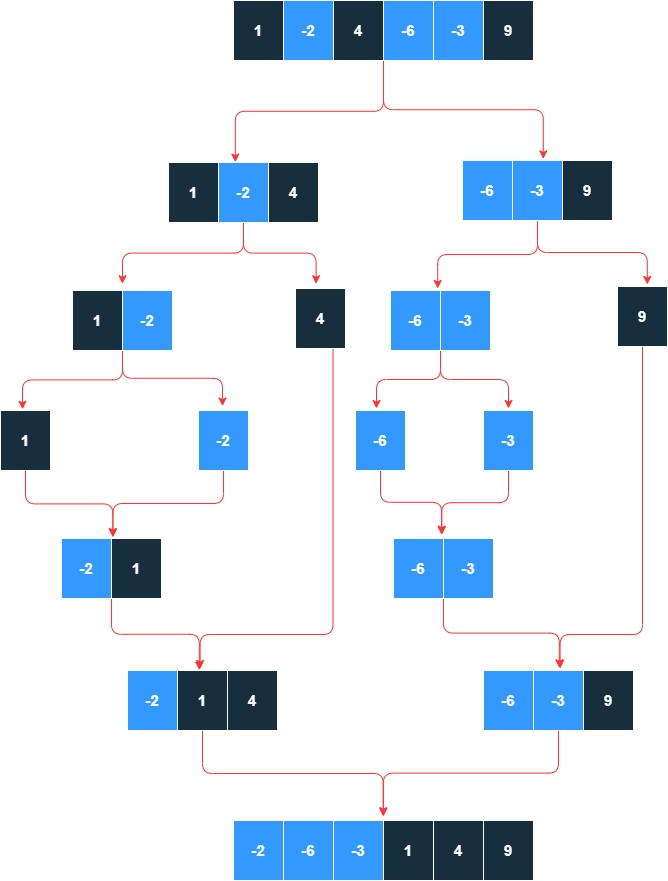
We can code the above algorithm using extra space and without using any extra space.
For better understanding, we first implement the above idea using extra space.
Code in C++(Using Extra Space)
#include<bits/stdc++.h>
using namespace std;
// merge sort technique
void merge(int arr[] , int lo , int mid , int hi) {
// size of the left half
int left_half_size = mid - lo + 1;
// size of the right half
int right_half_size = hi - mid;
// left_half array
int left_half[left_half_size];
// right_half array
int right_half[right_half_size];
// store the values of the left half in the left_half array
for(int i = lo ; i <= mid ; i++) {
left_half[i - lo] = arr[i];
}
// store the values of the right half in the right_half array
for(int i = mid + 1 ; i <= hi ; i++) {
right_half[i - mid - 1] = arr[i];
}
// here, we are modifying the subarray [lo, hi]
int p = lo;
// To keep the negative elements before all the positive elements by keeping the order same
// first store all the negative elements in the left_half in the original array
for(int i = 0 ; i < left_half_size ; i++) {
if(left_half[i] < 0) {
arr[p] = left_half[i];
p++;
}
}
// then store all the negative elements in the right_half in the original array
for(int i = 0; i < right_half_size ; i++) {
if(right_half[i] < 0) {
arr[p] = right_half[i];
p++;
}
}
// then store all the positive element of the left_half in the original array
for(int i = 0; i < left_half_size ; i++) {
if(left_half[i] > 0) {
arr[p] = left_half[i];
p++;
}
}
//finally, store all the positive elements of the right_half in the original array
for(int i = 0 ;i < right_half_size ; i++) {
if(right_half[i] > 0) {
arr[p] = right_half[i];
p++;
}
}
}
void divide(int arr[] , int lo , int hi) {
// continue divinng the array into two parts repeatedly until lo == hi(we are left with a single element)
if(lo < hi) {
int mid = lo + (hi - lo) / 2;
divide(arr , lo , mid);
divide(arr , mid + 1 , hi);
merge(arr , lo , mid , hi);
}
}
void Rearrange(int arr[], int n)
{
// calling the divide method
divide(arr , 0, n - 1);
}
int main() {
// given array
int arr[] = {1 , -2 , 4 , -6, -3, 9};
// calculate size of the array
int n = sizeof(arr) / sizeof(arr[0]);
// call the function
Rearrange(arr , n);
// print the result
cout << "Resulting array is: ";
for(int i = 0 ; i < n; i++) {
cout << arr[i] <<" ";
}
}

You can also try this code with Online C++ Compiler
Output
Resulting array is: -2 -6 -3 1 4 9
Code Explanation
- First, we call the Rearrange(arr,n) function from the main function.
- Now control goes to Rearrange(arr,n) function.
- Rearrange function calls divide(arr,lo,hi) function.
- divide(arr,lo,hi) function is a recursive function, which repeatedly calls itself until we are left with a single element (lo == hi). Otherwise it divides the array into two halves [lo , mid] and [mid + 1, hi].
- After that, we call the merge(arr, lo, mid, hi) function to merge these two halves [lo, mid] and [mid + 1, hi] to update the sub-array arr[lo, hi].
- Inside the merge(arr, lo, mid, hi) we first store the left part [lo , mid] inside the left_half[] array and right part [mid + 1, hi] inside the right_half[] array.
- Then we start updating the original array arr[lo, hi].
- To store all negative elements before all positive elements, we first need to keep all the negative elements of these two arrays and then the positive elements.
- To keep the order of the negative element, we first store all the negative elements of the left_half and then store all the negative elements of the right_half. The same goes for the positive elements.
Complexity Analysis
Time Complexity: O(nlogn)
Space Complexity: O(n)
Where n = size of the array.
Now, let’s implement the above idea without using any extra space.
Optimisation in Space
If you carefully notice the above visualisation of the mergeSort implementation(see the above visualisation part once). You will be able to see a pattern in each of the two halves.
Observe the above figure and try to find out the pattern.
Have you noticed the below part in every partition?
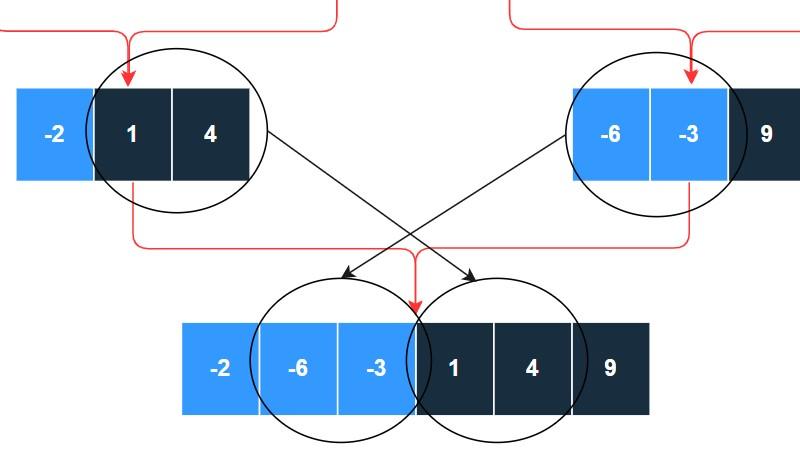
The end of the left part contains a consecutive number of positive elements, while the start of the right part contains a consecutive number of negative elements. And while merging, these two blocks just swap their positions.
Sounds interesting, right??
Now let’s not consider the two parts separately. Consider the whole subarray before merging. It looks like below,
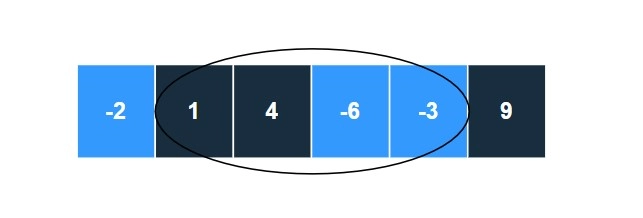
Our only interest is the encircled part.
Now the question is, how can we swap the blocks??
Simple just rotate the array(encircled part) left by the length of the left positive part.
The rotation steps are as follows,
We will simply use the Reversal Algorithm for Array Rotation here.
Below is the implementation,
Code in C++(Without using any Extra Space)
#include<bits/stdc++.h>
using namespace std;
// reverse
void reverse(int arr[] , int lo , int hi) {
while(lo < hi) {
int temp = arr[lo];
arr[lo] = arr[hi];
arr[hi] = temp;
lo++;
hi--;
}
}
// rotate
void rotate(int arr[] , int start , int end , int rotation_length) {
reverse(arr , start , start + rotation_length - 1);
reverse(arr , start + rotation_length , end);
reverse(arr , start , end);
}
void merge(int arr[] , int lo , int mid , int hi) {
// positive_start = start_index of the positive element in the left_half
int positive_start = lo;
// negative_end = end_index of the negative element in the second half
int negative_end = mid + 1;
// find out the positive_start in the left_half
while(positive_start <= mid && arr[positive_start] < 0) positive_start++;
// find out the negative_end in the right_half
while(negative_end <= hi && arr[negative_end] < 0) negative_end++;
negative_end--;
// length of the subarry to be rotated
int total_length = negative_end - positive_start + 1;
// rotation length = length of the positive part in the left_half
int rotation_length = mid - positive_start + 1;
// left rotate of the subarray[positive_start , negative_end] by rotation_length
rotate(arr, positive_start, negative_end, rotation_length);
}
void divide(int arr[] , int lo , int hi) {
if(lo < hi) {
int mid = lo + (hi - lo) / 2;
divide(arr , lo , mid);
divide(arr , mid + 1 , hi);
merge(arr , lo , mid , hi);
}
}
void Rearrange(int arr[], int n)
{
// calling the divide method
divide(arr , 0, n - 1);
}
int main() {
// given array
int arr[] = {1 , -2 , 4 , -6, -3, 9};
// calculate size of the array
int n = sizeof(arr) / sizeof(arr[0]);
// call the function
Rearrange(arr , n);
// print the result
cout << "Resulting array is: ";
for(int i = 0 ; i < n; i++) {
cout << arr[i] <<" ";
}
}

You can also try this code with Online C++ Compiler
Output
Resulting array is: -2 -6 -3 1 4 9
Complexity Analysis
Time Complexity: O(nlogn)
Space Complexity: O(logn) for additional recursive calls.
Where n = size of the array.
Frequently Asked Questions
What is the Merge sort algorithm?
The Merge sort algorithm is one of the most important and efficient sorting algorithms. It is used to sort unsorted lists or arrays. It is a comparison-based sorting algorithm which follows the divide and conquer strategy.
What is the main idea behind the Merge sort algorithm?
The Merge sort algorithm follows the divide and conquers strategy. It continuously divides the array into several sub-arrays until the sub-arrays contain a single element. Then merge those subarrays in a manner that results in a sorted list.
What is the time and space complexity of the Merge sort algorithm?
The time complexity of Merge sort: O(nlogn)
The space complexity of Merge sort: O(n)
What do you mean by “constant extra space” in a problem?
For any problem, the term “constant extra space” means that the space(memory) you have taken to solve the problem doesn’t depend on the input variable.
Conclusion
This article extensively discussed Rearrange Positive and Negative Numbers With Constant Extra Space using the merge sort technique.
We started with the basic introduction. We discussed,
- Problem Statement
-
Solution using Merge Sort Technique
We hope that this article has helped you enhance your knowledge regarding Rearrange Positive and Negative Numbers With Constant Extra Space using the Merge Sort technique.
If you want to learn more, check out our articles on Find the Minimum Element in a Rotated Sorted Array, Multiple Left Rotation in an Array in O(1) and Merge Sort. Please upvote this blog to help other ninjas grow.
Explore our practice platform Coding Ninjas Studio to practice top problems such as Rearrange Array Alternately, Sum Of Two Arrays, etc. attempt mock tests, read interview experiences, interview bundle, follow guided paths for placement preparations and much more.!
Happy Reading!