Table of contents

Introduction

Examples of Recursion

2.1.

Factorial of a number

2.2.

Fibonacci Series

Tail Recursion

3.1.

Code - Non-tail-recursive

3.2.

Code - Tail recursive

Strategy for solving Recursive Problem:

Benefits of using Recursion:

Drawbacks of using Recursion:

Frequently Asked Questions

7.1.

What is tail recursion, and what is it used for?

7.2.

Why do we need base cases?

7.3.

What are some of the recursion's drawbacks?

7.4.

What are the basic qualities of recursive functions?

Conclusion

Last Updated: Jun 26, 2024

Recursion in Python

Author Sanjana Yadav

Introduction

The process of describing something in terms of itself is known as recursion.

In the physical world, two parallel mirrors facing each other would be an example. Any item in the way would be mirrored recursively.

We know in Python that a function can call other functions. It's even feasible that the function will call itself. Recursive functions are the name given to these sorts of constructs.

The image below shows the syntax and working of recur, a recursive function.

Every recursive function must contain a base condition that terminates the recursion; otherwise, the function will call itself indefinitely.

The Python interpreter restricts recursion depths to avoid endless recursions, resulting in stack overflows.

The maximum depth of recursion is set to 1000 by default. If the limit is exceeded, RecursionError is thrown.

Examples of Recursion

Factorial of a number

The product of all positive numbers less than or equal to n, indicated by n! is the factorial of a non-negative integer n.

Code

def fact(n):
    if n == 1:
        # base case, when to discontinue recursion
        return 1
    else:
        return n*fact(n-1)
        # recursive call

print(fact(5))
# initial call

Output

Fibonacci Series

Fibonacci numbers, abbreviated as Fn, constitute a sequence known as the Fibonacci sequence, in which every number is the addition of the two preceding ones. The most common starting points are 0 and 1.

The Fibonacci series is 0,1,1,2,3,5,8….

Code

def fibo(n):
    if n<=1:
        return n
        # base case, when n is 1 or 0, return the number as it is
    else:
        return fibo(n-1)+fibo(n-2)
        # recursive case, when n > 1, return the sum of the previous two numbers

print(fibo(10))
# 10th fibonacci number is 55

Output

Also See, Intersection in Python

Must Read Recursion in Data Structure

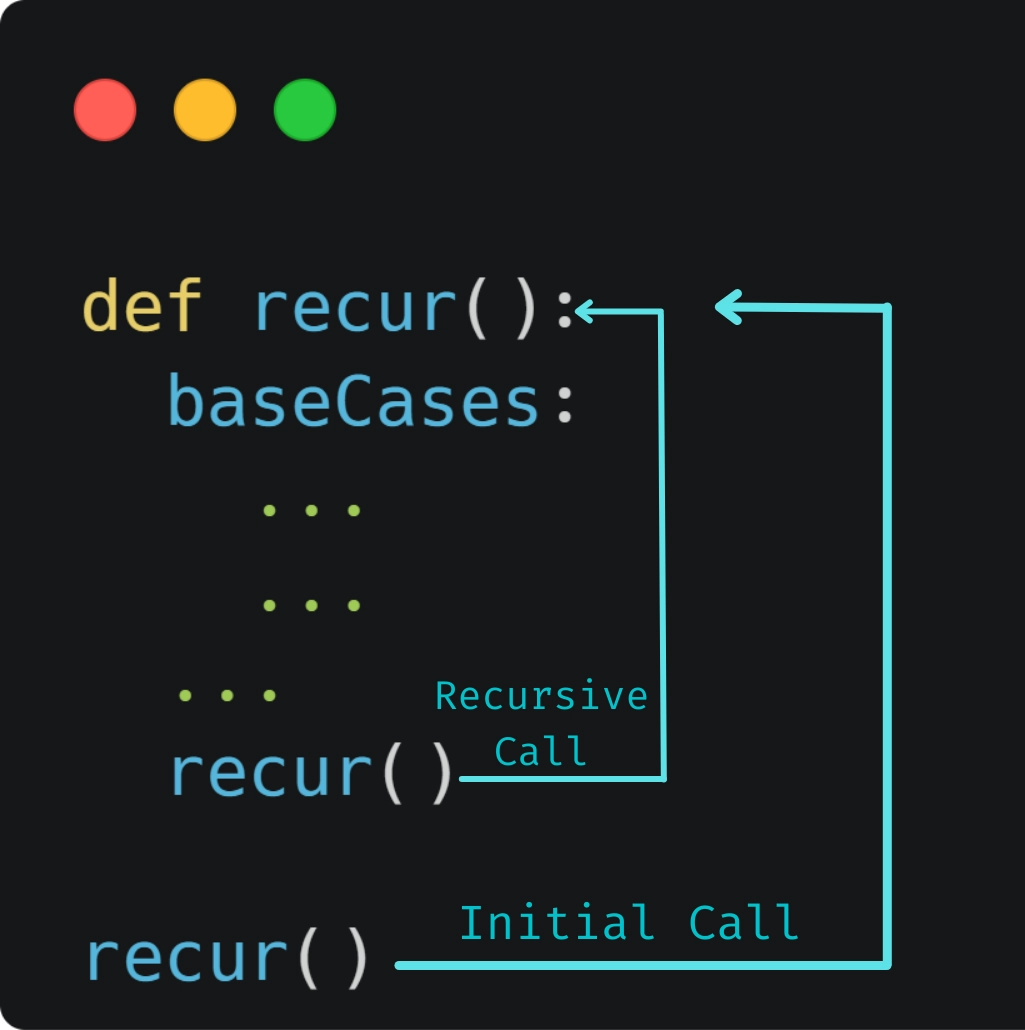
Tail Recursion

A special sort of Recursion in which a function's last procedure is a recursive call. Instead of establishing a new stack frame, the loop can be avoided by performing the request in the existing stack frame and returning the output. The compiler may optimize tail-recursion, making it better than non-tail recursive routines.

Most of the modern-day compilers convert tail call recursive calls into go-to statements on their own

Is it feasible to utilize a tail-recursive function instead of a non-tail recursive function to optimize a program?

Consider a recursive function to implement the sum of consecutive numbers up to n.

Code - Non-tail-recursive

def recurSum(x):
    if x == 0:
        return 0
        # base case, if x is 0, return 0
    else:
        return x + recurSum(x - 1)
        # recursive case, if x is not 0, return x + recurSum(x - 1)

print(recurSum(5))
# inital call

Compiler Interpretation

recurSum(5)
5 + recurSum(4)
5 + (4 + recurSum(3))
5 + (4 + (3 + recurSum(2)))
5 + (4 + (3 + (2 + recurSum(1))))
5 + (4 + (3 + (2 + (1 + recurSum(0)))))
5 + (4 + (3 + (2 + (1 + 0))))
5 + (4 + (3 + (2 + 1)))
5 + (4 + (3 + 3))
5 + (4 + 6)
5 + 10
15

Output

With that much function overhead, normal recursion is not optimized at all

Code - Tail recursive

def recurSum(x, runSum=0):
    if x == 0:
        return runSum
        # base case, if x is 0, return running sum
    else:
        return recurSum(x - 1, runSum+x)
        # recursive case, if x is not 0, return recurSum(x - 1, runSum+x)

print(recurSum(5))
# inital call

Compiler interpretation

recurSum(5, 0)
recurSum(4, 5)
recurSum(3, 9)
recurSum(2, 12)
recurSum(1, 14)
recurSum(0, 15)
15

Output

Since there is much less function overhead than usual recursive functions, that’s why it is considered optimized recursion.

Strategy for solving Recursive Problem:

The strategy for solving a recursive problem is that first, we have to think about the smallest size of problems and write down their solution that is nothing but abase case, now when we solved the base case then we go through the recursive case and at last we have to assemble all these smaller cases to solve the bigger cases so combining both of the base case and recursive cases we got the solution of our original problems which may have of any size.

Benefits of using Recursion:

By using recursion in our code we can make our program clean and elegant.
Hereby using recursion, we can solve the more and more complex programs by broken down into simpler subproblems and finding the solution of them through which collectively we solve whole the task.
In Recursion, It takes fewer lines of code to solve a problem.
One thing that is easier, by using recursion is that sequence generation other than using some nested iteration

Drawbacks of using Recursion:

Sometimes it is hard to follow the logic behind the recursion as not all the problems can be solved using recursion.
Here, If you don’t define the base cases then the code would run infinitely.
Recursive calls are inefficient as they take up a lot of memory spaces and time.
They are hard to debug as the function calling itself in a loop and it is hard to understand which call is causing the issue.

Frequently Asked Questions

What is tail recursion, and what is it used for?

If the recursive call is the last and only call in the recursive function, then it is considered as tail recursion, it is used to further optimize the recursive function and reduce the function overhead

Why do we need base cases?

Base cases are the most important part of any recursive function, without base cases, the function will execute infinitely and never end and will cause RecursionError in python.

What are some of the recursion's drawbacks?

In recursion, we’ve to be very careful writing base cases or there will be memory overflow or stack overflow if the base case isn’t written correctly, or the limit of recursion exceeds during the program and at last, it’s really hard to debug.

What are the basic qualities of recursive functions?

In recursive programming, a larger problem can be easily broken down into smaller segments and then can easily be solved and the code structure becomes really easy to understand.

Conclusion

Cheers if you reached here! In this blog, we saw and learned Recursion in Python
We have also seen different types of examples and how to decide the base cases in recursion.
Further, we saw how to optimize recursion using the tail recursion technique.

If you want to master questions on recursions and practice for Interviews, you can visit Top Recursion and Backtracking Interview Questions.

Also check out - Rod Cutting Problem, Fibonacci Series in Python

Recommended Readings: