Introduction
Nowadays, data is everything, so much research is going on in data analysis and data representation. Graphs are convenient and easy to understand Data Structures to represent data.
Graphs contain nodes that store data and edges connecting those nodes or vertices. Here we will learn about some of the different types of the graph like regular, complete, bipartite, etc., in detail and with examples.
So without wasting any further time, let's get on with our topic.
Types of Graphs
There are many types of graphs, but here we will discuss some of them: complete graph, regular graph, bipartite graph, and complete bipartite graph.
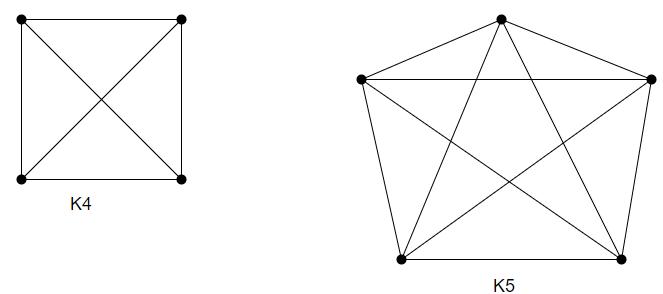
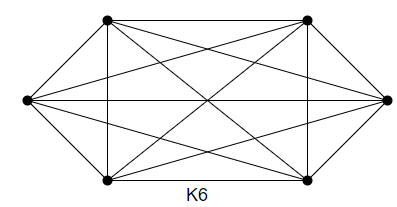
Complete Graph
Graph G, which has every vertex connected to every other vertex in the same graph G, is a complete graph. The complete graph is connected. The images below show the complete graphs starting from one vertex to six vertices.

Regular Graph
Graph G, in which all the vertices have the same degree K is known as a regular graph. A graph in which all the vertices have degree 2 is known as a 2- regular graph, and a complete graph, Kn is a regular graph of degree n-1.
Let’s discuss more regular graphs with the help of examples.
Example 1: Draw regular graphs for both degree 2 and degree 3.
Solution: The images below show the two regular graphs of degrees 2 and 3.
The left is degree 2, and the right image is a regular graph with degree 3.

Example 2: Draw a graph with five vertices and have degree 2.
Solution: The image below shows a regular graph with five vertices and degree 2.

Example 3: Draw a regular graph with five vertices and degree 3.
Solution: Drawing a regular graph with degree 3 of odd vertices is impossible. The number of vertices must be even as we have outlined for the six vertices below:

Bipartite Graph
A bipartite graph G=(V, E) has vertices V that may be partitioned into two subsets, V1 and V2, with each edge of G connecting a vertex of V1 to a vertex of V2. Kmn is the symbol for it, where m and n are the vertices in V1 and V2, respectively.
We will learn more about the bipartite graphs with the help of examples:
Example: Draw the bipartite graphs for k2,4 and k3,4. You can assume any number of edges.
Solution: Below is the representation of both parts of the above question.

Complete Bipartite Graph
Suppose the vertices V of a graph G = (V, E) can be partitioned into two subsets, V1 and V2, each vertex of V1 being linked to each vertex of V2. The graph is termed a full bipartite graph. Because each of the m vertices is connected to each of the n vertices, a complete bipartite graph has m.n edges.
We will learn more about the complete bipartite graphs with the help of examples:
Example: Draw the complete bipartite graph for K1,5 and K3,4.
Solution: The first image will show the complete bipartite graph of K1,5, and the second image shows K3,4.
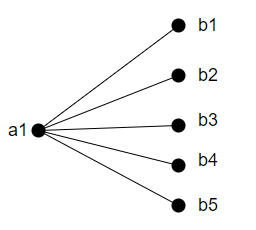
K1,5
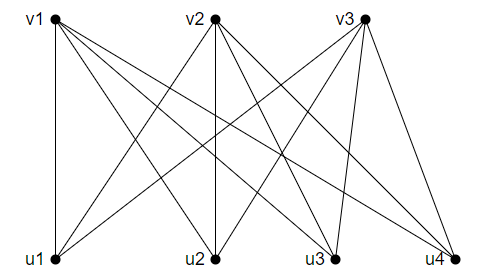
K 3,4