Relational Algebra

Selection or select operation ( σ )

The select operation, as the name suggests, is used to select the tuples from the relation which satisfies the given condition. It is denoted by sigma (σ).

Syntax: σ _(condition) (r), where σ is the selection operator, the condition is a given predicate, r is the relation.

Consider the following employees' relationship. The attributes are emp_id, emp_dept, emp_name and emp_salary.

Example 1: σ_{(emp_id=1)} (employees) will select the tuple with emp_id as 1. 

So the first row from the employees' table will be selected. It is important to note that the σ operator only selects the concerned tuple but does not project the result. To do that, we need to use the Π operator along with the σ operator.

We can use relational operators like >, <, =, >= etc along with the selection operator. We can also use logical operators like AND, OR, NOT.

Example 2: σ_{(emp_dept=”HR” AND emp_salary>12000)} (employees) 

The following query will select tuples with department name as "HR" and whose salary is greater than 12000. Clearly, first and third tuples will be selected.

Essential points about select operation:

1. It selects the tuples from the relation that satisfy the given predicate.
2. It follows commutative property.
3. We can use logical operators as well as relational operators with select operation.
   Also See, Multiple Granularity in DBMS

Rename operations (ρ)

It is a simple operation. Through rename operation, we can change the name of the table, name of the attributes of both. It is denoted by ρ.

Syntax: ρ _{new_name} (r);  where new_name is the name which is to be assigned to the relation or the attribute, r is the relation.

Example 1: Consider a relation R, with attributes (x, y, z). 

• ρ _R1 (R) will rename the relation R to R1.
• ρ _{R1 (a, b, c)} (R) will rename the relation R to R1 and also the attributes x, y, z to a, b, c respectively. We can also rename only some of the attributes.
• ρ  _{(a, b, c)} (R) will rename only the attributes of the relation R to a, b and c respectively without renaming R.

Essential points about the select operation:

1. Used to rename the attributes and the table.
2. We can rename one or more than one attribute, with or without renaming the relation.

Union operation (U)

Consider two tables T1 and T2. The union operation is used to get all the tuples that are present in table T1 or table T2 or in both. Before we move ahead, it is important to understand the union operation with an example.

Consider two tables (say T1 and T2) having attributes as (A, B) and (C, D), respectively.

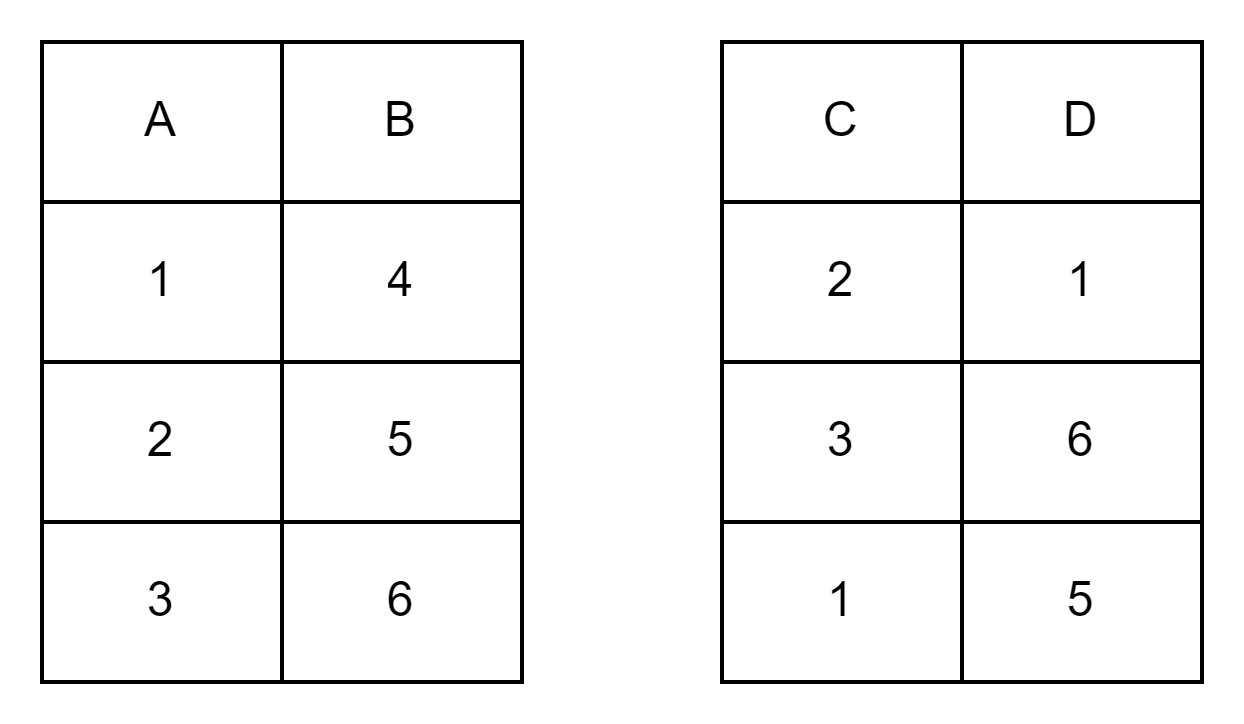
(T1 U T2) would result in the table below.

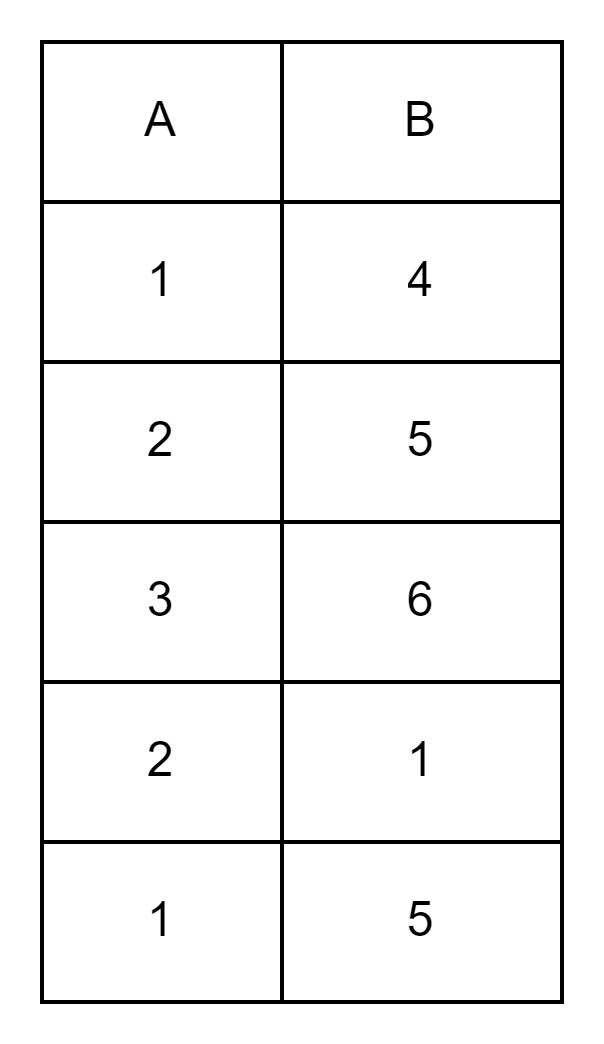
The third tuple of T1 and second tuple of T2 is the same, but the union operator does not allow duplicate tuples. It is one of the important properties of relational algebra.

The union operation can be performed only if:

1. Both the tables have the same number of attributes. Therefore the degree of both the tables should be the same.
2. The domain of the corresponding attribute in both the tables must be the same and compatible. Suppose the domain of attribute A in table T1 is "integer" while the domain of attribute B in table T2 is "varchar"(set of characters). If we try to perform the union operation on both the tables i.e. (T1 U T2), it would not be possible to do so. However, if both the attributes have "integer" or "varchar" as their domain, we can successfully perform union operation. The important point here is that the corresponding attribute should have the same domain.

Essential points about union operation:

1. It can be performed only if the number of attributes is the same in both the tables.
2. The domain of the corresponding attribute must be the same.
3. Union operation removes the duplicate tuples, if any.

Set difference operation(-)

Consider two relations X and Y. The set difference operation (X - Y) represents all the tuples that are present in relation X but not in relation Y. It is important to note that the rules that were applicable for union operation to be possible are also applicable to set difference operation. 

The degree of both the relation should be the same and also the corresponding attribute should be compatible.

Syntax: X - Y; where X and Y are two relations.

Example 1:  σ_(student) - σ_(monitor)  . The following query would select all the students from a table who are not monitored.

Cartesian product (X)

The cartesian product of two relations X and Y is obtained by merging each tuple of relation X with every tuple of relation Y. We can select tuples from a single table at a time. However, if we need to select tuples from multiple tables, we first need to find the cartesian product and then, based on some condition, we get selected tuples. The Cartesian product is the first step of any "join" operation. We will discuss joins later.

Consider the following two tables. Let the first table be A and the second table be B.

Therefore the cartesian product A X B can be represented as:

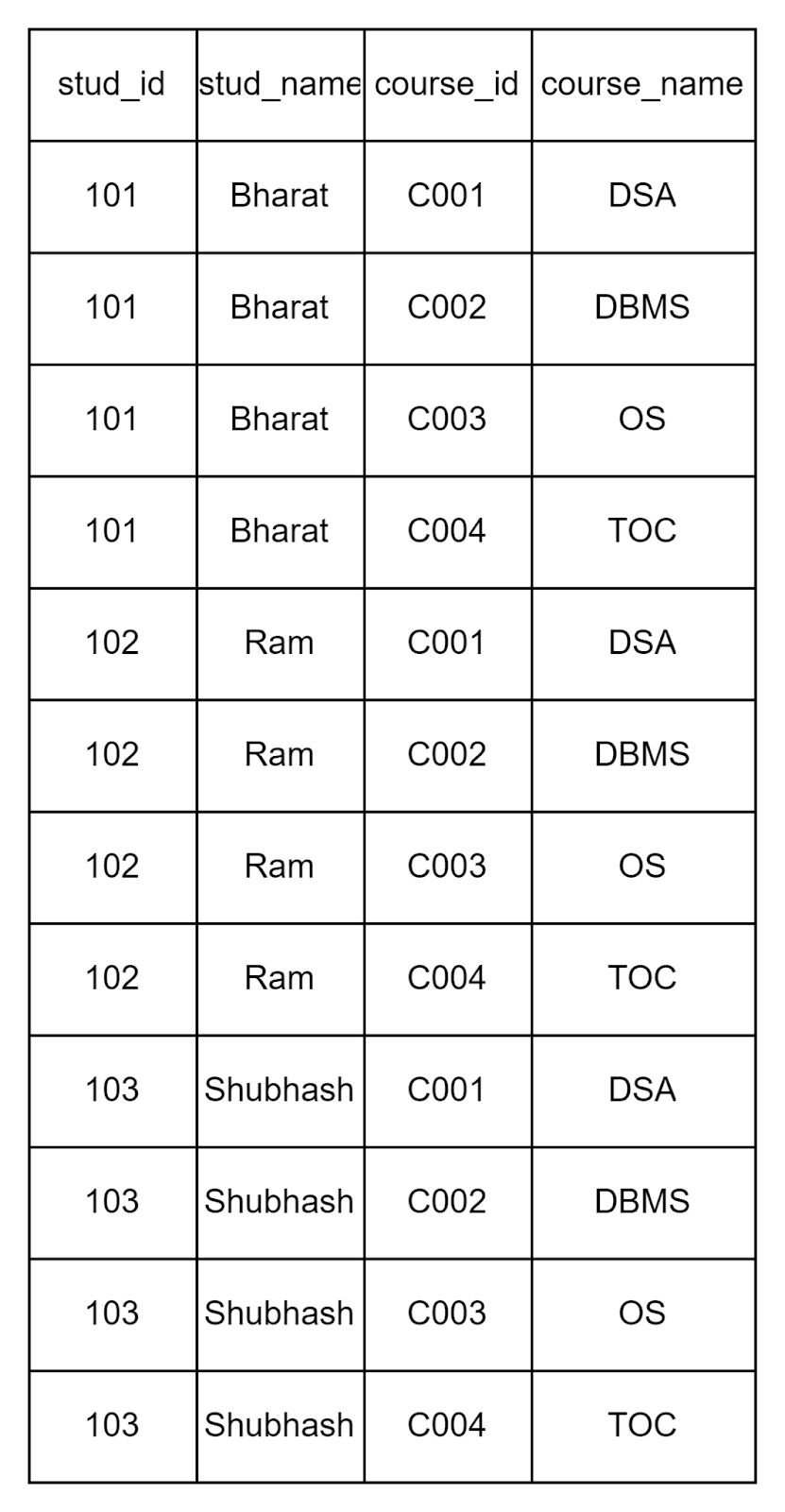
Here we can see that every tuple in the first table is repeated exactly four times, because the number of tuples in the second table is 4.

To find a cartesian product, we just have to merge each of the tuples from the first table with every tuple of the second table. If the number of tuples in table A is m and the number of tuples in table B is n, then we will have mn number of tuples in A X B.

Essential points about cartesian product:

1. It is used to merge columns from two tables. Tables need not be different.
2. It is the fundamental process in Join operations.
3. Both minimum and the maximum number of tuples in A X B will be mn, where m is the number of tuples in A and n is the number of tuples in B.

Till now, we have seen various operations of relational algebra. These are also known as fundamental operations. There are certain operations that can be derived using these fundamental operations. Join is one such operation.

You can also read about the Multiple Granularity Locking.

Join operations

Cartesian product is of no use if we are unable to retrieve any information from it. But if we put some conditions,based on that condition, we may get tuples from the cartesian product A X B .

Join is defined as a cartesian product followed by a selection operation.

(X, σ) -> ⨝

The general join operation is also called theta join. 

Consider the above table. Suppose we want only the tuples for students with the name Ram.

So we can write something like A ⨝_{(stud_id=102)} B. 

We will see various types of Joins now.

Natural Join (*)

When join operation is performed on two tables having a common attribute with the same name, it is known as natural join. Consider the following two tables. Let them be named as R and S.

R * S will be:

As we can see, only student id 101 and 102 are matching in both the tables. Hence the tuples corresponding to them are selected. It is important to note that the common attribute here also has the same name.

Outer Joins

There are three types of outer joins:

• Left outer join ( denoted by the symbol ⟕ )
• Right outer join( denoted by the symbol ⟖ )
• Full outer join ( denoted by the symbol ⟗ )

Left outer join ( ⟕ )

Consider the following two tables, A and B.

Here if we try to do A ⟕ B, we will get

Here all the tuples of A will be projected. If some value of a common attribute is missing in table B, we add the tuples from A but keep NULL in tuples from table B.

In the left join all the tuples of table A are present, but not necessarily all the tuples from B.

Right outer join (⟖)

Consider the following two tables, A and B.

The right join A ⟖ B will be represented by:

The right outer join is going to contain all the tuples from table B. Here since there is no student with stud_id=105 in table A, the value in the corresponding stud_name is NULL.

Full outer join (⟗)

The full outer join contains all tuples from both tables. The full outer join of the above table represented as A and B can be represented as:

Also Read, Apache Spark

Frequently asked questions

1. What is relational algebra?
   It is a procedural query language that uses various operations to obtain results from relations.
    
2. What are the basic operations of relational algebra?
   The basic operations of relational algebra include selection, projection, cartesian product, union, rename and set difference.
    
3. What is join in relational algebra?
   Join can be defined as a cartesian product followed by a selection operation.
    
4. Which query language is based on relational algebra?
   Structured Query Language(SQL).

Key Takeaways

• Relational algebra is a procedural query language.
• There are six basic operations in relational algebra viz. selection, projection, cartesian product, union, rename and set difference.
• Join operation can be described as a cartesian product followed by a selection operation.
• Various types of joins are natural join, theta join, equi join and outer join.

Also Read - Cardinality In DBMS

Aggregation in DBMS

Super Keys in DBMS

Never stop learning. Explore more here!

Also, you can check out the Top 100 SQL Problems to get hands-on experience with frequently asked interview questions and land your dream job.

Happy Learning.