Remove All Leaf Nodes from BST

Introduction

A BST (Binary Search Tree) is a tree in which all the nodes follow the properties shown below:

In comparison to its parent (root) node, the left sub-key tree has a lower value. The right sub-key tree's value is greater than or equal to the key value of its parent (root) node.

In this article, we will discuss the problem called "Remove All Leaf Nodes from BST." Let's discuss this without wasting your time!

Problem Statement

In this problem statement, we have a binary search tree, and we want to delete the leaf nodes.

Let's begin with an example to better understand the stated problem.

Sample Examples 

Example 1:

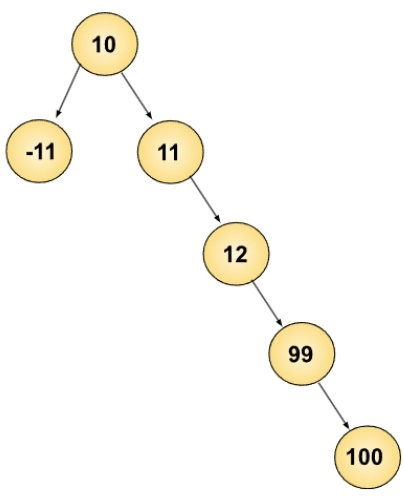
Input: 

10 11 -11 12 99 100 

Output

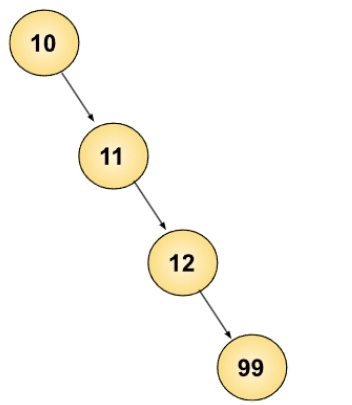
10 11 12 99 

Explanation

Initially, we have a given binary tree of 10 11 -11 12 99 100.  So, after making the diagram, we can easily see that the leaf nodes are -11 and 100. Therefore both the values are eliminated in the output.

Example 2:

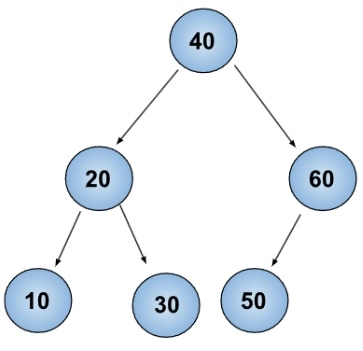
Input

40 20 10 30 60 50

Output

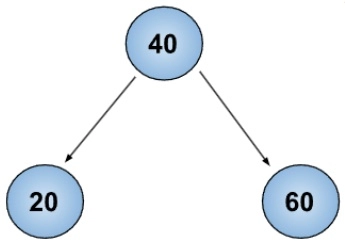
40 20 60

Explanation

We have given a binary tree 40 20 10 30 60 50. So, if you create the diagram, you can clearly identify the leaf nodes that are 10, 30, and 50 in this case. Hence we have removed these three from the output as per the problem statement.

Approach 

We can solve this problem by regular tree traversal algorithms. As we know, a node is a leaf node if it has neither a left nor a right child. The node becomes an internal node if it has either of the children. We can use any traversal, like preorder, inorder, and post orderer traversal. 

Let's now discuss the algorithm for this approach.

Algorithm 

1. Traverse the tree. If the root is NULL, return NULL.
    
2. Delete the node if it is a leaf node.
    
3. Recursively delete all leaf nodes in the left subtree.
    
4. And also, delete all leaf nodes from the right subtree recursively. Assign new left and right children if there is any modification in the subtree's root node.
    
5. To check if the nodes have been deleted or not, traverse the tree.

Implementation 

Let's see the code in C++ language.

#include <iostream>
using namespace std;



// Structure of a node
struct node
{
  int data;
  struct node *left, *right;
    node (int x)
    {
        data = x;
        left = right = NULL;
    }
};



// Helper function for traversing a tree.
void traverse (struct node *root)
{

  if (!root)
    return;

  std::cout << root->data << " ";

  traverse (root->left);

  traverse (root->right);


}


struct node *delete_leaf (struct node *root)
{

  if (!root)
        return root;
  if ((!root->left) && (!root->right))
    {
        free (root);
        return NULL;

    }

  root->left = delete_leaf (root->left);
  root->right = delete_leaf (root->right);
  return root;


}

int main ()
{

  	// Make binary tree for testing purpose
  	struct node *root = new node (20);

  	root->left = new node (21);
  	root->right = new node (22);
  	root->left->right = new node (-21);
  	root->right->left = new node (89);
  	root->right->left->right = new node (90);
  	std::cout << "Tree before deletion of the leaves:\n";
  	traverse (root);
  	std::cout << "\nTree after the deletion of leaves:\n";
  	delete_leaf (root);
  	traverse (root);
  	return 0;
}

Output:

Tree before deletion of the leaves:
20 21 -21 22 89 90 
Tree after the deletion of leaves:
20 21 22 89 

Now, let's check the code in Java language. We will first change it to Inorder, and then we will delete the leaf node.

public class Main
{
  static class Node
  {
    int data;
    Node left;
    Node right;
  }


// Creating a newNode in the binary search tree.
  static Node newNode (int data)
  {
    Node temp = new Node ();
    temp.data = data;
    temp.left = null;
    temp.right = null;
    return temp;
  }


// Inserting a Node in the binary search tree.
  static Node insert (Node root, int data)
  {
    if (root == null)
      return newNode (data);
    if (data < root.data)
      root.left = insert (root.left, data);
    else if (data > root.data)
      root.right = insert (root.right, data);
    return root;
  }


// Function for inorder traversal in a BST.
  static void inorder (Node root)
  {
    if (root != null)
    {
    	inorder (root.left);
    	System.out.print (root.data + " ");
    	inorder (root.right);
    }

  }


// Delete leaf nodes from the binary search tree.
  static Node leafDelete (Node root)
  {
    if (root == null)
        return null;
    if (root.left == null && root.right == null)
        return null;

	// Else recursively delete in left and right
	// subtrees.
    root.left = leafDelete (root.left);
    root.right = leafDelete (root.right);
    
    return root;
  }


// Driver code
  public static void main (String[]args)
  {
    	Node root = null;
    	root = insert (root, 30);
    	insert (root, 20);
    	insert (root, 15);
    	insert (root, 25);
    	insert (root, 40);
    	insert (root, 35);
    	insert (root, 45);
    	System.out.println ("Inorder before Deleting the leaf Node. ");
    	inorder (root);
    	System.out.println ();
    	leafDelete (root);
    	System.out.println ("Inorder after Deleting the leaf Node. ");
    	inorder (root);
  }
}

Output

Inorder before Deleting the leaf Node. 
15 20 25 30 35 40 45 
Inorder after Deleting the leaf Node. 
20 30 40 

Time Complexity 

The time complexity of the above code is O(N) (where N is the number of elements in the tree). We are traversing throughout the tree exactly one time which makes the complexity O(N).

Space Complexity 

The space complexity of the above code is O(N) (where N is the number of elements in the tree). The Space Complexity worst case occurs in the skew binary tree where the recursion goes N node deep until it hits.

Check out this problem - Connect Nodes At Same Level