Introduction
The problem states that we need to remove BST nodes having a value in the given range. After removing all the nodes in the range [min-max], the final output should also be the binary search tree. Let’s recap what is Binary search tree in brief, and what are the prerequisites to solve this question.
Binary Search Tree
A binary Search Tree is a particular type of binary tree in which keys in the left subtree are always smaller than the root node, and nodes in the right subtree are always greater than the root node. To know more about the Binary search tree, you can refer to this.
Prerequisites
To delete the nodes in the binary search tree. To know about this, you can refer to this link.
Sample Examples
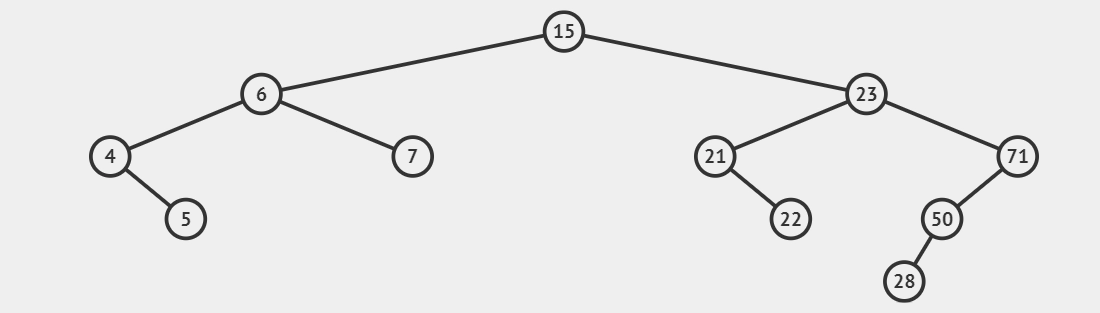
Input: Given the BST as shown below, and range is [4,7].
Output:

Explanation: The node values in the range [4,7] are 4,5,6 and 7 in the given binary search tree. Hence we have remove BST nodes having a value in the given range.
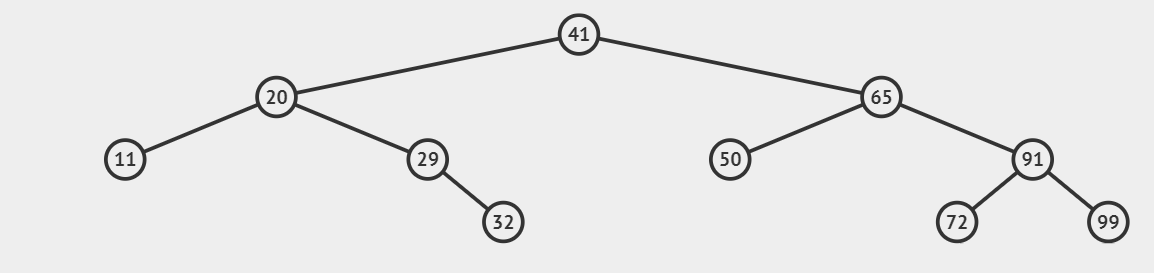
Input: Given the BST as shown below, and range is [90,100].
Output:
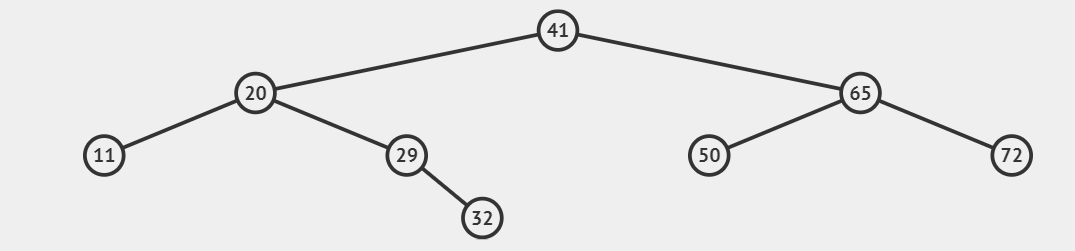
Explanation: The node values in the range [90,100] are 91 and 99 only in the given binary search tree. Hence we have remove BST nodes having a value in the given range.
Solution Approach
To remove BST nodes having a value in the given range[min, max], we can have two possible cases:
- Nodes are in the given range
- Nodes are not in the given range.
If nodes are not in the given range, we need not do anything. We will just move to the next node, but when nodes are in the given range, we need to delete the nodes in the binary search tree. The idea to solve this problem is simple; we will traverse the tree in preorder traversal, i.e., we will make sure that for any current node, its left and right subtrees are already processed. Now, whenever we find the node in the given range, we will simply call the delete function of BST.
Algorithm
- Traverse the tree in the preorder traversal by fixing the left and right subtrees of the node.
- Now check for the current node value is in the given range or not.
- If the value is not in the given range, do nothing.
- If the current node is in the given range, call for delete node function.
- Check for base condition. If the root value is NULL, return NULL.
Implementation in C++
// C++ implementation of the above approach
#include <bits/stdc++.h>
using namespace std;
// structure of the binary search tree node
class Node {
public:
int value;
Node * left, * right;
Node(int value) {
this -> value = value;
left = NULL;
right = NULL;
}
};
Node * leftMost(Node * root) {
if (!root)
return NULL;
while (root -> left)
root = root -> left;
return root;
}
// A Utility function to delete the nodes in the Binary search tree
Node * deleteNode(Node * root) {
// If nodes have only the single child or no child
if (!root -> left) {
Node * child = root -> right;
root = NULL;
return child;
} else if (!root -> right) {
Node * child = root -> left;
root = NULL;
return child;
}
Node * next = leftMost(root -> right);
// copying the content of inorder successor to this node
root -> value = next -> value;
// deleting the inorder successor
root -> right = deleteNode(root -> right);
return root;
}
// A utility function to remove BST nodes having a value in the given range
Node * BSTremoveRange(Node * root, int min, int max) {
// Base case
if (!root)
return NULL;
// traversing in the preorder fashion by fixing the left and right subtrees
root -> left = BSTremoveRange(root -> left, min, max);
root -> right = BSTremoveRange(root -> right, min, max);
// if given root value is in Range then call deleteNode function
if (root -> value >= min && root -> value <= max)
// delete the nodes in the binary search tree
return deleteNode(root);
// if root value is not in range
return root;
}
// A utility function to insert a new
// Node with given value in BST
Node * insert(Node * root, int value) {
Node * newnode = new Node(value);
// Pointer to start iterating the array
// from the root node
Node * curr = root;
// prev pointer will note the trailing of start pointer
Node * prev = NULL;
while (curr != NULL) {
prev = curr;
if (value < curr -> value)
curr = curr -> left;
else
curr = curr -> right;
}
// If the prev is NULL it means that the tree is empty
// The new node is the root node
if (prev == NULL)
prev = newnode;
// if the new value is lesser than the leaf node
// make the newNode as the left child of leaf node
else if (value < prev -> value)
prev -> left = newnode;
// otherwise make the newNode as right child of leaf node
else
prev -> right = newnode;
// Returns the prev pointer
// where we have inserted the newNode
return prev;
}
void Inorder(Node * root) {
// if the root node is NULL
if (!root)
return;
Inorder(root -> left);
// printing the root value
cout << root -> value << " ";
Inorder(root -> right);
return;
}
// Driver Program to test above functions
int main() {
Node * root = NULL;
root = insert(root, 41);
int nodesValues[] = { 20, 65, 11, 29, 50, 91, 32, 72, 99 };
for (int i = 0; i < 9; i++) {
insert(root, nodesValues[i]);
}
cout << "Inorder Traversal before Deletion : ";
Inorder(root);
root = BSTremoveRange(root, 20, 40);
cout << endl << "Inorder Traversal before Deletion: ";
Inorder(root);
cout << endl;
return 0;
}
Output:
Inorder Traversal before Deletion : 11 20 29 32 41 50 65 72 91 99
Inorder Traversal before Deletion: 11 41 50 65 72 91 99Complexity Analysis
Time Complexity: O(n*h)
Explanation: O(n*h) because in the worst case, every node can be in the range of [min - max], so for every node, you have to go and find its successor in O(h).
Space Complexity: O(1)
Explanation: We are just constants; it will not be considered extra Space. Hence space complexity is O(1) to remove BST nodes having a value in the given range.