Solution Approach
The solution to the problem is pretty straightforward. We will use an array to store the inorder traversal of the tree. Add a preceding and a trailing zero to set the inorder predecessor of the leftmost leaf and the inorder successor of the rightmost leaf as zero. Traverse again in an inorder fashion. For each node i, in the traversal, replace the node’s value with the sum of its inorder predecessor and successor stored in the array created earlier.
The algorithm of the solution is:
-
Take a binary tree you want to make the replacements on.
-
Display the preorder traversal of the given binary tree.
-
Create a temporary array that contains the inorder traversal of the given binary tree. This array will be used as a reference to get the inorder predecessor and successor of a node. Add a preceding and trailing zero in the temporary array.
-
Again traverse the given binary tree in an inorder manner and replace the value of node i with temp[i-1] + temp[i+1], where temp[i-1] is the inorder predecessor, and temp[i+1] is the inorder successor.
- Display the preorder traversal of the obtained binary tree.
Python Implementation
'''A class to create the binary tree'''
class Node:
'''Constructor of the class'''
def __init__(self, data):
self.data = data
self.left = self.right = None
'''Function to store the Inorder Traveral of given binary tree in temp array'''
def InorderTraveral(root, temp):
'''Base Case if tree is empty'''
if (not root):
return
'''Traversing for left tree recursively'''
InorderTraveral(root.left, temp)
'''Storing the value of root node in temp'''
temp.append(root.data)
'''Traversing for right tree recursively'''
InorderTraveral(root.right, temp)
'''Function that performs replacing nodes'''
def ReplacingNodes(root, temp, i):
'''Base Case if tree is empty'''
if (not root):
return
'''Traversing for left tree recursively'''
ReplacingNodes(root.left, temp, i)
'''Replacing the root node with the sum of its predecessor and successor'''
root.data = temp[i[0]-1] + temp[i[0]+1]
i[0] += 1
'''Traversing for right tree recursively'''
ReplacingNodes(root.right, temp, i)
'''Function that takes the root node and replaces node with the sum of its inorder predecessor and successor'''
def ReplaceNodeWithSum(root):
'''Base Case if tree is empty'''
if (not root):
return
'''creating a temp array that stores the inorder traversal of the binary tree'''
temp = []
'''Storing 0 at start for the inorder predecessor of the leftmost leaf'''
temp.append(0)
InorderTraveral(root, temp)
''''Storing 0 at last for the Inorder successor of the rightmost leaf'''
temp.append(0)
i = [1]
ReplacingNodes(root, temp, i)
'''To print the preorder of the tree before and after replacing the nodes with the sum'''
def DisplayPreorder(root):
'''Base Case if the tree is empty.''
if (not root):
return
print(root.data, end = " ")
'''Recursively traverse the left subtree'''
DisplayPreorder(root.left)
'''Recursively traverse the left subtree'''
DisplayPreorder(root.right)
''' Driver Function'''
def main():
''' Creating a binary tree'''
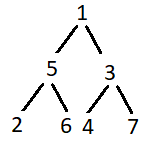
root = Node(1)
root.left = Node(5)
root.right = Node(3)
root.left.left = Node(2)
root.left.right = Node(6)
root.right.left = Node(4)
root.right.right = Node(7)
'''Display preorder traversal of the given tree'''
print("Preorder Traversal of Given Binary Tree:")
DisplayPreorder(root)
''' Calling the ReplaceNodeWithSum method on the given binary tree'''
ReplaceNodeWithSum(root)
'''Display preorder traversal after replacing the nodes with the sum'''
print("\nPreorder Traversal After Replacements:")
DisplayPreorder(root)
'''Executing Main'''
main()

You can also try this code with Online Python Compiler
Output
Preorder Traversal of Given Binary Tree:
1 5 2 6 3 4 7
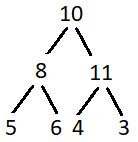
Preorder Traversal After Replacements:
10 8 5 6 11 4 3
Complexities
Time Complexity
The time complexity of the given solution is O(N), where N is the number of nodes in the given binary tree.
Reason: We are traversing the complete binary tree, which means we look at each node once. Hence, the complexity of O(N).
Auxiliary space complexity
The Auxiliary space complexity of the given solution is O(N), where N is the number of nodes in the given binary tree.
Reason: We are creating a temp array to store the inorder traversal of the given binary tree. The size of the temp array is N+2 (+2 for preceding and trailing 0). Hence, the complexity of O(N).
Frequently Asked Questions
What is a Binary Tree?
A binary tree is another type of tree data structure that contains a single root node and two disjoint subtrees called the left and the right subtree.
What is Inorder Traversal of a Tree?
Inorder Traversal is a Tree traversal algorithm where we follow the LNR rule that first traverses the left subtree, then looks at the root node, and moves on to traverse the right subtree.
What is an inorder predecessor in a given binary tree?
The inorder predecessor is the node that comes just before the given node in the inorder traversal. It is the rightmost leaf of the left subtree of the given node.
What is an inorder successor in a given binary tree?
The inorder successor is the node that comes just after the given node in the inorder traversal. It is the leftmost leaf of the right subtree of the given node.
What is Preorder traversal?
Preorder traversal is a tree traversal algorithm that works on the NLR principle. First, traverse the given node, then traverse the left subtree, followed by the traversal of the right subtree.
Conclusion
In this article, we discussed the problem of replacing each node in a binary tree with the sum of the node’s inorder predecessor and successor. We discussed the implementation and complexity of the solution to the problem.
I hope you would have gained a better understanding of these topics now!
Recommended problems -
Are you planning to ace the interviews of reputed product-based companies like Amazon, Google, Microsoft, and more?
Attempt our Online Mock Test Series on Coding Ninjas Studio now!

Happy Coding!