Replace every array element by multiplication of previous and next elements

Introduction

In this blog, we will try to grab hold of a single-dimensional ‘Array’ data structure problem. Through that problem, we will try to understand how to approach any array data structure problem. The examples presented will help you clear your concepts, Pseudocode will provide you with an immediate solution, and the implementation part will give you a detailed understanding of every step.

What is an Array data structure?

A collection of elements stored at contiguous memory locations is an Array. The elements stored in the array are of the same type. The contiguous memory locations of the array make it easier to calculate the position of each element in the array.

The first element is at index 0. As we transverse the array, the index increases by 1 till n-1 if there are n elements in the array. 

Array

Problem statement

Firstly, we will have a look at what exactly the problem says.

Given an array of ‘n’ elements. In that array, every element should be replaced by the product of its previous and next elements.

The two exceptions to this can be:

1. The first element will be replaced by the product of the first and the second elements.
2. The last element will be replaced by the product of the second last and the last elements.

Example 1

Explanation:

In the image below, we can observe how the output array gets its elements by the multiplication of the previous and the next elements. For now, we have excluded the first and the last elements of the output array which are exceptions for the above problem statement.

Example 2

Explanation:

In the image below, we can observe how the output array gets its elements by the multiplication of the previous and the next elements. This time, we have included the first and the last elements of the output array which are exceptions for the above problem statement.

Example 3

Explanation:

In the image below, we can observe how the output array gets its elements by the multiplication of the previous and the next elements. This time, we have put zero as the first element and have included the first and the last elements of the output array which are exceptions for the above problem statement.

Example 4

Explanation:

In the image below, we can observe how the output array gets its elements by the multiplication of the previous and the next elements. This time, we have put zero as the last element and have included the first and the last elements of the output array which are exceptions for the above problem statement.

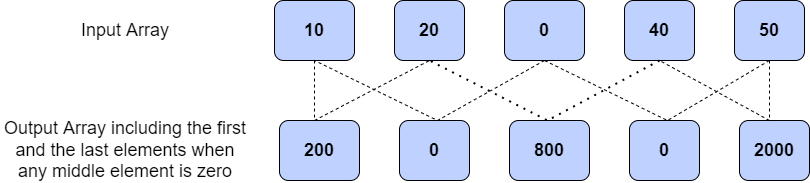
Example 5

Explanation:

In the image below, we can observe how the output array gets its elements by the multiplication of the previous and the next elements. This time, we have put zero as the middle element and have included the first and the last elements of the output array which are exceptions for the above problem statement.

Also see,  Rabin Karp Algorithm

Approach

Step-1:

Initially, we will create a temporary array of the same length as that of the input array. Here, we have considered an example array of 5 elements.

Temporary array, temp[] will be used to store the elements derived after the previous and the next elements of the input array is multiplied.

Step-2:

As the first element of the output array will be an exception, so in the output array, the first element will be the multiplication of the first and the second element of the input array.

Step-3:

The second element will be the multiplication of its previous and next elements. There are no exceptions here. Similarly, we will get the values for the next two elements of the output array. 

In case there are more elements than we have considered, the same procedure will be followed for them.

Step-4:

Now, for the last element, which is again an exception, that will be the multiplication of the last and the last second elements of the array.

Step-5:

The temporary array will be returned in the form of an output array.

Pseudo Code

static int[] mul(int nums[]){
        int[] temp = new int[nums.length];
        temp[0] = nums[1];
        temp[nums.length-1] = nums[nums.length-2];
        for(int i=1; i<nums.length-1; i++ )
        {
            temp[i] = nums[i-1] * nums[i+1];
        }
        return temp;
    }

You can also try this code with Online Java Compiler

Run Code

Implementation in Java

//Java Program code of the problem of replacing every element of array by multiplication of previous and next elements.
import java.io.*;
import java.util.*;
import java.lang.Math;
public class Main
{
    static int[] mul(int nums[]){
        int[] temp = new int[nums.length];
        temp[0] = nums[1] * nums[0];
        temp[nums.length-1] = nums[nums.length-2] * nums[nums.length-1];
        for(int i=1; i<nums.length-1; i++ )
        {
            temp[i] = nums[i-1] * nums[i+1];
        }
        return temp;
    }
public static void main(String[] args) {
  int[] arr = {1,2,3,4,5};
  int [] temp = new int[arr.length];
  temp=mul(arr);
  for(int i=0; i < temp.length;i++){
      System.out.print(temp[i] + " ");
  }
}
}

You can also try this code with Online Java Compiler

Run Code

Output

arr[]={2, 3, 8, 15, 20}

Complexity Analysis

• Since we have just one loop running in the solution provided. The time complexity for the code mentioned above will be O(n).
• We have not used any extra space to store any value. Hence, the space complexity for the code mentioned above will be O(1).

Check out this problem - First And Last Occurrences Of X