Approach
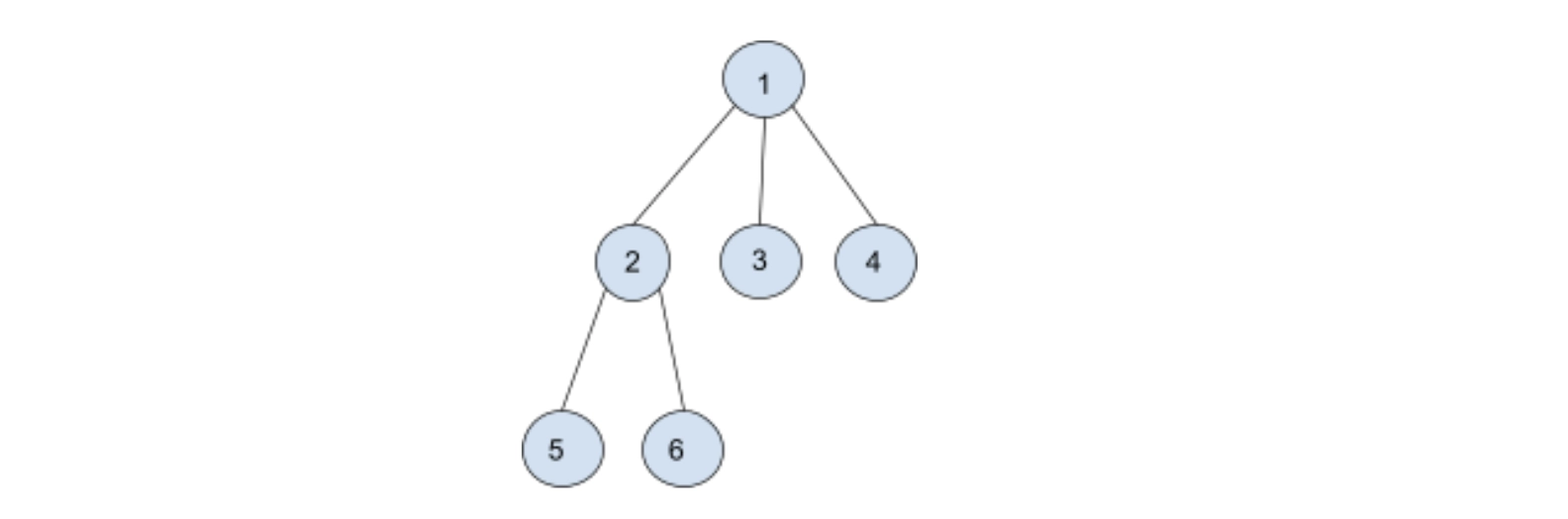
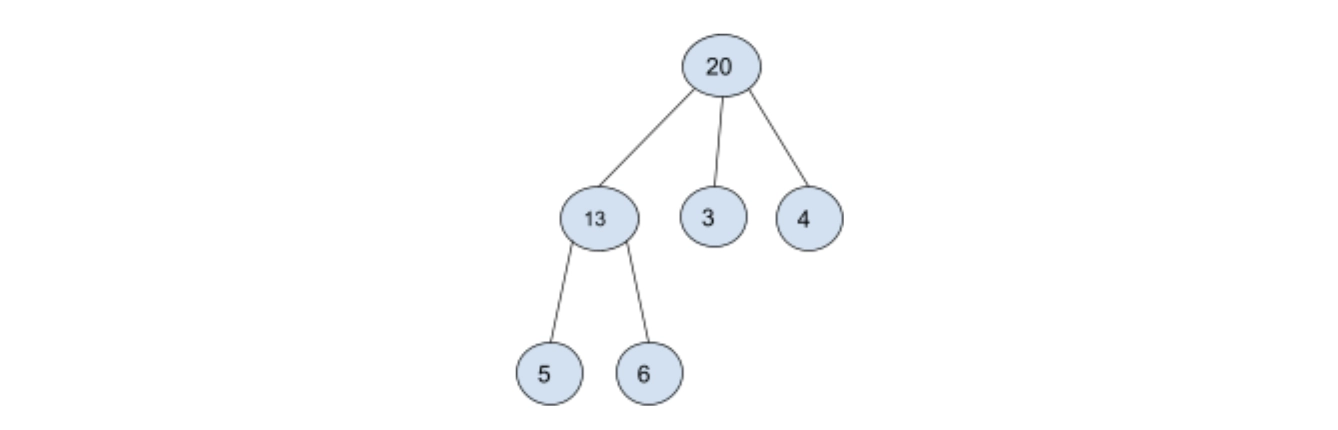
In the current node, we need to store the sum of each node in its subtree. Since leaf nodes do not have any children, so it will always be an excellent choice to start from the leaf nodes and then move to their parents. In this way, we can recursively reach the root.
Therefore, having the root of the tree, we can first replace the children with its subtree sum, and after that, we can simply add on all the values stored in the children nodes with the value of the current node to get the sum of its subtree. Thus, we can replace the whole tree with the sum of its subtree nodes.
The solution can be understood with the below algorithm.
Algorithm
-
The function replaceSubtreeSum(Node* root) will take the current node as input and return the sum of its subtree.
-
First, we will check if the ‘root’ is a NULL pointer. If yes, the subtree sum will be zero.
-
We will iterate through the children of the ‘root’ and call replaceSubtreeSum(), with the current child as the ‘root,’ so that its value gets replaced with its subtree sum.
-
Now we will take the sum of all the child values along with the ‘root’ value and finally replace it with the current ‘root’ value.
Below is the program with this algorithm.
Program
// C++ program to replace values with the sum of subtree.
#include <iostream>
using namespace std;
// Structure for the node of the N-ary tree.
typedef struct Node
{
// Value of the node.
int value;
// Number of children of the current node.
int numChild;
// Array containing pointers to children.
Node** children;
// Default constructor.
Node()
{
value = 0;
numChild = 0;
}
// Constructor.
Node(int len, int data)
{
value = data;
children = new Node*();
numChild = len;
}
} Node;
// Function to replace the value of N-ary tree with the subtree sum.
int replaceSubtreeSum(Node* root)
{
// Checking if the root is null.
if (!root)
return 0;
// Iterating through the array of children.
for (int i = 0; i < root->numChild; i++)
{
// Storing the subtree sum of children.
root->value += replaceSubtreeSum(root->children[i]);
}
// Returning the sum of nodes in the root's subtree.
return root->value;
}
// Function for preorder traversal of the N-ary tree.
void preorder(Node* root)
{
if (!root)
return;
cout << root->value << " ";
for (int i = 0; i < root->numChild; i++)
preorder(root->children[i]);
}
// Main Function.
int main()
{
/* Generating the following N-ary Tree.
1
/ | \
6 8 5
/ | \
2 7 3
Root of the Tree.*/
Node *root = new Node(3, 1);
root->children[0] = new Node(3, 6);
root->children[1] = new Node(3, 8);
root->children[2] = new Node(3, 5);
root->children[0]->children[0] = new Node(3, 2);
root->children[0]->children[1] = new Node(3, 7);
root->children[0]->children[2] = new Node(3, 3);
// Printing preorder traversal before replacements.
cout << "Preorder Traversal before replacements: ";
preorder(root);
// Calling the function for replacements.
replaceSubtreeSum(root);
// Printing preorder traversal after replacements.
cout << endl << "Preorder Traversal after replacements: ";
preorder(root);
return 0;
}

You can also try this code with Online C++ Compiler
Output
Preorder Traversal before replacements: 1 6 2 7 3 8 5
Preorder Traversal after replacements: 32 18 2 7 3 8 5
Time Complexity
O(N), where ‘N’ is the number of total nodes in the N-ary tree.
Explanation: As we recursively go through each node only once, there are in total n calls being made, so O(N).
Space complexity
O(N), where ‘N’ is the number of tota nodes in the N-ary tree.
Explanation: ‘N’ number of nodes used to store the data of the N-ary tree constitutes a total space of O(N).
Frequently Asked Questions
What are some real-world applications of the Binary Tree data structure?
One of the most common data structures is the binary tree. It also serves as a foundation for a variety of additional user-defined data structures. This data structure and its implementation are used in a variety of real-world applications, either directly or indirectly. Many compression algorithms, such as Huffman coding, are implemented using binary trees. In networking, binary trees are also employed. Internally, binary trees are also used by decision trees. Binary trees are used to implement priority queues in heap data structures.
What is the Red-Black tree data structure?
The Red-Black Tree is a unique self-balancing tree that possesses the following characteristics: each Node is either red or black in color, the root is always black in color, there can't be a red parent or red child for a red node, the number of black nodes on each path from the root node to a NULL node is the same.
How can you determine whether a binary tree is a subtree of another binary tree?
You've been given two binary trees and must determine whether one of them is a subtree of the other. A binary tree subtree A node from BT and all of its descendants make up BT, which is a tree T. T1 is a subtree of binary tree BT in the following example.
How can you determine whether a binary tree is a subtree of another binary tree?
Let's say we have a binary tree called T. We'll now see if a binary tree S is a subtree of T. To begin, look to see if there is a node in T that is also in S. Once you've located this common node, see if the nodes below are also part of S. If this is the case, we can reasonably conclude that S is a subtree of T.
In a binary tree, how do you calculate the distance between two nodes?
Consider two binary tree nodes, n1, and n2, respectively. The least number of edges that must be crossed to get from one node to the other is equal to the distance between n1 and n2. It's crucial to remember that you travel the shortest path between the nodes.
Conclusion
The above blog has covered an important interview question frequently asked in big MNCs where Data Structures and Algorithms play an important role. Replacing every Node of an N-ary Tree with the sum of all its subtrees is a good question related to trees, which enhances your understanding of the traversal of trees from root to leaves. It also helps us to learn the way to obtain the sum of the subtree of the current Node.
Also check out - Inorder Predecessor
Find more such interesting questions on our practice platform Coding Ninjas Studio if you want to learn more before jumping into practicing, head over to our library section for many such interesting blogs. Keep learning.
Happy Coding!