Introduction
Given any two non-empty sets A and B, A relation R from A to B is a subset of the Cartesian product A x B and is derived by describing a relationship between the first element (say x) and the other element (say y) of the ordered pairs in A & B. Elements corresponding to x are called the domain of the given ordered pairs. In contrast, elements corresponding to y are called the range of the given ordered pairs.
5 Representations of Relations
Ordered Pair
In this set of ordered pairs of x and y are used to represent relation. In this, corresponding values of x and y are represented using parenthesis.
Example:
S: {(1,2), (2,4), (3,6)} Set of Ordered Pairs
Relation as a Matrix
In this, zero-one is used to represent the relationship between two sets. In this, if an element is present, then it is represented by 1; else, it is represented by 0. This method makes it easy to judge if a relation is reflexive, symmetric, or transitive just by looking at the matrix.
Suppose R is a relation from X={x1, x2, .....xn} to Y={y1, y2....yn}
It is represented by :-
M[i, j]={1, if (Xi, Yj) belongs to R
0, if (Xi, Yj) does not belong to R}
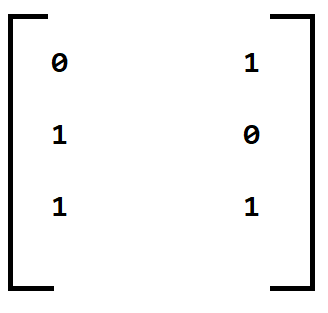
If A={1, 2, 3} and B={1, 2} and Relation R is
R = {(1, 2) (2, 1), (3, 1), (3, 2)}
then all corresponding value of Relation will be represented by “1” else “0”.
It is represented as:
Mapping Diagram
A mapping or an arrow diagram is a visual representation of a relation.
If S and T are finite sets and R is a relation from S to T. Let's see how a Relation R can be depicted using a mapping diagram.
Draw two ellipses for the sets S, and T. Write down the elements of S and elements of T column-wise in ellipses. Then draw a directed arrow from the first ellipse to the second ellipse if s is related to t and s ∈ S and t ∈ T.
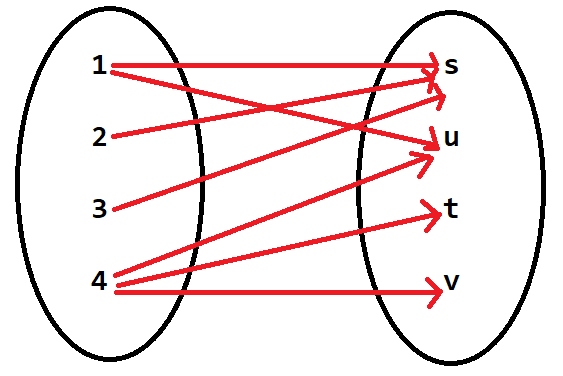
Let S = {1, 2, 3, 4}
T = {s, t, u, v}
R = {(1, s), (2, s), (3, s), (1, t), (4, t), (4, u), (4, v)}
Digraph
A relation can be represented using a directed graph(Digraph).
The number of vertices in the graph represents the number of elements in the set from which the relation has been defined. For each ordered pair, say (x, y) in the relation R, there will be a directed edge/arrow from the vertex 'x' to vertex 'y'.
Also, if there is an ordered pair (x, x), there will be a self-loop on vertex 'x.'
Example:
A = {1, 2, 3, 4}
R = {(1, 2) (1,3) (2, 4) (3, 4) (4, 1) (4, 4)}

Relation as a Table
A relation can be represented using a table. Relation R can be represented in a tabular form. It presents the elements of domain and range in a tabular way.
Make the table that contains rows equivalent to an element of S and columns equivalent to the element of T. Then place a cross (X) in the boxes, which represent relations of elements on set S to set T.
Let S = {1, 2, 3, 4}
T = {s,t,u,v}
R = {(1, s), (1, t), (2, u), (3, u), (4, v)}.






