Introduction
Have you ever come across a problem that requires you to rotate an array in the right or left direction, and you messed up? Then you are at the right place.
After reading this article, you will be confident to solve this and related problems flawlessly!!
In this article, we are going to learn a very interesting Reversal Algorithm for right rotation of an array. We will analyse this algorithm on the basis of its time complexity and space complexity and finally see its implementation.
Must Read, Array Implementation of Queue and Rabin Karp Algorithm
Problem Statement
You are given an array A of size n and a number k. Right-Rotate the array k times.
Array rotation means shifting the elements of the array by the specified positions in the specified direction, which can be either left or right.
Let’s see the sample input and output to understand clearly:
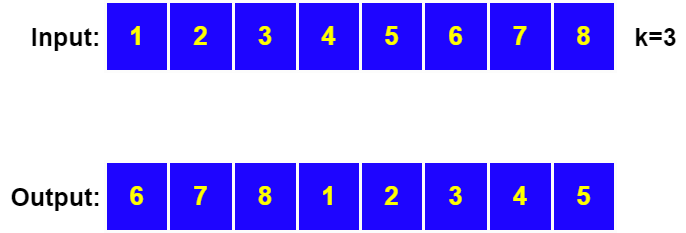
Note: The value of k can be less than or greater than n. When k>n, we will do k=k%n. Because rotating the array by n or a multiple of n will have no effect on the array.
The brute force approach can be, shifting all the array elements one by one towards the right. So, if we have to shift by ‘k’ places, we will be required to do the shifting k times. We know that to shift all the elements by one place towards the right is an O(n) operation. Hence, the total time complexity for shifting k elements will be O(n.k).
Can we improve our algorithm to get a better time complexity?
The answer is Yes, and that’s where we will introduce the reversal algorithm for right rotation of the array.
The following steps are to be followed in the reversal algorithm for right rotation of array:
- Reverse the whole array i.e. i=0 to i=n-1
- Reverse the subarray from i=0 to i=k-1
- Reverse the subarray from i=k to i=n-1
As you can see, mainly, we are using the function of reversing the array from index=start to index=end.
So, let’s see the pseudocode for array reversal:
|
while(start<end) { swap(arr[start],arr[end]); start++; end--; } |





