Introduction
Here in this blog, we are asked to see various approaches to reverse a path in a binary search tree using a queue. We already are familiar with the concept of the trees and binary search tree and also with the queue data structures. So, let's dig a little deeper into this blog.
Problem statement
In this problem, we are provided a binary search tree and we are asked to reverse its path around a node. Let us understand the problem statement with the help of an example. We need to keep in mind that for the binary search tree, the left node is smaller than the root node and the right node is larger than the root node. I.e left node<root node<right node.

Source: binary search tree
Sample example
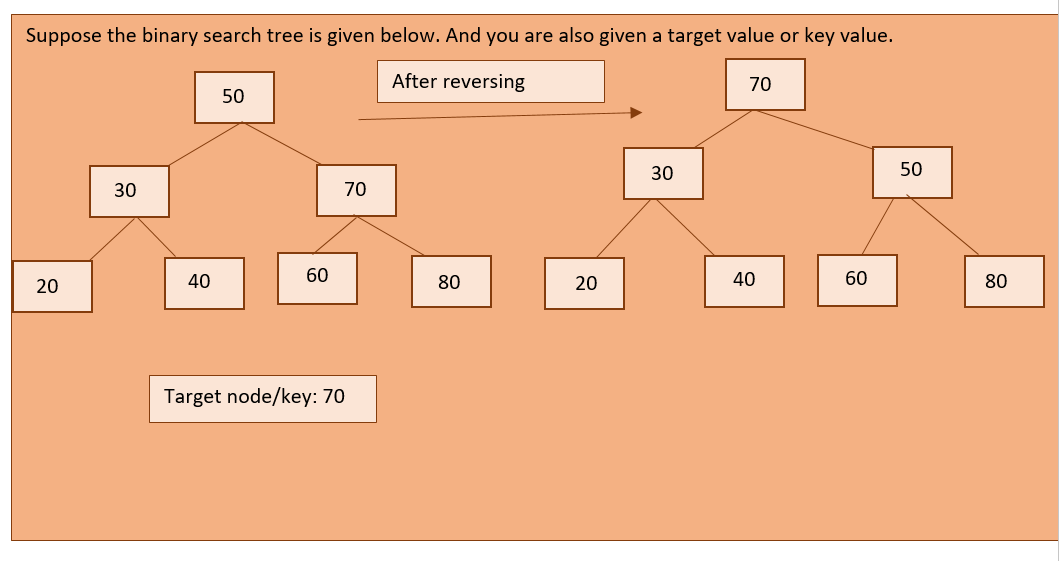
In the above diagram, we can clearly understand that we are given a binary search tree and a target node. And we have to reverse the path from the root node to the given target node. In the diagram given the inorder before reversing: 20 30 40 50 60 70 80
And inorder after reversing : 20 30 40 80 60 70 50
Recursive Approach
This approach is very simple to implement and straightforward. Because reversing a path from the root to the target node is similar to reversing all the node elements present on the path from the root to the target node. For example, if the path contains 1->2->3->4 from the root node to that target node. Then after reversing the path will become 4->3->2->1. In this recursive approach, we will enqueue/push all the values of nodes in the path from the root to the given target node and then replace the existing current node with the element at the front of the queue.

Source: recursive function
Let us see its algorithm.
Steps of Algorithm
Step 1: If the root is null, return null.
Step 2: if the root value is equal to the target, push the root into the queue and replace the root value with the queue’s front. Dequeue the element in front of the queue
Step 3: If the root value is less than the target, push it to the queue, call reversePathBST recursively for the root left child, and replace the root value with the element at the front of the queue. And remove the element at the top of the
Step 4: And if the value is greater push the root's value to the queue, call reversePathBST recursively for the root's right child, and then replace the root's value with the element at the front of the queue. And remove the element at the top of the queue.
Let us see the implementation of this approach in the next section of this blog.
Implementation in C++
#include <bits/stdc++.h>
using namespace std;
struct node
{
int key;
struct node * left, * right;
};
struct node * newNode(int item)
{
struct node * temp = new node;
temp -> key = item;
temp -> left = temp -> right = NULL;
return temp;
}
void inorder_tree(struct node * root)
{
if (root != NULL)
{
inorder_tree(root -> left);
cout << root -> key << " ";
inorder_tree(root -> right);
}
}
void Reverse_tree(struct node ** node, int & key, queue < int > & q1)
{
if (node == NULL) //If the tree is empty then
return;
if (( * node) -> key == key)
{ // if we find the key
q1.push(( * node) -> key); // we push it into our queue
( * node) -> key = q1.front(); // we change the first queue element with current
q1.pop(); // we pop the first element
}
else if (key < ( * node) -> key)
{ // if key is less than current node's value
q1.push(( * node) -> key);
Reverse_tree( & ( * node) -> left, key, q1); //recursive call
( * node) -> key = q1.front();
q1.pop();
}
else if (key > ( * node) -> key)
{ // if key greater than node key then
q1.push(( * node) -> key);
Reverse_tree( & ( * node) -> right, key, q1); //recursice call
( * node) -> key = q1.front();
q1.pop();
}
return;
}
struct node * insert_treenode(struct node * node, // function to insert node nodes in our BST
int key)
{
if (node == NULL)
return newNode(key); // if tree is empty we return a new node
if (key < node -> key) // else we push that in our tree
node -> left = insert_treenode(node -> left, key);
else if (key > node -> key)
node -> right = insert_treenode(node -> right, key);
return node; // returning the node
}
int main()
{
struct node * root = NULL;
queue < int > q1;
int target = 70;
root = insert_treenode(root, 50); //creating binary search tree
insert_treenode(root, 30);
insert_treenode(root, 20);
insert_treenode(root, 40);
insert_treenode(root, 70);
insert_treenode(root, 60);
insert_treenode(root, 80);
cout << "Inorder traversal before reversing: " << endl;
inorder_tree(root); //inorder of original tree
cout << endl;
Reverse_tree( & root, target, q1);
cout << "Inorder traversal after reversing: " << endl;
inorder_tree(root); //inorder of reversed tree
return 0;
}
Output:
Inorder traversal before reversing:
20 30 40 50 60 70 80
Inorder traversal after reversing:
20 30 40 70 60 50 80 Implementation in Java
import java.util.*;
public class reverse_Tree
{
static class node
{
int key;
node left, right;
};
static node root = null;
static Queue < Integer > q1;
static int target;
static node newNode(int item)
{
node temp = new node();
temp.key = item;
temp.left = temp.right = null;
return temp;
}
// for inorder traversal of BST
static void inorder_tree(node root)
{
if (root != null)
{
inorder_tree(root.left);
System.out.print(root.key + " ");
inorder_tree(root.right);
}
}
// reverse tree path using queue
static void reversePath_queue(node node)
{
if (node == null) //If the tree is empty,
return;
if ((node).key == target) // If the node key equal to target
{
q1.add((node).key);
(node).key = q1.peek();
q1.remove();
return;
}
// if key smaller than node key then
else if (target < (node).key)
{
q1.add((node).key);
// recursive call itself
reversePath_queue((node).left);
(node).key = q1.peek();
q1.remove();
}
// if key greater than node key then
else if (target > (node).key)
{
q1.add((node).key);
// recursive call itself
reversePath_queue((node).right);
(node).key = q1.peek();
q1.remove();
}
return;
}
static node insert_Node(node node, int key)
{
//If the tree is empty
if (node == null)
return newNode(key);
if (key < node.key)
node.left = insert_Node(node.left, key);
else if (key > node.key)
node.right = insert_Node(node.right, key);
return node;
}
public static void main(String[] args)
{
q1 = new LinkedList < > ();
target = 70;
root = insert_Node(root, 50);
root = insert_Node(root, 30);
root = insert_Node(root, 20);
root = insert_Node(root, 40);
root = insert_Node(root, 70);
root = insert_Node(root, 60);
root = insert_Node(root, 80);
System.out.print("Inorder traversal before reversing: "+ "\n");
inorder_tree(root); //inorder traversal of the BST
System.out.print("\n");
// reverse path till target
reversePath_queue(root);
System.out.print("Inorder traversal after reversing: "
+
"\n");
inorder_tree(root); //inorder traversal of the reversed BST
}
}
Output:
Inorder traversal before reversing:
20 30 40 50 60 70 80
Inorder traversal after reversing:
20 30 40 70 60 50 80
Let us analyze the time and complexity of this approach.
Complexity analysis
Time complexity
This approach will take O(log n) where n is the size of the array. Because in this approach, we are making comparisons and are using recursive calls to solve the problem again and again.

Space complexity
And it will take O(log n). Since we are not using any extra space to store it.
Must Read C Program to Reverse a Number





