Introduction
We have been given a binary tree, we need to reverse the alternate level nodes of the binary tree, as shown in the below example.
Example
Input
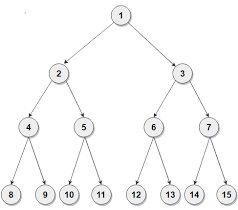
Output



We have been given a binary tree, we need to reverse the alternate level nodes of the binary tree, as shown in the below example.


If the current node is on an even level, this approach merely swaps the values of the children node because that switches elements on an odd level.
Consider the following scenario:
As a result, we refer to the recursive function for child elements as the same recursive function because this is a perfect binary tree. The stack of recursion might have been O(n) for a conventional binary tree.
/* C++ program to reverse alternate levels of a perfect binary tree */
#include <bits/stdc++.h>
using namespace std;
struct Node
{
int key;
Node *left, *right;
};
void preorder(struct Node *root1, struct Node* root2, int lvl)
{
/* checking for null roots */
if (root1 == NULL || root2==NULL)
return;
/* If the level is even, swap the subtrees. */
if (lvl%2 == 0)
swap(root1->key, root2->key);
/* Recursion for subtrees on the left and right. */
preorder(root1->left, root2->right, lvl+1);
preorder(root1->right, root2->left, lvl+1);
}
/* For root's left and right children, this function calls preorder(). */
void reverseAlternate(struct Node *root)
{
preorder(root->left, root->right, 0);
}
/* print inorder traversal */
void printInorder(struct Node *root)
{
if (root == NULL)
return;
printInorder(root->left);
cout << root->key << " ";
printInorder(root->right);
}
/* function to create a new node */
Node *newNode(int key)
{
Node *temp = new Node;
temp->left = temp->right = NULL;
temp->key = key;
return temp;
}
/* Main program */
int main()
{
struct Node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(6);
root->right->right = newNode(7);
root->left->left->left = newNode(8);
root->left->left->right = newNode(9);
root->left->right->left = newNode(10);
root->left->right->right = newNode(11);
root->right->left->left = newNode(12);
root->right->left->right = newNode(13);
root->right->right->left = newNode(14);
root->right->right->right = newNode(15);
reverseAlternate(root);
printInorder(root);
return 0;
}/* Java program to reverse alternate levels of a perfect binary tree */
class Main
{
static class Node
{
int key;
Node left, right;
};
static void preorder(Node root1, Node root2, int lvl)
{
/* checking for null roots */
if (root1 == null || root2 == null)
return;
/* If the level is even, swap the subtrees. */
if (lvl % 2 == 0) {
int t = root1.key;
root1.key = root2.key;
root2.key = t;
}
/* Recursion for subtrees on the left and right. */
preorder(root1.left, root2.right, lvl + 1);
preorder(root1.right, root2.left, lvl + 1);
}
/* For root's left and right children, this function calls preorder(). */
static void reverseAlternate(Node root)
{
preorder(root.left, root.right, 0);
}
/* print inorder traversal */
static void printInorder(Node root)
{
if (root == null)
return;
printInorder(root.left);
System.out.print(root.key + " ");
printInorder(root.right);
}
/* function to create a new node */
static Node newNode(int key)
{
Node temp = new Node();
temp.left = temp.right = null;
temp.key = (char)key;
return temp;
}
/* Main program */
public static void main(String args[])
{
Node root = newNode(1);
root.left = newNode(2);
root.right = newNode(3);
root.left.left = newNode(4);
root.left.right = newNode(5);
root.right.left = newNode(6);
root.right.right = newNode(7);
root.left.left.left = newNode(8);
root.left.left.right = newNode(9);
root.left.right.left = newNode(10);
root.left.right.right = newNode(11);
root.right.left.left = newNode(12);
root.right.left.right = newNode(13);
root.right.right.left = newNode(14);
root.right.right.right = newNode(15);
reverseAlternate(root);
printInorder(root);
}
}
15 4 14 3 13 5 12 1 11 6 10 2 9 7 8O(n),
Reason: Using recursion so that the time complexity will be O(n).
O(log n),
Reason: We are storing values in the variable so that the space complexity will be O(log n).
Must Read Recursion in Data Structure
It is a non-linear data structure of the tree type with a maximum of two offspring per parent. The root node is the node at the very top of a tree's hierarchy. The parent nodes are the nodes that include additional sub-nodes.
Following are the different types of binary trees: full binary tree, perfect binary tree, skewed binary tree, complete binary tree, and degenerate binary tree.
Binary trees are mostly used in computing for searching and sorting since they allow data to be stored hierarchically. Insertion, deletion, and traversal are some of the most frequent operations performed on binary trees.
We can use the postOrder traversal's recursive definition to travel to the left subtree, the right subtree, and the root.
We can use the preOrder traversal's recursive definition to visit the root, recursively travel to the left subtree, and then proceed to the right subtree.
In this article, we have reverse alternate levels of a perfect binary tree. We hope that this blog will help you understand the concept of a binary tree, and if you want to learn more about the binary tree, check out our other blogs on the binary tree, an introduction to binary tree, and binary search tree.
Recommended problems -
Refer to our guided paths on Coding Ninjas Studio to learn about Data Structure and Algorithms, Competitive Programming, JavaScript, etc. Enroll in our courses and refer to our mock test available. Have a look at the interview experiences and interview bundle for placement preparations.
Happy Coding!






