Rotate a Matrix by 180-degree

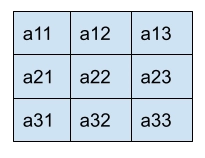
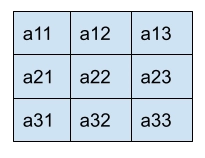
Swapping position approach

In the swapping position approach, we are swapping the position of the element in the first row with the elements of the last row in reverse order. Now the elements of the second row with a reverse of the second last row of the matrix and so on. For the middle row, that row itself will be printed in reverse order.

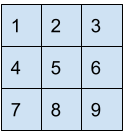
Matrix = 

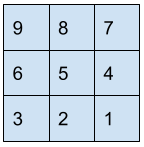
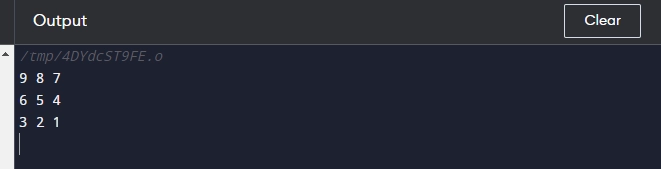
Swapping and reversing the first row with the last row.

Matrix = 

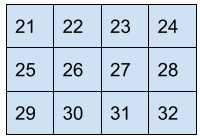
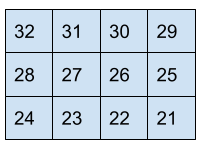
For the middle row, that row itself will be printed in reverse order.

Matrix =

Algorithm

1. There are two tasks to complete in order to rotate the given matrix. The first step is to find the swap elements of the matrix, and the second step is to rotate the matrix without using any extra space.
2. Now swap the elements at positions (i,j) with (j, i). 
3. Now run two loops, the outer loop from 0 to row count and the inner loop from 0 to the outer loop's index.
4. To rotate the matrix, if r is odd, then the middle row of the matrix is reversed. 
5. Now swap the value of matrix array[j][i] with [rows - j - 1][cols - i - 1] for the half of the size of rows.  
6. Now print the output.

Implementation in C++

#include <iostream>
#include<bits/stdc++.h>
#include <vector>
#include <algorithm>
#define pb push_back
#define vll vector<long long int>
using namespace std;
typedef long long int ll;

// Function to swap elements of the matrix
void do_swaps(int& a, int& b, int& c, int& d) 
	{
	  swap(a, b);
	  swap(c, d);
	}

//Function to rotate the matrix
void rotate(vector<vector<int>>& v) 
	{
    	size_t m = v.size();
    	size_t n = v[0].size();
    	for (size_t i = 0; i < m / 2; ++i)
    		{
        		for (size_t j = 0; j < n; ++j)
            	swap(v[i][j], v[m - i - 1][n - j - 1]);
    		}
    	if (m&1)
    	for (size_t i = 0; i< n/2; ++i)
        swap(v[m/2][i], v[m/2][n-i-1]);
}

//Function to print the output
void print(const vector<vector<int>>& v) 
{
	  size_t m = v.size();
	  size_t n = v[0].size();
	  for(size_t i = 0; i < m; ++i) 
	  {
    		for(size_t j = 0; j < n; ++j) 
    		{
      			cout << v[i][j] << ' ';
    		}
    		cout << '\n';
  		}
}

// Main function of the program
int main() 
{
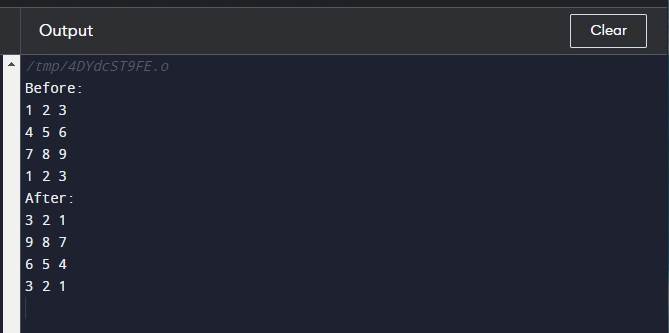
	  vector<vector<int>> m{{1,2,3}, {4,5,6}, {7,8,9}, {1, 2, 3}};
	  cout << "Before: \n";
	  print(m);
	  rotate(m);
	  cout << "\nAfter: \n";
	  print(m);
}

You can also try this code with Online C++ Compiler

Run Code

Output:

Time complexity

The time complexity of this approach is O(R*C). As we are rotating and swapping the matrix in the same loop, here, the time complexity of rotating is O(R), and that of swapping is O(C).

Space complexity 

The space complexity of this approach is O(1), as we are using constant extra space.

Frequently Asked Questions

What is the disadvantage of using printing the reverse order element approach?

When we rotate a matrix by printing the array in reverse order, we are traversing the whole matrix and printing the matrix again in the reverse order in the same loop. That means two nested loops have time complexities of O(N) each, resulting in the time complexity of the whole as O(N*N), but the space complexity of the program is O(n), i.e., the program is not ‘in place’, it is taking some extra space.

Why is the time complexity of the swapping approach in this program O(R*C)?

As we are rotating and swapping the matrix in the same loop, here, the time complexity of rotating is O(R), and that of swapping is O(C).

Why is the space complexity of the swapping approach in this program O(1)?

Because the algorithm is an in-place algorithm, the space complexity is O(1).

Conclusion

This article extensively discussed the problem of rotating a matrix by 180 degrees without using extra space.

We hope this blog has helped you enhance your knowledge regarding multi-dimensional array problems. After reading about the rotation of matrix, are you not feeling excited to read/explore more articles on this topic? Don't worry; Coding Ninjas has you covered. To learn, see time complexity, and Complexity Analysis.

Check out this problem - Matrix Median

Refer to our Guided Path on Coding Ninjas Studio to upskill yourself in Data Structures and Algorithms, Competitive Programming, JavaScript, System Design, and many more! If you want to test your competency in coding, you may check out the mock test series and participate in the contests hosted on Coding Ninjas Studio! But suppose you have just started your learning process and are looking for questions asked by tech giants like Amazon, Microsoft, Uber, etc. In that case, you must look at the problems, interview experiences, and interview bundle for placement preparations.

Nevertheless, you may consider our paid courses to give your career an edge over others!

Do upvote our blogs if you find them helpful and engaging!

Happy Learning!