Test Case
Below is an example of the test case.
Input
{
{1,2,3,4},
{5,6,7,8},
{9,10,11,12}
}
2
Output
{
{3,4,1,2},
{7,8,5,6},
{11,12,9,10}
}
Explanation
Given input Matrix is,
{
{1,2,3,4},
{5,6,7,8},
{9,10,11,12}
}
and k = 2.
After two rotations to the right of the matrix, the output comes out to be,
{
{3,4,1,2},
{7,8,5,6},
{11,12,9,10}
}
Below is the explanation,
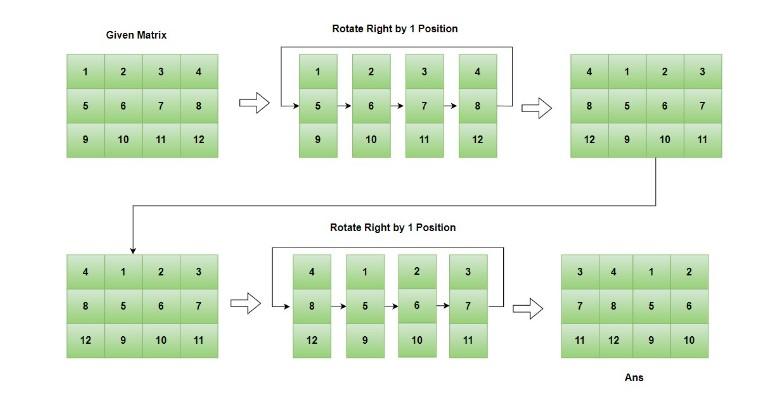
Solution
A simple solution to this problem is simply rotating each row to the right by k elements. If we do so, we will get our final answer.
If you want to learn about the right rotation of an array in detail, follow these articles on Array Rotation.
Below is the algorithm.
Algorithm
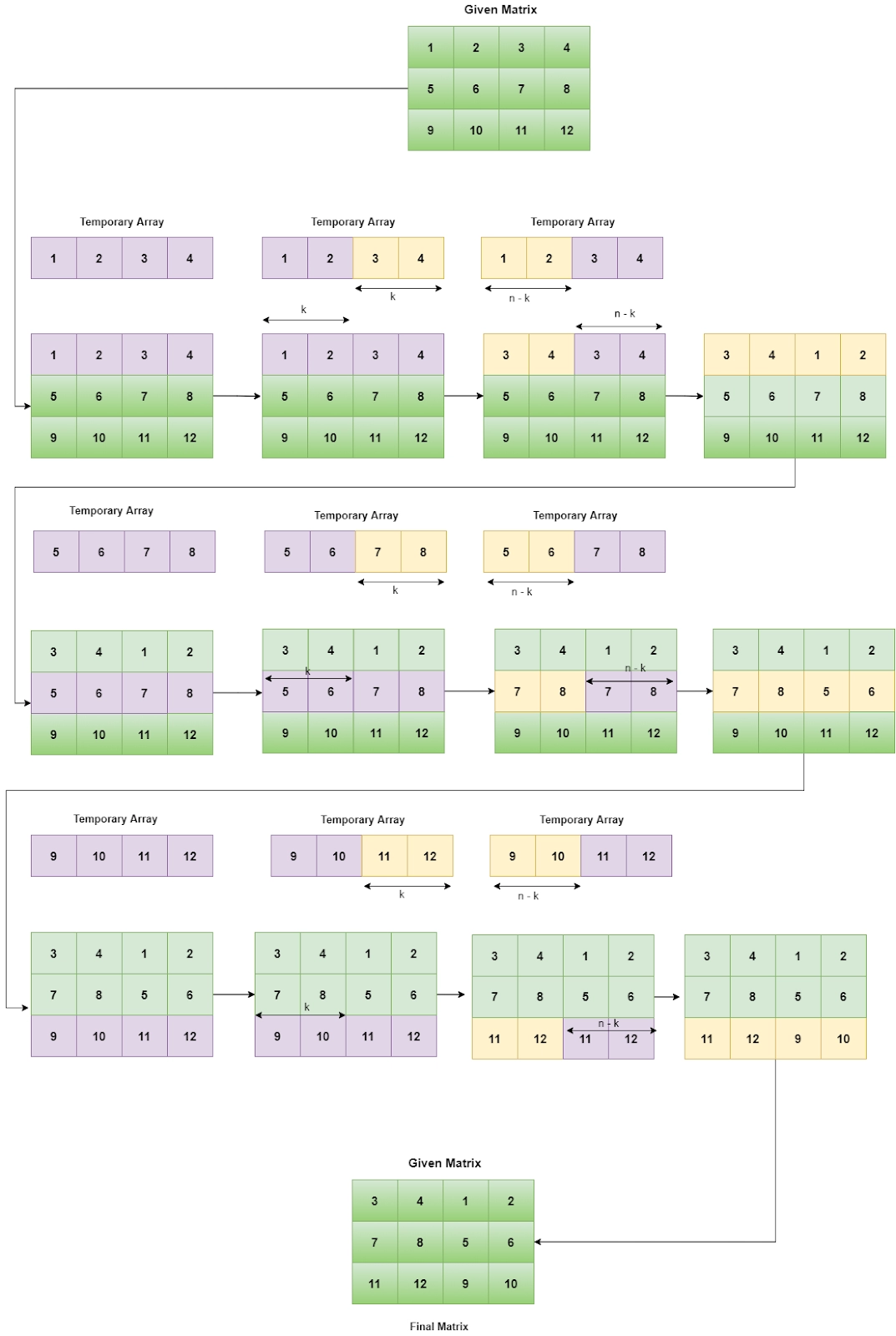
- Traverse each row of the matrix.
- Create a temporary array of sizes n (where n = number of columns)
- Copy the elements of the current row to the temporary array.
- Replace the current row's first k elements with the temporary array's last k elements.
- Replace the current row's last n - k elements with the temporary array's first n - k elements.
- Repeat the above process for all rows in the matrix.
Visualisation
Below is the visualisation of the above algorithm,
Implementation
Here, in this section, we will implement the above algorithm in different languages.
C++ Code
#include <bits/stdc++.h>
using namespace std;
#define m 3
#define n 4
int main()
{
int matrix[m][n] = {{1, 2, 3, 4}, {5, 6, 7, 8}, {9, 10, 11, 12}};
int k = 2;
// for the case when k > n
// here k = 2;
k %= n;
// traverse each row of the matrix
for (int i = 0; i < m; i++)
{
// for each row
int arr[n];
// copy all elements of the current row to the arr
for (int j = 0; j < n; j++)
{
arr[j] = matrix[i][j];
}
// replace the first k elements of the current row with the last k elements of the arr
for (int j = 0; j < k; j++)
{
matrix[i][j] = arr[n - k + j];
}
// replace last n - k elements of the current row with the first n - k elements of the arr
for (int j = k; j < n; j++)
{
matrix[i][j] = arr[j - k];
}
}
// print the matrix after rotation
for (int i = 0; i < m; i++)
{
for (int j = 0; j < n; j++)
{
cout << matrix[i][j] << " ";
}
cout << "\n";
}
return 0;
}

You can also try this code with Online C++ Compiler
Java Code
class Main {
public static void main(String[] args) {
int m = 3;
int n = 4;
// given k
int k = 2;
// given matrix
int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 } };
// for the case when k > n
// here k = 2;
k %= n;
// traverse each row of the matrix
for (int i = 0; i < m; i++) {
// for each row
int[] arr = new int[n];
// copy all elements of the current row to the arr
for (int j = 0; j < n; j++) {
arr[j] = matrix[i][j];
}
// replace the first k elements of the current row with the last k elements of the arr
for (int j = 0; j < k; j++) {
matrix[i][j] = arr[n - k + j];
}
// replace last n - k elements of the current row with the first n - k elements of the arr
for (int j = k; j < n; j++) {
matrix[i][j] = arr[j - k];
}
}
// print the matrix after rotation
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}
}

You can also try this code with Online Java Compiler
Python Code
# dimension of the matrix
m = 3
n = 4
# given k
k = 2
# given matrix
matrix = [[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]]
# for the case when k > n
# here k = 2;
k %= n
# traverse each row of the matrix
for i in range(0 , m):
# for each row
arr = []
# copy all elements of the current row to arr
for j in range(0 , n):
arr.append(matrix[i][j])
# replace the first k elements of the current row with the last k elements of the arr
for j in range(0 , k):
matrix[i][j] = arr[n - k + j]
# replace the last n - k elements of the current row with the first n - k elements of the arr
for j in range(k , n):
matrix[i][j] = arr[j - k]
# print the matrix after rotation
for i in range(0 , m):
for j in range(0 , n):
print(matrix[i][j] , end =" ")
print()

You can also try this code with Online Python Compiler
Output
3 4 1 2
7 8 5 6
11 12 9 10
Complexity Analysis
If you want to learn about time and space complexity, follow the Time and Space Complexity article.
Time complexity: O(MN)
Space Complexity: O(N)
Also see, Rabin Karp Algorithm
Frequently Asked Questions
What is the time and space complexity of traversing a matrix of size MxN?
Time Complexity: O(MN)
Space Complexity: O(1)
How many ways can we traverse a matrix?
There are mainly two ways we can traverse a matrix,
- Row Major Traversal
-
Column Major Traversal
What do you mean by row-major and column-major traversal for a matrix?
Row-major traversal: If we traverse a matrix row by row, it is called row-major traversal.
Column-major traversal: When we traverse a matrix column by column, it is called column-major traversal.
How to check if the given two matrices are equal?
To check whether two given matrices are equal or not, you can do the followings:
- Check if they have the same dimensions.
- Check if all corresponding pairs of elements in the two matrices are equal.
Conclusion
In this article, we have extensively discussed Rotate a Matrix Right by K Elements.
We started with the basic introduction, then we discussed,
- The Problem Statement
- A Test Case
- and Solution
We hope you have got some insight through this article regarding Rotating a Matrix Right by k Elements.
If you want to learn more, follow our articles on Operation On Matrices, Book Allocation Problem, How to Multiply Two Matrices, and Minimum Sum Path in a Matrix.
Explore our practice platform Coding Ninjas Studio to practice top problems, attempt mock tests, read interview experiences, interview bundle, follow guided paths for placement preparations and much more.!
Happy Reading!








