Row with the Maximum Number of 1’s

Approach 1: Brute force 

A straightforward method is to traverse each row one by one and count the number of 1’s in all the rows. Find the maximum of these and finally return the index of the row having the maximum number of 1’s.

Code in C++

#include <bits/stdc++.h>
using namespace std;

int row_with_max_1s(vector<vector<int>>matrix)
{
    int max_one = 0;          // maximum number of 1's

    int max_one_index = 0;    // index of the row having the maximum number of 1's

    for (int i = 0; i < matrix.size(); i++)
    {
        int count = 0;   // number of 1's in current row

        for (int j = 0; j < matrix[0].size(); j++)
        {
            if (matrix[i][j] == 1)
                count++;
        }
        if (count > max_one)
        {   max_one = count;
            max_one_index = i;
        }
    }

    return max_one_index;
}

int main()
{
    vector<vector<int>> matrix = {
        {0, 0, 1, 1, 1},
        {0, 0, 0, 0, 1},
        {0, 0, 0, 0, 0},
        {0, 1, 1, 1, 1},
    };
    int max_one_index = row_with_max_1s(matrix);

    cout << max_one_index;

    return 0;
}

 

Output

3

Complexity Analysis

Time Complexity: O(m*n) where m is the number of rows and n is the number of columns as we are using two nested loops of size m and n.

Space complexity: It is O(1) as we require constant extra space.

Approach 2: Binary Search 

As we already know that each row in the given matrix is in sorted order, an efficient approach for finding the maximum number of 1’s would be to use the binary search algorithm. 

The main idea is that we have to find only the first occurrence of 1 in every row as it is sorted, so every element after the first occurrence of 1 will be 1.

For this, we will use the lower_bound() function, which returns an iterator pointing to the first index of the element. 

Example:   

 

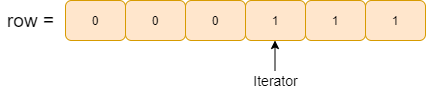
lower_bound(row.begin(),row.end(),1): it returns an iterator pointing to the first occurrence of 1. If 1 is not present it returns an iterator pointing to row.end() which is the element beyond the last element.

So, The total number of 1’s in a row = Iterator pointing beyond the last index of the current row - Iterator pointing to the first index of the 1.

Now, check for all the rows if the current row has the maximum number of 1’s, update maximum 1’s, and index having maximum 1’s seen so far.

Code in C++

#include <bits/stdc++.h>
using namespace std;

int row_with_max_1s(vector<vector<int>> matrix)
{
    int max_one = 0;    // maximum number of 1's
    int max_one_index = 0;    // index of the row having the maximum number of 1's

    for (int i = 0; i < matrix.size(); i++)
    {
        int ones = matrix[i].end() - lower_bound(matrix[i].begin(), matrix[i].end(), 1);

        if (ones > max_one)
        {
            max_one = ones;
            max_one_index = i;
        }
    }

    return max_one_index;
}


int main()
{
    vector<vector<int>> matrix = { {0, 0, 0, 0},
        {0, 0, 0, 1},
        {0, 0, 1, 1},
        {0, 0, 0, 1}
    };
    int max_one_index = row_with_max_1s(matrix);

    cout << max_one_index;
    return 0;
}

 

Output

2

Complexity Analysis

Time Complexity: O(m*logn) where m is the number of rows and n is the number of columns as we are traversing each row and using lower bound, which takes logn time.

Space complexity: It is O(1) as we require constant extra space.

Must Read Lower Bound in C++ You can also read about - Strong number in c

Approach 3: Efficient

In this approach, we take advantage of sorted rows.

Steps:

• We start from the last index of the first row of the matrix and move towards the left until we find a 0 and store its index.
   
• Now, we move downwards until we find a row having a 1 on that index. In this case, all the previous rows have fewer numbers of 1’s than this row because of the sorted property of rows.
   
• Again we move towards the left in this row until we find a 0, and we update the max_one_index to this row.
   
• We continue the above process until we reach the last row of the matrix.
   
• Finally, we return the index of the row having the maximum number of 1’s.
   

Let’s understand the above approach with an example:

 

max_one_index=0

 

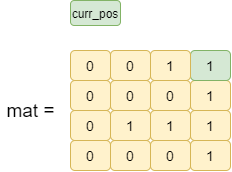
max_one_index=0

 

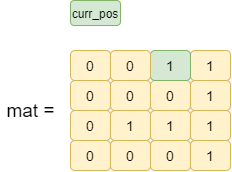
max_one_index=0

 

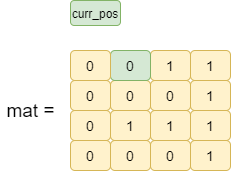
max_one_index=0

 

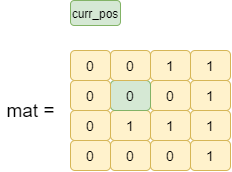
We found a 1 in the current column it means it has more 1’s than previous rows. We update the maxone_index.

max_one index=2

 

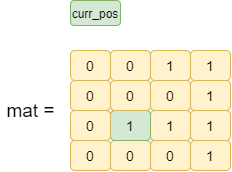
max_one_index=2

 

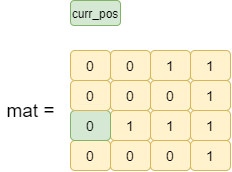
max_one_index=2

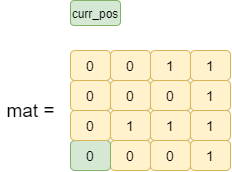
Finally, curr_pos is in the end row of the matrix. We return the max_one_index.

 

Code in C++

#include <bits/stdc++.h>
using namespace std;

int row_with_max_1s(vector<vector<int>> matrix)
{
    int max_one_index = 0; // index having maximum 1's

    int curr_pos = matrix[0].size() - 1; //initilize current position as the last column

    for (int i = 0; i < matrix.size(); i++)
    {
        while (curr_pos >= 0 && matrix[i][curr_pos] == 1)
        {
            curr_pos = curr_pos - 1;   // move towards left
            max_one_index = i;
        }
    }
    return max_one_index;
}

int main()
{
    vector<vector<int>> matrix = {
        {0, 0, 1, 1, 1},
        {0, 0, 0, 0, 1},
        {0, 0, 1, 1, 1},
        {0, 1, 1, 1, 1}
    };


    cout << row_with_max_1s(matrix);

    return 0;
}

 

Output

3

Complexity Analysis

Time Complexity: O(m+n) where m is the number of rows and n is the number of columns in the given matrix as we traverse each row and column once, i.e., the outer loop traverses each row the inner while loop traverses each column of the matrix.

Space complexity: It is O(1) as we require constant extra space.

You can also read about insertion into bst.

Frequently Asked Questions

What is a Binary search?

Binary search is an algorithm for finding a single item in a sorted list of items. It works by repeatedly dividing the portion of the list that could contain the item in half until you have reduced the number of possible locations to just one.

What is the use of Binary search?

In its most basic form, binary search is used to quickly locate a value in a sorted sequence (consider a sequence an ordinary array for now). For clarity, we'll refer to the sought value as the target value. The binary search keeps a contiguous subsequence of the starting sequence in which the target value is always found.

Conclusion

So, this article discussed a basic brute force approach, the Binary search approach, and an efficient approach that works in linear time to find the index of the row having the maximum number of 1’s by using the sorted property of the given matrix.

More suggested problems based on Matrix→ Maximum Number of Ones, Ninja and the Rows, Largest Submatrix with Equal Number of 0's and 1's, and many more.

If you are a beginner interested in coding, enroll in courses and refer to our Guided Path on the Coding Ninjas Studio platform regarding Data Structures and Algorithms, Competitive Programming, JavaScript, and many more! where you can find questions asked by all big-tech giants like Amazon, Microsoft, Google, and many more. Along with the practice of data structures, you can participate in the contests hosted on Coding Ninjas Studio!

Nevertheless, you may consider our paid courses to give your career an edge over others!

Do upvote our blogs if you find them helpful and engaging!

Happy Learning!!