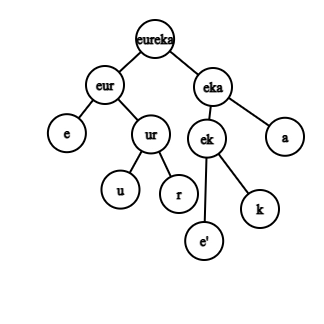
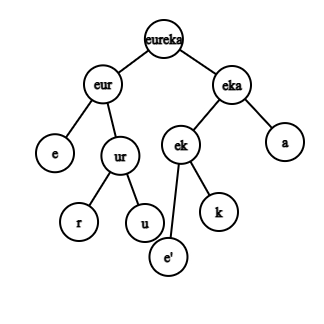
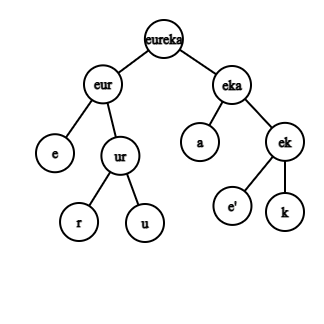
Approach 1: Using divide and conquer
Since there are many possible combinations in which the strings can be scrambled, the only way is to use recursion with Memoization to calculate the answer.
The idea is to divide the string 't' into two substrings with length 'k' and 'n-k,' where 'n' is the length of the original string 't,' and check recursively if the two substrings X = t[0….k - 1] and Y = t[k… n - 1] form some scramble to generate 's.'
Now, for t to be a scrambled form of 's,' there must be an index i, from i=1 to i=n-1, such that, at least one of these holds.
- t[0, i] scrambles into s[0, i] and t[i, N] can scramble into s[i,N].
- t[0, i] can scramble into s[i + 1, N] and t[i, N] can scramble into s[0, N - i].
Thus, if any one of these holds, we return true. Otherwise, if we're done with all this and never get true, we return false.
Since we're dividing the original string into smaller strings solving the same problem for the smaller strings, this is the Divide and conquer approach.
Another thing to note is that for two strings to be the scrambled form of each other, they also need to be each other's anagram, i.e., if we sort the strings and then compare them, they should be equal to each other. So this is one condition that we will check beforehand only.
Algorithm
-
Input the strings s and t.
-
Call the function scramble_string for the strings s and t, which returns true if s and t are scrambled form of each other, otherwise returns false.
In the function scramble_string:
-
First, check if the strings are of the same length because for the strings to be scrambled form of each other, they must be of the same length. If they're not of the same length, return false.
-
Then, write the base case. If the length of the strings is zero, they must be scrambled form of each other because the empty string can always be scrambled form of each other. Thus, return true in that case.
-
Equal strings are scrambled strings of each other. Therefore, check if both the strings are equal. If equal, then return true.
-
Check if they are an anagram of each other or not. For this, make a temporary copy of both the strings. Sort both the copies. If both the sorted strings are not equal, the strings are not an anagram of each other, and that's why there are no scrambled forms of each other, so return false.
-
Now, check for each substring. For each i, check both the conditions. Check if t[0...i] is a scrambled string of s[0...i] and if t[i+1...n] is a scrambled string of s[i+1...n]. If yes, return true. Check if t[0...i] is a scrambled string of s[n-i...n] and t[i+1...n] is a scramble string of s[0...n-i-1]. If yes, return true.
-
If none of the above conditions hold, return false.
- If the function scrambled_strings return true, print "Yes," otherwise print "No."
C++ implementation
#include <bits/stdc++.h>
using namespace std;
bool scramble_string(string s, string t)
{
/*
For the strings to be scrambled form of each other, they must be of
same length
*/
if (s.length() != t.length()) {
return false;
}
int n = s.length();
// if the strings are empty, they are scrambled form of each other
if (n == 0) {
return true;
}
// Equal strings are scramble strings of each other
if (s == t) {
return true;
}
/*
Check if they are anagram of each other or not
For this, make a temporary copy of both the strings
*/
string temp_s = s, temp_t = t;
// sort both the copies
sort(temp_s.begin(), temp_s.end());
sort(temp_t.begin(), temp_t.end());
/*
if both the sorted strings are not equal, the strings
are not anagram of each other and that's why they're
are not scrambled form of each other, so return false.
*/
if (temp_s != temp_t) {
return false;
}
/*
For each i, check both the conditions.
*/
for (int i = 1; i < n; i++) {
/*
Check if t[0...i] is a scrambled string of s[0...i]
and if t[i+1...n] is a scrambled string of s[i+1...n]
*/
if (scramble_string(s.substr(0, i), t.substr(0, i)) && scramble_string(s.substr(i, n - i), t.substr(i, n - i))) {
return true;
}
/*
Check if t[0...i] is a scrambled string of s[n-i...n]
and t[i+1...n] is a scramble string of s[0...n-i-1]
*/
if (scramble_string(s.substr(0, i),t.substr(n - i, i)) && scramble_string(s.substr(i, n - i),t.substr(0, n - i))) {
return true;
}
}
// If none of the above conditions hold true, return false
return false;
}
int main()
{
string s,t;
s="eureka";
t="eruaek";
if (scramble_string(s,t)) { // If they are scrambled form of
// each other, print yes
cout << "Yes"<<endl;
}
else {// Otherwise, print no
cout << "No"<<endl;
}
return 0;
}

You can also try this code with Online C++ Compiler
Input
eureka
eruaek

You can also try this code with Online C++ Compiler
Output
Yes

You can also try this code with Online C++ Compiler
Complexities
Time complexity
O(2^n), where n is the length of the string s and t
Reason: Each recursive call is called for the strings of length (i), (n-1). There can be total O(n) different pairs of the strings as there are total n i's from which we can split. Now, after the split, we recursively check the two substrings until they are single characters, which takes time O(2^i+2^(n-i)), where i and n-i are the lengths of the two substrings. That's why the time complexity will equal O(2^n).
Space complexity
O(2^n), where n is the length of string s and t
Reason: The space taken by the recursion stack is O(2^n) as there are 2^n function calls. All the other variables consume constant space.
Approach 2: Using dynamic programming (Memoization)
If you draw the recursion tree of an example using the above solution, you will notice that there are some pairs of substrings of s and t, for which we're calculating the answer more the one time. This increases the time complexity.
To avoid this, we can remember the answer of the pair of a substring of s and t when we calculate it for the first time. If we do this, we don't have to calculate the answer for the same pair of substrings again ever. Thus, this reduces the time complexity. This approach is called the dynamic programming approach(Memoization).
We will store the answer of the pair of substrings of s and t in a map. The answer will be of type boolean.
Algorithm
-
Input the string s and t
-
Declare a map with key as a pair of two strings and value of type boolean named "mp."
-
Call the function scramble_string for the strings s, and t, which returns true if s and t are scrambled form of each other otherwise returns false. In the function scramble_string:
-
First, check if the strings are of the same length or not because for the strings to be scrambled form of each other, they must be of the same length. If they're not of the same length, return false.
-
Then, write the base case. If the length of the strings is zero, they must be scrambled form of each other because the empty string can always be scrambled form of each other. Thus, return true in that case.
-
Equal strings are scramble strings of each other. Therefore, check if both the strings are equal and true if yes.
-
Check if they are an anagram of each other or not. For this, make a temporary copy of both the strings. Sort both the copies. If both the sorted strings are not equal, the strings are not an anagram of each other, and that's why there are no scrambled forms of each other, so return false.
-
Now, check if we've already calculated the answer for this pair of strings. For this, find the pair {s,t} in the map, if it is present , return mp[{s,t}]. Otherwise, move on to the next step.
-
Now, check for each substring. For each i, check both the conditions. Check if t[0...i] is a scrambled string of s[0...i] and if t[i+1...n] is a scrambled string of s[i+1...n]. If yes, update mp[{s,t}] = true, and return true. Check if t[0...i] is a scrambled string of s[n-i...n] and t[i+1...n] is a scramble string of s[0...n-i-1]. If yes, update mp[{s,t}] = true, and return true.
-
If none of the above conditions hold true, update mp[{s,t}] = false and return false.
- If the function scrambled_strings returns true, print "Yes," otherwise print "No."
C++ implementation
#include <bits/stdc++.h>
using namespace std;
map<pair<string,string>,bool>mp;
bool scramble_string(string s, string t)
{
/*
For the strings to be scrambled form of each other, they must be of
same length
*/
if (s.length() != t.length()) {
return false;
}
int n = s.length();
/*
if the strings are empty, they are scrambled form of each other
*/
if (n == 0) {
return true;
}
/*
Equal strings are scramble strings of each other
*/
if (s == t) {
return true;
}
/*
Check if they are anagram of each other or not
For this, make a temporary copy of both the strings
*/
string temp_s = s, temp_t = t;
// sort both the copies
sort(temp_s.begin(), temp_s.end());
sort(temp_t.begin(), temp_t.end());
/*
if both the sorted strings are not equal, the strings
are not anagram of each other and that's why they're
are not scrambled form of each other, so return false.
*/
if (temp_s != temp_t) {
return false;
}
/*
Check if we've already calculated the answer for this pair
of string
*/
if(mp.find({s,t})!=mp.end()){ // If yes, return mp[{s,t}]
return mp[{s,t}];
}
/*
For each i, check both the conditions.
*/
for (int i = 1; i < n; i++) {
// Check if t[0...i] is a scrambled string of s[0...i]
//and if t[i+1...n] is a scrambled string of s[i+1...n]
if (scramble_string(s.substr(0, i), t.substr(0, i)) && scramble_string(s.substr(i, n - i), t.substr(i, n - i))) {
return mp[{s,t}] = true;
}
// Check if t[0...i] is a scrambled string of s[n-i...n]
//and t[i+1...n] is a scramble string of s[0...n-i-1]
if (scramble_string(s.substr(0, i),t.substr(n - i, i)) && scramble_string(s.substr(i, n - i),t.substr(0, n - i))) {
return mp[{s,t}] = true;
}
}
/*
If none of the above conditions hold true, return false
*/
return mp[{s,t}] = false;
}
int main()
{
string s,t;
s="eureka";
t="eruaek";
if (scramble_string(s,t)) { // If they are scrambled form of
// each other, print yes
cout << "Yes"<<endl;
}
else {// Otherwise, print no
cout << "No"<<endl;
}
return 0;
}

You can also try this code with Online C++ Compiler
Input
eureka
eruaek

You can also try this code with Online C++ Compiler
Output
Yes

You can also try this code with Online C++ Compiler
Complexities
Time complexity
O(n^2), where n is the length of the string s and t
Reason: Each recursive call is called for the strings of length (i), (n-1). That's why the total number of calls will be n^2, making the time complexity equal to O(n^2).
Space complexity
O(n^2), where n is the length of string s and t
Reason: The space taken by the map here is equal to the number of recursive calls which is equal to n^2. Thus, space complexity is (n^2).
Approach 3: Bottom-up Dynamic programming
We can further optimize the space complexity of the above solution, but the time complexity will also increase using the bottom-up dynamic programming approach. In this approach, we will build the solution of the smallest cases and then keep building the larger cases answers using the smaller cases answers.
We store the answer of the different cases in a 3D dp vector. Here, dp[i][j][k] will be true if t.substr(j,k) is a scrambled form of s.substr(i,k). Now, the base case will be when k is 1, i.e., the length of the substrings is 1. Thus, for each pair of (i,j) will calculate the answer of dp[i][j][1]. Dp[i][j][1] will be true if s[i]==t[j], otherwise, false. Now, for the further cases, dp[i][j][k] will be true, if for any z from 1 to k-1, (dp[i][j][z]==true && dp[i+z][j+z][k-z]==true) or (dp[i][j+(k-z)][z]==true && dp[i+z][j][k-z]==true) because dp[i][j][k] can be be true only if we can find a point z from where we can cut the k length string into two pieces which are both scrambled form of each other.
Algorithm
-
Input the string s and t
-
Declare a map with key as a pair of two strings and value of type boolean named "mp."
-
Call the function scramble_string for the strings s, and t, which returns true if s and t are scrambled form of each other otherwise returns false. In the function scramble_string:
-
If the size of the string s and t is not originally the same, return false.
-
If the size of the string s and t is 0, return true.
-
Otherwise, create a 3D DP vector of size nxnx(n+1), where n is the size of the string s and t.
-
Initialize the dp vector with values false.
-
Calculate the answers for the base cases, i.e., for the cases when k is 1. Run two nested for loops for the different i and j value and calculate the answer for dp[i][j][1]. Dp[i][j][1] will be true if s[i]==t[j].
-
For the other cases, run four nested loops. The first one will be from k=2 to k<=n as this is the length of the substrings possible. The second one will be from i=0 to i+k<=n, as i is the starting index of the substrings of string s with a length equal to k. The third one will be from j=0 to j+k<=n, as j is the starting index of the substrings of string t with a length equal to k. The fourth one will be from z = 1 to z<k as z denotes the different cutting points at which we're cutting the strings of length k.
-
Inside the fourth loop write the recurrence relation as, dp[i][j][k] = ((dp[i][j][z]==true && dp[i+z][j+z][k-z]==true) || (dp[i][j+(k-z)][z]==true && dp[i+z][j][k-z]==true)).
-
Return dp[0][0][n].
- If the function scrambled_strings return true, print "Yes," otherwise print "No."
C++ implementation
#include <bits/stdc++.h>
using namespace std;
bool scramble_string(string s, string t)
{
/*
For the strings to be scrambled form of each other, they must be of
same length
*/
int n = s.length();
// if the strings are empty, they are scrambled form of each other
if (n == 0) {
return true;
}
// Declare and initialize the vector dp with value false.
vector<vector<vector<bool> > > dp (n, vector<vector<bool>>(n, vector<bool>(n + 1, false)));
// calculate the answer for base cases
for (int i = 0; i < n; ++i){
for (int j = 0; j < n; ++j){
dp[i][j][1] = (s[i] == t[j]);
}
}
for (int k = 2; k <= n; ++k){
for (int i = 0; i + k <= n; ++i){
for (int j = 0; j + k <= n; ++j){
for (int z = 1; z < k; ++z){
int z2 = k - z;
// Recurrence relation
// two substrings are not swapped
if (dp[i][j][z] && dp[i+z][j+z][z2]){
dp[i][j][k] = true;
}
// two substrings are swapped
if (dp[i][j + z2][z] && dp[i + z][j][z2]){
dp[i][j][k] = true;
}
}
}
}
}
return dp[0][0][n];
}
int main()
{
string s,t;
cin>>s>>t; // Input the string s and t
if (scramble_string(s,t)) {
/*
If they are scrambled form of
each other, print yes
*/
cout << "Yes"<<endl;
}
else {
// Otherwise, print no
cout << "No"<<endl;
}
return 0;
}

You can also try this code with Online C++ Compiler
Input
eureka
eruaek

You can also try this code with Online C++ Compiler
Output
Yes

You can also try this code with Online C++ Compiler
Complexities
Time complexity
O(n^4), where n is the length of the string s and t
Reason: The four nested loops take O(n^4) time.
Space complexity
O(n^3), where n is the length of string s and t
Reason: Space taken by the DP array is n^3.
Frequently Asked Questions
What are the Divide and Conquer algorithms?
The Divide and Conquer (or DAC) is an algorithm that solves a very big task or a problem by breaking it into smaller sub-tasks or sub-problems; after solving, we combine all the sub-tasks in a specific manner so that we get the result for the big task.
What is the difference between Divide and Conquer and Dynamic Programming (DP)?
The DAC algorithm and DP (or Memoization) divide a big task into smaller sub-tasks. But the major difference between these two is that the DP algorithm saves the result of the sub-problems to be utilized in the future, but in the case of DAC, the sub-tasks are further solved recursively and are not saved for future reference.
What are the disadvantages of the Divide and conquer algorithm?
Most of the algorithms that use the DAC approach are implemented using recursion, making them costly in memory management. Stack space for recursive calling increases the space complexity. The DAC approach is challenging to implement when the sub-problems are not similar.
What is dynamic programming, and where is it used?
Dynamic programming is an optimization method used in various programming problems. It is used in problems where the solution depends on smaller overlapping subproblems. We use it to memorize the results to use them later when needed.
Conclusion
This article discussed the solution to the scramble string problem using the Divide and conquer algorithm. One of the efficient solutions to this problem was based on the concept of dynamic programming. This is one of the very interesting and crucial topics, and problems based on this are asked during various coding contests as well as placements tests.
We suggest you solve more problems based on this.
Some of these are Maximum profit, Longest Common prefix, wildcard pattern matching, and rod cutting problem.
If you want to understand the Divide and conquer algorithm and where it is used, check out Divide and Conquer Notes in Guided Paths.
Some of the problems are count inversions, longest common prefix, reverse pairs, median of two sorted arrays, wrong turn, and ninjas and ladoos.
Are you planning to ace the interviews of reputed product-based companies like Amazon, Google, Microsoft, and more?
Attempt our Online Mock Test Series on Coding Ninjas Studio now!
Happy Coding!