Introduction-
In the previous blog on the rotated sorted array, we learned about searching in the rotated sorted array with no duplicate elements. In this blog, we will learn about searching an element in a rotated sorted array with duplicate elements. But before diving into the solution, let's see an example and understand the problem thoroughly-
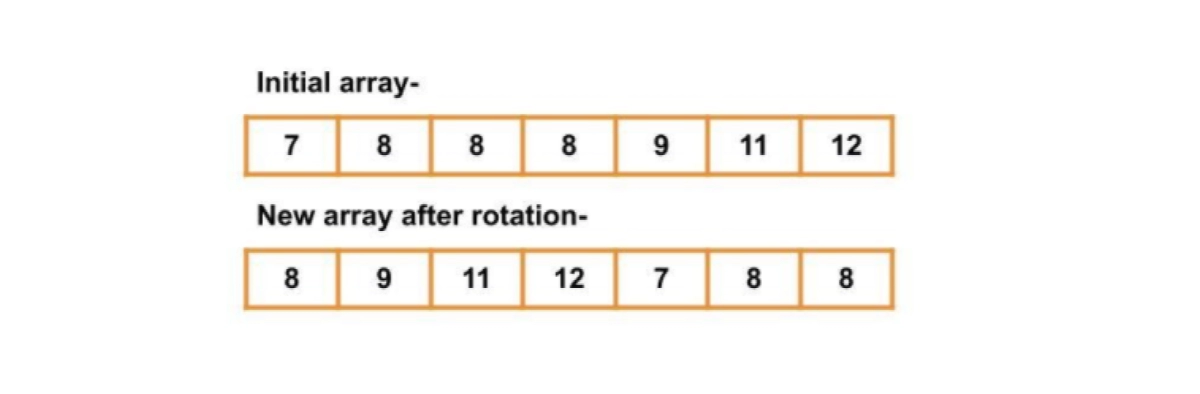
The array given above is sorted from the 8 at the 0th index to 12 and 7 to 8 at the last index. Or we can say that it was a sorted array from 7 to 12, then rotated by three positions in the clockwise direction. Now we have the task of searching the given number in this array. Let's see how we can do that-
Recommended Topic, Array Implementation of Queue and Rabin Karp Algorithm
Solution using modified binary search-
The idea to solve this problem is very similar to what we used for searching an element in a rotated sorted array with no duplicate elements. We used a modified binary search for this.
We start with finding the mid element of the array, divide the array into two subarrays around that middle element, and then pick one subarray to follow the above process recursively. Now we know that for a rotated sorted array, one of the subarrays is sorted. So, we compare the left, right, and mid-value to check which sub-array is sorted.
At this step in the rotated sorted array with duplicate elements, all three values left, middle, and right elements could be the same. Then, we won't be able to decide which subarray is sorted. For Example:Let nums = [4 5 6 4 4 4 4] ,mid = 3 and lo = 0, since nums[3] >= nums[0] but the array from 0 to 3 is out of order and not sorted, so we need to modify the previous solution to handle this case.
To accommodate the case of left, right, middle elements being equal, we can put a check for this before checking which subarray is sorted. And if all these elements are equal, we will move the left and right counters inwards by one position at a time to find a subarray with different values at the left and right index. let's see an example to develop a better understanding-
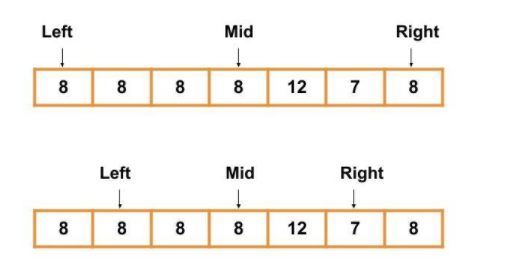
In the above example, the left, middle and right elements are equal, so we can't decide which subarray is sorted. But, if we move both the left and right counters one position inwards(i.e left = left +1 and right = right - 1), the value of right changes to 7, and we can find that the left subarray is sorted.




