Sample Examples
Example 1
Input

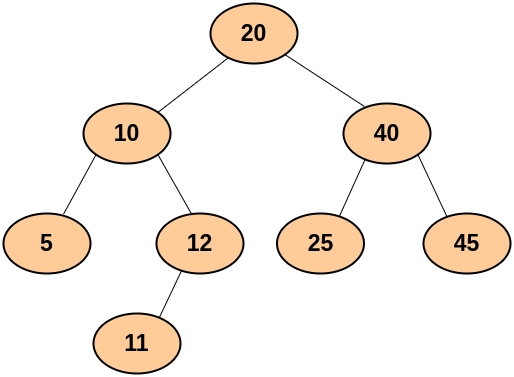
Output

Explanation
Node with value 25 is present in our binary search tree.
Recursive Approach
We’ll visit the root node and will check if its value is equal to the required value or not. If it’s not then, we’ll move to the right or left subtree and will repeat the same process.
We’ll move to the left subtree if the required value is smaller than the root, otherwise, we’ll move to the right subtree.
Algorithm
ALGO_SEARCH(ROOT, VAL):
if ROOT is NULL:
return False
if ROOT > VAL:
return ALGO_SEARCH(ROOT->left, VAL)
else
return ALGO_SEARCH(ROOT->right, VAL):
Implementation in C++
#include <bits/stdc++.h>
using namespace std;
class Node
{
public:
int data;
Node *left, *right;
Node(int val){
data = val;
left = right = nullptr;
}
};
bool presentOrNot(Node *root, int value) {
if(root == nullptr) return false;
// value is present in our binary search tree
if(root->data == value) return true;
// move to the left subtree if value is smaller than root
// else move to the right subtree
if(root->data > value) return presentOrNot(root->left, value);
else return presentOrNot(root->right, value);
}
Node *insertData(Node *root, int data) {
// tree is empty, return new node
if (root == nullptr) return new Node(data);
// recurr the tree to find the position where
// data needs to be inserted
if (data < root->data) root->left = insertData(root->left, data);
else if (data > root->data) root->right = insertData(root->right, data);
// return the root node
return root;
}
int main(){
// creating binary search tree
Node *root = nullptr;
root = insertData(root, 20);
insertData(root, 10);
insertData(root, 5);
insertData(root, 12);
insertData(root, 11);
insertData(root, 40);
insertData(root, 25);
insertData(root, 45);
int valueToSearch = 25;
// printing the result
cout << "Node with " << valueToSearch << " is ";
if (presentOrNot(root, 25)) cout << "Present";
else cout << "Not Present";
cout << " in our binary search tree." << endl;
return 0;
}

You can also try this code with Online C++ Compiler
Output
Node with 25 is Present in our binary search tree.
Time Complexity ⌛

The time complexity of the above approach is O(N), where N is the number of nodes in the binary search tree. This is when the binary search tree is not balanced (skewed). However, if it is given that the BST is balanced, then the time complexity would be O(logN), where N is again the number of nodes in the tree.
Space Complexity 🚀

The space complexity of the above program is O(N) due to the size of the recursion stack.
Must Read Recursive Binary Search.
Read More - Time Complexity of Sorting Algorithms
Iterative Approach
The only difference between iterative and recursive approaches is the implementation. The approach and steps will remain the same. However, we will see that the iterative approach use less space as compared to the recursive approach.
Algorithm
ALGO_SEARCH(ROOT, VAL):
while ROOT is not null:
do
if ROOT.Value is equal to VAL:
print "Value present in binary search tree"
RETURN;
if ROOT.Value > VAL:
ROOT <= ROOT.left
else:
ROOT <= ROOT.right
EXIT_LOOP
PRINT "Value not present";
Implementation in C++
#include <bits/stdc++.h>
using namespace std;
class Node
{
public:
int data;
Node *left, *right;
Node(int val){
data = val;
left = right = nullptr;
}
};
bool presentOrNot(Node *root, int value)
{
// loop to traverse binary search tree
while (root != nullptr)
{
// return true if value if found
if (root->data == value)
{
return true;
}
// change root to left subtree if value is greater than root
// else change it to right subtree
if (root->data > value)
{
root = root->left;
}
else
{
root = root->right;
}
}
// if true is not returned from the above loop
// it means value is not present in our binary search tree
return false;
}
Node *insertData(Node *root, int data) {
// tree is empty, return new node
if (root == nullptr) return new Node(data);
// recur the tree to find the position where
// data needs to be inserted
if (data < root->data) root->left = insertData(root->left, data);
else if (data > root->data) root->right = insertData(root->right, data);
// return the root node
return root;
}
int main(){
// creating binary search tree
Node *root = nullptr;
root = insertData(root, 20);
insertData(root, 10);
insertData(root, 5);
insertData(root, 12);
insertData(root, 11);
insertData(root, 40);
insertData(root, 25);
insertData(root, 45);
int valueToSearch = 25;
// printing the result
cout << "Node with " << valueToSearch << " is ";
if (presentOrNot(root, 25))
cout << "Present";
else
cout << "Not Present";
cout << " in our binary search tree." << endl;
return 0;
}

You can also try this code with Online C++ Compiler
Output
Node with 25 is Present in our binary search tree.
Time Complexity ⌛

The time complexity of the above approach is O(logN) if the given BST is balanced. In case of not balanced or skewed BST, the time complexity of the above program would be O(N), where N is the number of nodes in our tree.
Space Complexity 🚀

No extra space is used. So, the space complexity of the above program is O(1).
Frequently Asked Questions ⁉️

What is a binary tree?
A binary tree is a tree data structure having a maximum of two children. There can only be two children per element in a binary tree, hence we usually refer to them as the left and right children.
What is a binary search tree?
A binary search tree is a type of binary tree in which all of the nodes left to the root node have values less than the root node and all of the nodes right to the root node have values greater than the root node.
What is a Full Binary Tree?
A full binary tree is a particular kind of binary tree in which every parent node and internal node either has two children or none at all.
Conclusion
In this article, we have discussed a coding problem in which we have to search for a key in BST. We have seen two different implementations - Iterative and Recursive. We found out that though the time complexities remained the same, the iterative approach performs better in terms of space complexity.
If you think this blog has helped you enhance your knowledge about the above question, and if you would like to learn more, check out our articles
and many more on our website.
Check out this problem - Connect Nodes At Same Level
Visit our website to read more such blogs. Make sure that you enroll in the courses provided by us, take mock tests and solve problems available and interview puzzles. Also, you can pay attention to interview stuff- interview experiences and an interview bundle for placement preparations. Do upvote our blog to help fellow ninjas grow.

Please upvote our blog if you find them interesting to help other ninjas grow.
Happy Learning!












