Table of contents

Introduction

1.1.

What are Set Operations

Union of sets

Intersection of sets

Complement of Sets

Set Difference

FAQ’S

Key Takeaways

Last Updated: Mar 27, 2024

Easy

Set Operations

Author Soumya Agrawal

Introduction

A set is defined as a collection of elements. Each object inside a set is referred to as an 'Element.' A set can be represented in different forms.

statement form
roster form
set-builder form.

What are Set Operations

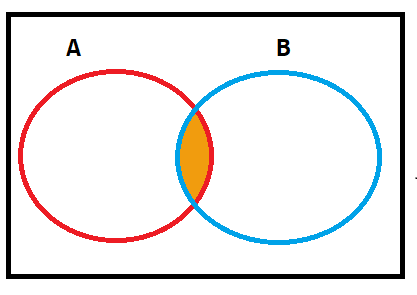
When we want to establish the relationship between the sets, there comes the concept of set operations. Set operations(union, intersection, etc.) are performed on two or more sets to get through the combination of elements.

Four primary set operations that are performed on sets are:

Intersection of sets
Union of sets
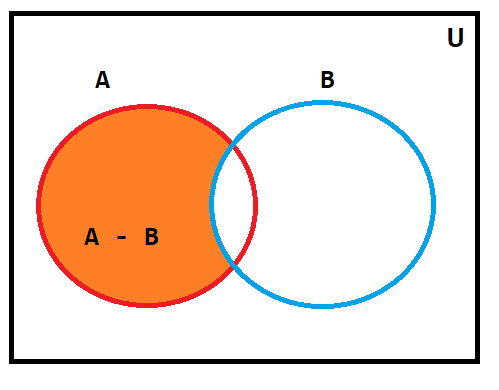
Difference of sets
Complement of sets

Before discussing the set operations in detail, let's look at the Venn diagram first, which will help you understand the working of operations appropriately.

John Venn invented the Venn diagram, a logical diagram that shows all possible logical combinations between different sets.

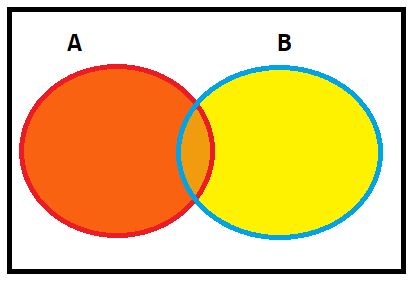
Union of sets

We are provided with two sets, A and B, then the union of A and B(A U B) is the set of distinct elements that belong to set A and B or both.

Let us take an example to understand this operation clearly.

Set A = {2,5,7}

Set B = {2,5,6}

The union of set, A U B={2,5}

Intersection of sets

We are given two sets, A and B, then the intersection of A and B(denoted by A ∩ B) is the subset of the universal set U, which consists of elements common to both A and B.

If A = { 1, 5, 6} and B = { 1, 4, 6, 7 }, then A ∩ B = { 1, 6 }.

Complement of Sets

The complement of a set, say A (denoted as A′ or Ac), is the set of all the elements in the given universal set(U) that are not present in set A. Let us consider an example to understand this set operation of the complement of sets better,

If U = {4,5,6,7,8,9,10} and A = {4,5,6}, then A' = {7,8,9,10}.

Set Difference

We are given two sets, A and B, then the difference between these two sets is denoted as A - B, which means elements present in A but not in B.

Let's take an example to explain this operation.

A= {2,6,7,8,9}

B= {8,9}

Set difference, A - B={2,6,7}

We can also say that the difference between set A and set B equals the intersection of set A with the complement of set B. Hence,

A−B = A∩B'

The set difference can be depicted through this Venn diagram given below.

Note:

Some related topics on set operations are:

Subset
Powerset
Superset

FAQ’S

1). What are the properties of sets?

The properties of set operations are similar to the properties of fundamental operations on numbers. Some important properties are:

Associative property
Commutative Property
Distributive Property

2). What do you mean by Venn diagrams?

Venn diagrams are the pictorial representations of relationships among things or finite groups of things.

3). How Do We Use Set Operations in Real Life?

Sets are the collection of elements that helps to list all the states in the country, a list of natural numbers in a particular range. These are some real-life examples of set operations.

4). What are disjoint sets?

When the two sets have no elements in common, they are said to be disjoint sets.