Approach
We know that in the string s, if s[0…j] is a palindrome, we can add reversed s[j+1…] in the beginning to make the s palindrome.
So our target is to find the maximum j such that s[0..j] is a palindrome.
Naive approach
1. In the naive approach, we can check if the string is palindrome for every j.
2. We can know the maximum j such that the string s[0…j] is a palindrome.
3. After that, we can add the reversed s[j+1..n-1] to the beginning and return the answer.
Efficient approach
Let s1 represent the string S, and s2 represent the reversed string S.
Using z function
We can efficiently find the index j. For the substring to be a palindrome, it must be read the same forwards and backwards. Also, the substring should start from the beginning of the given string S.
The z_function gives us the length of the largest prefix of the suffix starting at i, which is also a prefix of S.
So if we want the find the largest palindrome, it should have the same z[i] as the left of the string. That is if we find out the largest z[i] such that z[i]=len(z)-i, then we get the length of the substring.
The reason is as follows. Suppose z[i]=len(z)-i means that s2[i…len(s2)] is same as s[0….len(s2)-i]. Thus we know that s[0….len(s2)-i] is a palindrome because s2 is the reversed string S.
s2[i…len(s2)-1]=s[0….len(s2)-i] implies
s2[i]=s[len(s2)-i-1] since they are reversed string(s2= reversed (s)) and s2[i]=s[0] thus s2[i]=s[len(s2)-i-1]=s[0]
Thus we get the following
1. s[len(s2)-i-1]=s[0]
2. s[len(s2)-i-2]=s[1]
3. s[len(s2)-i-3]=s[2]
And so on.
Thus we conclude that s[0….len(s2)-i] is the palindrome.
Let us see the above using an example.
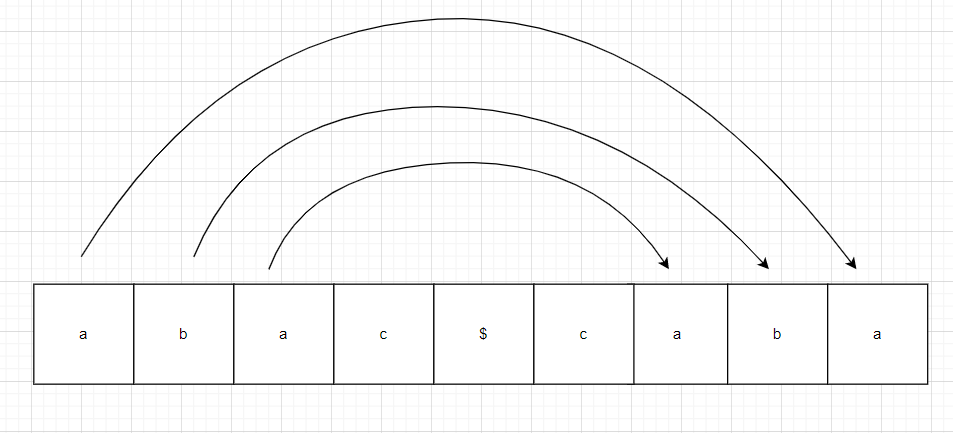
Figure 1: Matching of abac$caba using z function
Here the z function in the string “abac$caba” will be [0,0,1,0,0, 0, 3, 0, 1]. Here 3 shows that the “aba” prefix matches with the prefix at i=7(1 based indexing) “aba”. Thus we get that s[0…2]=”aba”=s[7…9]. Thus the length of the substring “aba” is 3.
In this way, we can find such palindromes and calculate the maximum length of those palindromes.
Using LPS array
Note: lps_array gives us the proper prefix which is also a suffix
Here we can easily find the length of the palindromic substring starting at the end.
The lps_array[-1] or the end element of lps_array directly gives us the length of the substring. This is because lps[-1] or lps.back() or the end element of lps_array gives us the proper prefix which is also a suffix. So S[0…length] = S1[len(s1)-length….len(S1)] and since the end array is actually reversed initial array, we conclude that the S[0…length] = S[length….0].
Thus we find the length of the largest starting substring which is also a palindrome.
Pseudocode
Approach 1: LPS Array
DEFINE FUNCTION get_lps(search):
lps_arr=[0 FOR i IN range(len(search))]
previous=0
curr_index=1
WHILE curr_index<len(lps_arr):
IF search[curr_index]==search[previous]:
previous+=1
lps_arr[curr_index]=previous
curr_index+=1
ELSEIF previous==0:
lps_arr[curr_index]=0
curr_index+=1
ELSE:
# we replace current_index
previous=lps_arr[previous-1]
RETURN lps_arr
DEFINE FUNCTION get_palindrome(s1):
s=s1+"#"+s1[::-1]
lps_array=get_lps(s)[len(s)//2+1:]
# OUTPUT(lps_array)
IF lps_array:
ans=lps_array[-1]
ELSE:
ans=0
theta=s1[ans:]
RETURN theta[::-1]+s1
Approach 2: Using the z algorithm
DEFINE FUNCTION z_function(S):
l=0
r=0
SET n TO len(S)
# initializing the z algorithm by 0 initially
SET z TO [0 FOR i IN range(n)]
FOR i IN range(1, n):
IF i<=r:
z[i]=min(r-i+1,z[i-l])
# OUTPUT(z)
WHILE i+z[i]<n and S[z[i]]==S[i+z[i]]:
z[i]+=1
IF i+z[i]-1>r:
l=i
r=i+z[i]-1
# OUTPUT(z)
SET z[0] TO n
RETURN z
z_function("aaaabaaaa")
DEFINE FUNCTION get_palindrome(s1):
"""
adding # as a separator
"""
s=s1+"#"+s1[::-1]
# finding z function of the reversed string
z=z_function(s)[len(s)//2+1:]
OUTPUT(z)
maxa=0
FOR i IN range(len(z)):
IF z[i]==len(z)-i:
maxa=z[i]
# OUTPUT(maxa)
break
ans=maxa
""" as the length is answer we slice the substring which is not the palindrome
Here s1[:ans] is the palindrome
so we do not have to add it again
"""
theta=s1[ans:]
# we add the reversed of theta to the s1 IN the beginning to make it palindrome
# thus theta[::-1] are the characters to make it palindrome
RETURN theta[::-1]+s1
Also read, Application of Graph in Data Structure
Code in Python
Approach 1: Using the z algorithm
def z_function(S):
l=0
r=0
n = len(S)
# initializing the z algorithm by 0 initially
z = [0 for i in range(n)]
for i in range(1, n):
if i<=r:
z[i]=min(r-i+1,z[i-l])
# print(z)
while i+z[i]<n and S[z[i]]==S[i+z[i]]:
z[i]+=1
if i+z[i]-1>r:
l=i
r=i+z[i]-1
# print(z)
z[0] = n
return z
z_function("aaaabaaaa")
def get_palindrome(s1):
"""
adding # as a separator
"""
s=s1+"#"+s1[::-1]
# finding z function of the reversed string
z=z_function(s)[len(s)//2+1:]
maxa=0
for i in range(len(z)):
if z[i]==len(z)-i:
maxa=z[i]
# print(maxa)
break
ans=maxa
""" as the length is answer we slice the substring which is not the palindrome
Here s1[:ans] is the palindrome
so we do not have to add it again
"""
theta=s1[ans:]
# we add the reversed of theta to the s1 in the beginning to make it palindrome
# thus theta[::-1] are the characters to make it palindrome
return theta[::-1]+s1
s="aabbaabb"
palindrome=get_palindrome(s)
print(palindrome)

You can also try this code with Online Python Compiler
Approach 2: Using LPS array
def get_lps(search):
# lps array is the longest proper prefix which is also a suffix
lps_arr=[0 for i in range(len(search))]
# previous is the last longest proper prefix which is also a suffix
previous=0
# Here we are checking proper prefix so that we start with the index 1
# as the prefix can't be itself
curr_index=1
while curr_index<len(lps_arr):
if search[curr_index]==search[previous]:
"""This means that we have found a match for the last longest lps
and the current prefix
Thus we update the lps array"""
previous+=1
lps_arr[curr_index]=previous
curr_index+=1
elif previous==0:
"""This means that we have not found a match for the current prefix with the
last lps.
As previous=0 then there does not exist previous longest lps."""
# no lps[curr index] exist so lps[curr_index]=0
lps_arr[curr_index]=0
curr_index+=1
else:
# we replace current_index
previous=lps_arr[previous-1]
return lps_arr
def get_palindrome(s1):
"""
adding the "#" and the reversed s1 to the s.
thus s= s1 + "#" + string form of reversed(s1)
"""
s=s1+"#"+s1[::-1]
lps_array=get_lps(s)[len(s)//2+1:]
# print(lps_array)
if lps_array:
ans=lps_array[-1]
else:
ans=0
""" as the length is answer we slice the substring which is not the palindrome
Here s1[:ans] is the palindrome
so we do not have to add it again
"""
theta=s1[ans:]
# we add the reversed of theta to the s1 in the beginning to make it palindrome
# thus theta[::-1] are the characters to make it palindrome
return theta[::-1]+s1
s="aabbaabb"
palindrome=get_palindrome(s)
print(palindrome)

You can also try this code with Online Python Compiler
Input
aabbaabb
Output
bbaabbaabb
Time Complexity
The time complexity for both approaches is O(N).
For approach 1, we are finding lps_array, which takes O(N) time. From that LPS array, we know the length of the substring that is to be reversed and added.
For approach 2, the z-function also takes O(N) time. Similarly, we can know the length of the substring, which is to be reversed and added from the z_array.
Space Complexity
The space complexity for both approaches is O(N).
For the LPS approach, we are making an LPS array of size O(N).
For the z-function approach, we are making a Z function array of size O(N).
Also see, Morris Traversal for Inorder and Rabin Karp Algorithm
You can also read about Palindrome Number in Python here.
Frequently Asked Questions
1. What is the time complexity of the naive algorithm?
For the brute force algorithm, we have to find the largest palindrome substring starting from index 0 in the given string. Thus we will check for N palindromes in the worst case. Therefore the worst-case time complexity is O(N*N).
2. What would be the space complexity of the naive algorithm?
The space complexity of the naive algorithm is O(1) if we exclude the input and output strings. The reason is that we are using no extra space in checking palindrome.
3. How does the z function help us optimise the code?
Using the z algorithm, we get the matches in the reverse string with the original array. Thus, we can know the length of the largest palindrome starting at index 0. By knowing the size of the substring, we can easily calculate the front characters to be added.
4. Why are we adding “#” in the new string?
The # is added to separate the original string and the new string. As we want to find the longest palindrome between the original string and the new one, we need to separate them by some unused characters not present in the original string.
5. What is s1[::-1] in the code?
s1[::-1] represents the reversed string of s1. It creates a new string of the same length but assigns the characters of s1 in the reversed order.
Key Takeaways
The article helps us understand how the KMP algorithm and z function helps us find the string palindrome by adding minimum characters in the beginning. Comments have been added to the code for better understanding. Print statements have been added in the comments. So by uncommenting them, we can print the z array and the LPS array. You can also copy the code and run it on your system on multiple inputs to understand the approach better.
If you would like to practice more, do try the Longest Palindromic Subsequence problem.
Check out Coding Ninjas Studio to learn more about competitive programming, DSA, attempt mock tests, interview preparation and much more.
Happy Learning!!!





