What is SVD used for?

Singular Value Decomposition (SVD) is a widely used technique to decompose a matrix into several component matrices, exposing many of the useful and interesting properties of the original matrix.

Does SVD always exists?

Yes, SVD always exists for any square and rectangular matrix.

What is an advantage of SVD?

SVD helps simplify data, removing noise from the data; it is also used for representing the dataset in simple and reduced form.

Table of contents

Introduction

Mathematical Equation

2.1.

Example

Applications of SVD

3.1.

Calculating pseudo-inverse

3.2.

Rank, Range, and Null Space

3.3.

Curve Fitting Problems

Implementation

4.1.

Image compression using SDV

Frequently Asked Questions

Key Takeaways

Last Updated: Mar 27, 2024

Singular Value Decomposition

Author soham Medewar

Introduction

Singular Value Decomposition(SVD) is simply the factorization of the matrix. A given matrix is broken down into three matrices such that their dot product is equal to the original matrix. SVD is the most widely used method for matrix decomposition. SVD has its application in data reduction, data compression, etc. Furthermore, we will discuss its mathematical method, code, and an example.

Mathematical Equation

Let us consider a matrix A of dimension m×n. As shown below, we can break matrix A into three matrices U, Σ, and V.

A = U . Σ . V^T

(V^T represents the transpose of the matrix V)

Here the dimensions of U are m×m, the dimensions of Σ are m×n, and the dimensions of V are n×n.

Matrix U is also called the left singular vectors of matrix A, and V is called the right singular vectors of matrix A. The Σ is known as the sigma matrix. The sigma matrix is the diagonal matrix.

U is a matrix of the orthonormal eigenvectors of AA^T.
VT is a matrix of the orthonormal eigenvectors of A^TA.
Σ is matrix having singular values, which are the square roots of the eigenvalues of A^TA.

Example

Let us under SVD by an example.

Consider a matrix A find SVD of the matrix A.

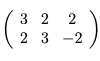
The first step for finding the SVD is to calculate the singular values 𝜎_i by finding eigenvalues of AA^T.

AA^T =

The characteristics polynomial will be:

AA^T - λI= 0

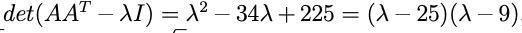
Therefore, we will get:

λ² - 34λ + 225 = 0

Eigen values will be 9, 25.

Singular values = sqrt(9), sqrt(25) i.e, 3, 5.

𝜎₁= 5, 𝜎₂ = 3.

Furthermore, we will find the right singular vectors by finding an orthonormal set of eigenvectors of A^TA. The eigenvalues will be 0, 9, 25. As A^TA is symmetric, the eigen vectors will be orthogonal.

For λ = 25, we have

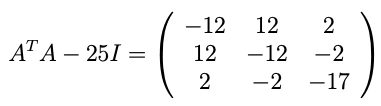
which is row-reduced to:

A unit length vector in that direction is:

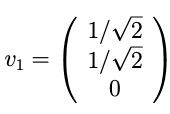
Similarly, we will calculate the unit length vector for λ = 9.

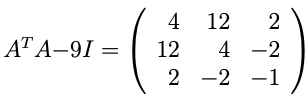
which is row-reduced to:

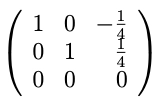
A unit length vector in that direction is:

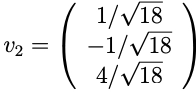
For the last eigenvector, we can find the unit vector perpendicular to v₁ and v₂.

v₁^T.v_3. = 0

v₂^T.v_3. = 0

Solving the equations we get.

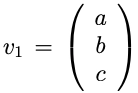
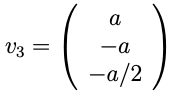
Therefore, v₃ equals to:

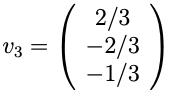
Till now, we know sigma and V^T.

We can calculate U by using the following formula u_i = 1/σ(Av_i)

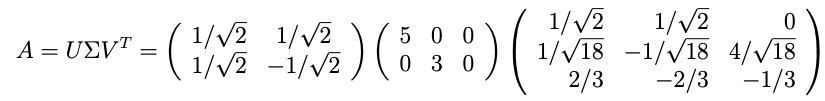
Hence matrix A is factorized into three matrices.

Applications of SVD

Calculating pseudo-inverse

SVD is used to calculate the pseudo inverse or Moore-Penrose inverse. It is a generalization of the matrix inverse that may not be invertible. If the matrix is not invertible, then it's pseudo-inverse exists, and if the matrix is invertible, its inverse is equal to pseudo-inverse. It is denoted by A^T.

Methods to the pseudo-inverse of a matrix.

Let us consider a matrix A.

SVD of a matrix can be written as:

A = U . Σ . V^T

Multiplying both sides by A^-1.

A^-1A = A^-1.U . Σ . V^T

I = A^-1.U . Σ . V^T

Now, multiply both sides by V

V = A^-1.U . Σ . V^TV

V = A^-1.U . Σ

Now, multiply by Σ^-1, as Σ is singular matrix its inverse will be:

diag(a₁, a₂, a₃, a₄, ….)^-1

diag(1/a₁, 1/a₂, 1/a₃, 1/a₄, ….)

V . Σ^-1 = A^-1.U . Σ . Σ^-1

V . Σ^-1 = A^-1.U

Now, multiply by U^T.

V . Σ^-1 . U^T = A^-1.U . U^T

V . Σ^-1 . U^T = A^-1

The above equation qives pseudo-inverse.

Rank, Range, and Null Space

The rank of the matrix can be calculated by using SVD. Counting the number of non-zero singular values.
The range of matrix A is the left singular vectors of U corresponding to singular non-zero values.
The right singular vectors of matrix V corresponding to zeroed singular values represent the Null Space of matrix A.

Curve Fitting Problems

The application of SVD is used to minimize the least square error. It uses pseudo-inverse for approximation.

Other than this, SVD is also used in digital signal processing and image processing.

Implementation

We will implement the Singular Value Decomposition code in python.

import numpy as np
from scipy.linalg import svd

# define a matrix
X = np.array([[3, 3, 2], [2,3,-2]])
print(X)

# performing SVD
U, sigma, V_transpose = svd(X)

#printing matrices
print("Matrix U: ",U)
print("Sigma matrix: ",sigma)
print("Transpose of V: ",V_transpose)

[[ 3 3 2]
[ 2 3 -2]]
Matrix U: [[ 0.7815437 -0.6238505]
[ 0.6238505 0.7815437]]
Sigma matrix: [5.54801894 2.86696457]
Transpose of V: [[ 0.64749817 0.7599438 0.05684667]
[-0.10759258 0.16501062 -0.9804057 ]
[-0.75443354 0.62869461 0.18860838]]

Image compression using SDV

import numpy as np
from scipy.linalg import svd
import matplotlib.pyplot as plt
from skimage import data
from skimage.color import rgb2gray

astronaut = data.astronaut()

#displating astronaut image
plt.imshow(astronaut)

# converting to grayscale
gray_astronaut = rgb2gray(astronaut)

# calculate the SVD and plot the image
U,S,V_T = svd(gray_astronaut, full_matrices=False)
S = np.diag(S)
fig, ax = plt.subplots(4, 2, figsize=(5, 15))

curr_fig=0
for r in [10, 50, 100, 500]:
ast =U[:, :r] @ S[0:r, :r] @ V_T[:r, :]
ax[curr_fig][0].imshow(256-ast)
ax[curr_fig][0].set_title("k = "+str(r))
ax[curr_fig,0].axis('off')
ax[curr_fig][1].set_title("Original Image")
ax[curr_fig][1].imshow(gray_astronaut)
ax[curr_fig,1].axis('off')
curr_fig +=1
plt.show()

Frequently Asked Questions

What is SVD used for?
Singular Value Decomposition (SVD) is a widely used technique to decompose a matrix into several component matrices, exposing many of the useful and interesting properties of the original matrix.
Does SVD always exists?
Yes, SVD always exists for any square and rectangular matrix.
What is an advantage of SVD?
SVD helps simplify data, removing noise from the data; it is also used for representing the dataset in simple and reduced form.

Key Takeaways

In this article, we have discussed the following topics:

Method to calculate singular value decomposition
Application of SVD
Image compression using SVD

Check out this problem - Matrix Median

Hello readers, here's a perfect course that will guide you to dive deep into Machine learning.

Happy Coding!

Live masterclass

IIT Certification: Key to Success in Data Analytics?

by Coding Ninjas

14 Jan, 2025

01:30 PM

8+ registered

Amazon PowerBI essentials: Data Analyst tips for visualization

by Abhishek Soni, Data Scientist @ Amazon

13 Jan, 2025

01:30 PM

1131+ registered

IIT Certification: Key to Success in Full Stack Development?

by Coding Ninjas

13 Jan, 2025

03:30 PM

392+ registered

IIT Certification: Key to Success in Data Analytics?

by Coding Ninjas

14 Jan, 2025

01:30 PM

8+ registered

Amazon PowerBI essentials: Data Analyst tips for visualization

by Abhishek Soni, Data Scientist @ Amazon

13 Jan, 2025

01:30 PM

1131+ registered

View more events