Singular Value Decomposition and Eigenvalue Decomposition

Eigen Value Decomposition

Eigenvalue decomposition is a form of matrix decomposition. When we wish to calculate a product of matrices equal to the initial matrix, it is known as decomposing a matrix. If we decompose the initial matrix into the product of its eigenvalues and eigenvectors, it is eigenvalue decomposition. Decomposing a matrix regarding eigenvalues and its eigenvectors gives valuable insights into the properties of the matrix. Specific matrix calculations like computing the power of the matrix become much easier when we use the eigendecomposition of the matrix.

Source: Link

Difference between singular value decomposition and eigenvalue decomposition

Let us understand the difference with the help of an example.

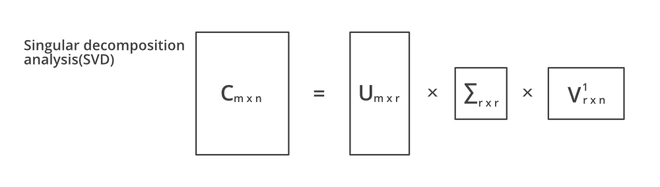
Let's consider the following eigendecomposition A=PDP−1 and SVD A=UΣV* 

The difference between them is:

• In the eigenvalue decomposition matrix P, the vectors are not certainly orthogonal. Therefore, the change of basis isn't a simple rotation. Besides the vectors in the matrices U and V in the SVD are orthonormal, representing rotations (and possibly flips).
• The non-diagonal matrices in Singular value decomposition, i.e., U and V, are not necessarily the inverse of one another. They are generally not related to each other at all. In the eigenvalue decomposition, the non-diagonal matrices P and P-1 are inverse.
• In singular value decomposition, the entries are non-negative and natural in the summation of the diagonal matrix.
• Most of the time, the Singular Value Decomposition exists for any rectangular or square matrix. On the other hand, the eigenvalue decomposition can only exist for square matrices, and even among square matrices, sometimes it doesn't exist.

Mathematics behind singular value decomposition and eigenvalue decomposition

For Eigenvalue decomposition:

Let’s say we’re given a non-defective square matrix A, which has a set of n linearly independent eigenvectors. A can be represented as the diagonal matrix Λ if we express domain and range on the basis of eigenvectors:

A = XΛX^-1

The expression can now be represented in the form Ax= b

b’ = Λx’

Where,

B’ is X^-1b 

X’ is X^-1x

Now, for Singular value decomposition:

As long as we use the correct domain and range spaces, the decomposition of the Singular value generalizes the concept of expressing a matrix as a diagonal matrix to any arbitrary matrix. Having a look at the Ax = b example again, we can now define b based on the left singular vector:

B’ = U*b

And x, i.e., columns of V based on right singular vectors.

X’ = V*x

By solving,

b= Ax⟶U*b = U*Ax =U*U∑V*x⟶b’ = ∑x’

Reducing this,

∑x’ = b’

The mathematical difference between singular value decomposition and eigenvalue decomposition are:

• The eigenvalue decomposition utilizes only the basis, which means the eigenvectors. On the other hand, the singular value decomposition uses two different bases, i.e., left and right singular vectors. 
• In SVD, the eigenbasis is orthonormal, and the basis of eigenvalue decomposition is not orthogonal.
• Every (!) matrix has an SVD; it does not need to be square or fulfil other requirements. On the other hand, not even every square matrix has an eigendecomposition, which is a fundamental difference that makes the SVD very powerful.

Frequently Asked Questions

Is SVD applicable to all matrices?

Unlike the more often used spectral decomposition in Linear Algebra, singular value decomposition is specified for all matrices (rectangular or square). 

Is SVD persistent in all matrices? 

The SVD is always true for every rectangular or square matrix, but the eigendecomposition is only valid for square matrices; it isn't always true among even square matrices. 

Is SVD essential for persistent matrix reduction? 

Significant is the fraction of a vector's linear transformation corresponding to a substantial single value. Positive SVD can be utilized to establish the productive rank of matrix A by counting smaller values as zeros, in addition to what you mention in your query. 

What happens if the eigenvalues are nearly equal?

PCA will not choose the principal components if all eigenvectors are the same because all main features will be similar.

Conclusion

In this article, we have extensively discussed Singular Value Decomposition and EigenValue Decomposition and its difference. We hope that this blog has helped you enhance your knowledge regarding Singular Value Decomposition and EigenValue Decomposition and if you would like to learn more, check out our articles here. Do upvote our blog to help other ninjas grow. Happy Coding!