Sort the matrix

Introduction

In this article, we will discuss the problem of sorting the matrix with examples. The sorted matrix is ​​arranged in such a way that all the elements in a row are sorted in increasing order, and in row 'i', where 1 <= i <= n-1, the first element of row 'i' is greater or equal to the last element of row '1'.

Problem statement

We are given a matrix with sizes of rows and columns. The task is to sort the matrix and in row 'i', where 1 <= i <= n-1, the first element of row 'i' is greater or equal to the last element of row '1'.

Examples

Input 

Rows=2, Coloumns=2, a[2][2] = { {1, 3}, {2, 4} }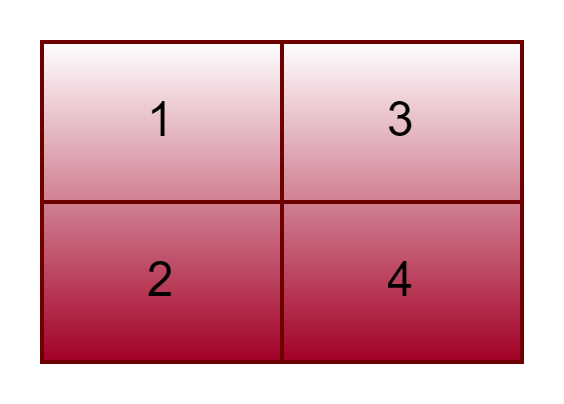

Output

a[2][2] = { {1, 2}, {3, 4} }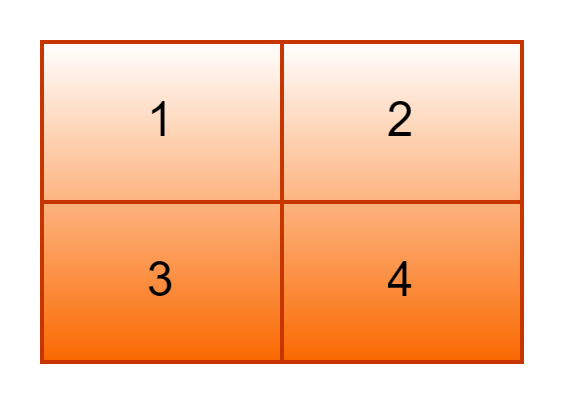

Input 

 Rows=2, Coloumns=3, a[2][3] = { {1, 3}, {2, 4},{5,6} }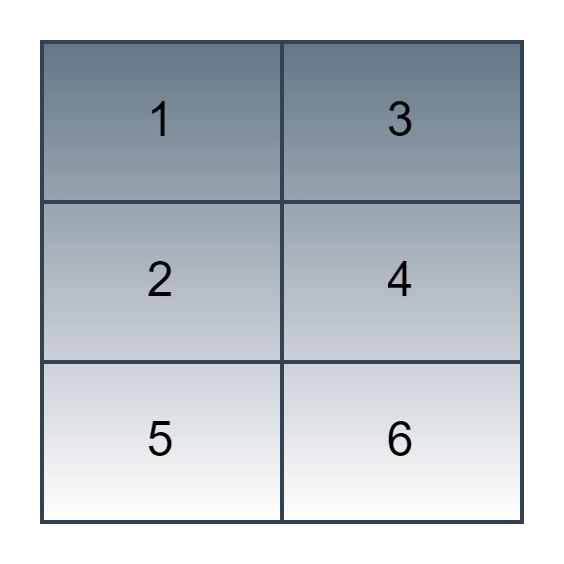

Output 

 a[2][3] = { {1,2}, {3,4},{5,6} }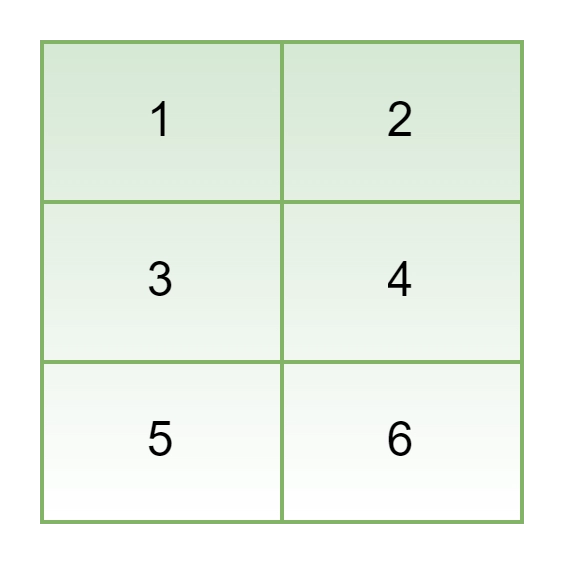

In the above examples, we are sorting the elements of the matrix according to their values. For a detailed explanation running code is shown below.

Approach

The approach to solving this problem is simple and straightforward, firstly we will make a temp array in which the data of the matrix will be stored. Now, we will copy the elements of the matrix into the temp array. Then we will sort that array. After that, we will print the matrix.

Pseudocode

int temp[] = new int[row * col];
int m = 0;
for (int i = 0; i < row; i++)
for (int j = 0; j < col; j++)
temp[m++] = mat[i][j];
Arrays.sort(temp);
m= 0;
for (int i = 0; i < row; i++)
for (int j = 0; j < col; j++)
            mat[i][j] = temp[m++];

Instruction to run the below code

 In case the code is not running directly, then you have to do the following steps:

• Firstly save this code with the name given to the main class.
• Open the terminal and write javac “name of the file”.java to compile the code.
• After compiling it, write java “name of the file” to run the code.

Implementation in Java 

// java program of to sort the matrix.
import java.io.*;
import java.util.*;

public
class matrixsort
{

public
    static void main(String args[])
    {
        int[][] mat = new int[10][10];
        int row, col;
        Scanner sc = new Scanner(System.in);
        System.out.println("Enter the row of the matrix");
        row = sc.nextInt();
        System.out.println("Enter the col of the matrix");
        col = sc.nextInt();
        System.out.println("Enter the element of Matrix");
        // here we are inputting the elements of matrix from user
        for (int i = 0; i < row; i++)
        {
            for (int j = 0; j < col; j++)
            {
                mat[i][j] = sc.nextInt();
            }
        }
        // printing the matrix before sorting using two for loops
        System.out.println("Matrix before sorting");
        for (int i = 0; i < row; i++)
        {
            for (int j = 0; j < col; j++)
                System.out.print(mat[i][j] + " ");
            System.out.println();
        }
        // copying the data of the matrix in the temp array.
        int temp[] = new int[row * col];
        int m = 0;

        for (int i = 0; i < row; i++)
            for (int j = 0; j < col; j++)
                temp[m++] = mat[i][j];
        // after adding the data in temporary array we are using Arrays.sort() function to sort the array
        Arrays.sort(temp);

        m = 0;
        for (int i = 0; i < row; i++)
            for (int j = 0; j < col; j++)
                // filling the data again in matrix from temp array
                mat[i][j] = temp[m++];
        // printing matrix after sorting
        System.out.println("Matrix After Sorting");
        for (int i = 0; i < row; i++)
        {
            for (int j = 0; j < col; j++)
                System.out.print(mat[i][j] + " ");
            System.out.println();
        }
    }
}

You can also try this code with Online Java Compiler

Run Code

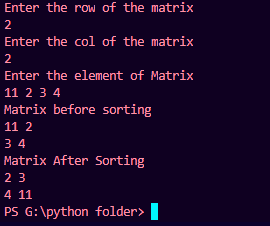
Output

Implementation in C++ 

// c++ program to sort the matrix..
#include <iostream>
#include <algorithm>
using namespace std;

int main()
{
    int row, col;
   
    cout << "\n Enter the size of the row: ";
    cin >> row;
   
    cout << "\n Enter the size of the coloumn: ";
    cin >> col;
    cout << "\n Enter the elements of the matrix: ";
    int mat[row][col];
// here we are inputting the elements of matrix from user
    for (int i = 0; i < row; i++)
    {
        for (int j = 0; j < col; j++)
        {
            cin >> mat[i][j];
        }
    }
// printing the matrix before sorting
    cout << "Matrix before sorting";
    for (int i = 0; i < row; i++)
    {
        for (int j = 0; j < col; j++)
        {
            cout << mat[i][j] << " ";
        }
        cout << endl;
    }
// taking a temp array to store the matrix elements
    int temp[row * col], m = 0;
    for (int i = 0; i < row; i++)
        for (int j = 0; j < col; j++)
            temp[m++] = mat[i][j];

    // sorting the temp[] array 
    sort(temp, temp + m);

    // copy the elements of temp[] one by one
    // in mat[][]
    m = 0;
    for (int i = 0; i < row; i++)
        for (int j = 0; j < col; j++)
            mat[i][j] = temp[m++];

    cout << "Matrix after sorting:"<<endl;
    for (int i = 0; i < row; i++)
    {
        for (int j = 0; j < col; j++)
        {
            cout << mat[i][j] << " ";
        }
        cout << endl;
    }
}

You can also try this code with Online C++ Compiler

Run Code

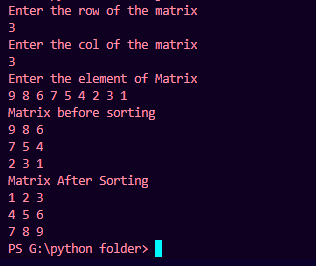
Output     

Complexity analysis

Time complexity

As we all know the time complexity to sort an array of n elements is O(nlogn) but here we have n^2 elements of the matrix, therefore, the time complexity would be O((nlogn)^2), where n refers to the row and column size of the matrix.

Space complexity

O(n) will be the space complexity to store the elements of the sorted matrix.

Also see,  Rabin Karp Algorithm