Introduction
This blog covers a linked list problem. Linked lists are one of the most essential and often asked data structures in programming contests and technical interviews. There are various standard linked list problems and techniques. This blog tackles a coding task that explores how to split a circular linked list into two halves.
Problem Statement
We are given a Circular Linked List of length n. We have to split the circular linked list into two halves. If the given circular linked list has odd numbers of nodes then the first list should contain one extra node.
Sample Examples
Input
Given Circular Linked List:

Output
First List:

Second List:

Explanation
The initial list of 4 nodes is broken into two separate two lists of equal lengths of 2 nodes each.
Input
Given Circular Linked List:

Output
First List:
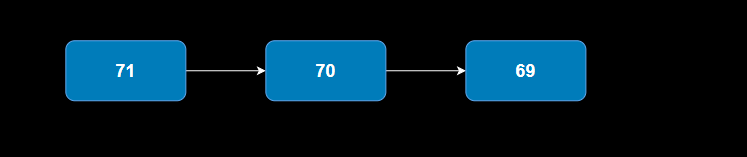
Second List:

Explanation
The initial list of 5 nodes is broken into two separate lists of lengths of 2 and 3 nodes each. If the given Circular linked list has an odd number of nodes the first resultant linked list will have one node more than the second resultant circular linked list.
Recommended Topic, Floyds Algorithm and Rabin Karp Algorithm
Approach
For the given problem, we follow a very interesting approach. We use the slow and fast pointer technique to split the list into two halves by finding the middle node of the list.
After finding the middle node we make the node pointed by the fast pointer the first head and the node pointed by the slow pointer the head of the second half list.
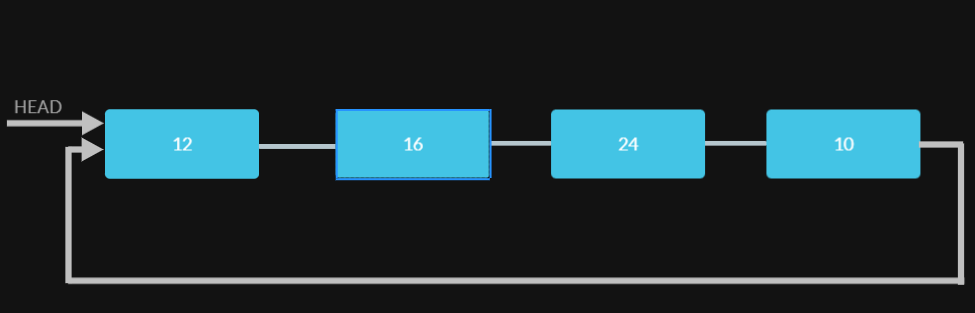
Initial Circular Linked List
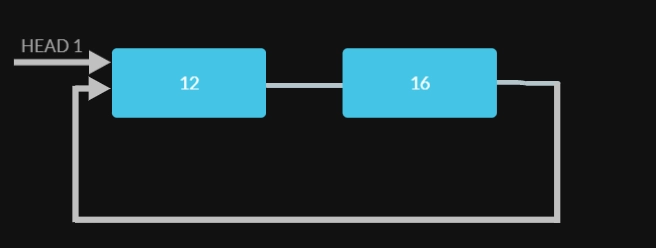
Result Linked List 1
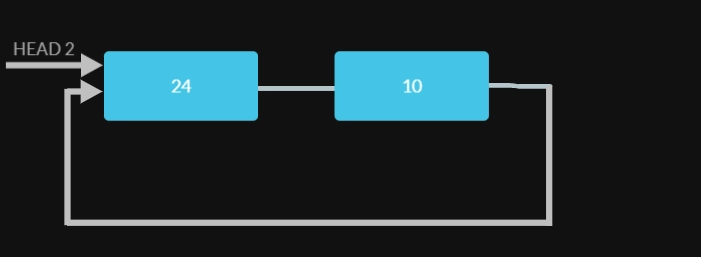
Result Linked List 2
Algorithm
1. Define a circular linked list to be split in half.
2. Create some basic functions, such as creating and displaying a circular liked list.
3. Create a function to divide the list in half.
4. Find the middle of the circular linked list by using the slow and fast pointer trick in this function.
5. When the list is divided in half, there will be two heads.
6. Now, make the node pointed by the fast pointer the first head.
7. The node pointed by the slow pointer will be the second head
8. Finally, display both halves to the user.
Also read - Merge sort in linked list
Implementation
// Program for splitting a circular linked list into two halves
#include <bits/stdc++.h>
using namespace std;
/* Node Structure */
class Node
{
public:
int x;
Node *next;
};
/* Function to split a list (starting with head)
into two lists. */
void listSplitter(Node *head, Node **h1,
Node **h2)
{
Node *slowPtr = head;
Node *fastPtr = head;
if (head == NULL)
return;
/* If there are odd nodes in the circular linked list then
fastPtr->next becomes head and for even nodes
fastPtr->next->next becomes head
as in case of odd number of nodes first list will contain one node
more than second list*/
while (fastPtr->next != head &&
fastPtr->next->next != head)
{
fastPtr = fastPtr->next->next;
slowPtr = slowPtr->next;
}
if (fastPtr->next->next == head)
fastPtr = fastPtr->next;
*h1 = head;
if (head->next != head)
*h2 = slowPtr->next;
fastPtr->next = slowPtr->next;
slowPtr->next = head;
}
/* UTILITY FUNCTIONS */
void pushNode(Node **head, int x)
{
Node *ptr1 = new Node();
Node *temp = *head;
ptr1->x = x;
ptr1->next = *head;
/* If linked list is not equal to NULL then
set the next of last node */
if (*head != NULL)
{
while (temp->next != *head)
temp = temp->next;
temp->next = ptr1;
}
else
ptr1->next = ptr1;
*head = ptr1;
}
/* Function to print nodes in
a given Circular linked list */
void listPrinter(Node *head)
{
string s;
Node *temp = head;
if (head != NULL)
{
cout << endl;
do
{
string p = to_string(temp->x);
s+=p;
s.push_back('-');
s.push_back('>');
temp = temp->next;
} while (temp != head);
}
s.pop_back();
s.pop_back();
cout<<s<<endl;
}
// Driver Code
int main()
{
int listSize, i;
/* Initialize empty linked lists */
Node *head = NULL;
Node *h1 = NULL;
Node *h2 = NULL;
/* Created linked list will be 12->16->24->10 */
pushNode(&head, 12);
pushNode(&head, 16);
pushNode(&head, 24);
pushNode(&head, 10);
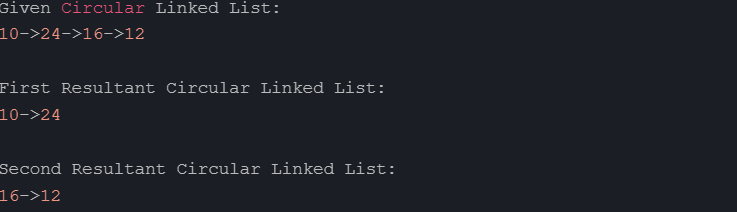
cout << "Given Circular Linked List:";
listPrinter(head);
/* Splitting the list */
listSplitter(head, &h1, &h2);
cout << "\nFirst Resultant Circular Linked List:";
listPrinter(h1);
cout << "\nSecond Resultant Circular Linked List:";
listPrinter(h2);
return 0;
}
Output
Time Complexity
The time complexity of the above approach is O(N), where N is the number of nodes in the linked list.
We have to traverse each node of the linked list to split it into two halves.
Space Complexity
The space complexity of the above approach is O(n).
It's due to the fact that two linked lists of length n/2 are created in this method.




