Introduction
A tree is a data structure in which the elements are stored in hierarchical order. A tree is also defined as a connected acyclic graph or a graph with no cycle. A tree comprises of nodes and edges, where nodes represent the values at that point and edges represent some relation or connection between the nodes.
Problem Statement
Bob is a little boy who loves to play with graphs. His favourite type of graph is a tree. A tree is a connected graph with no cycle. He has defined a new structure which is called a stickman.
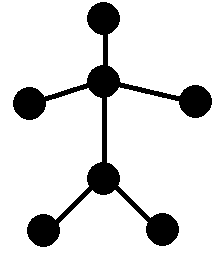
As Bob defined, a stickman is a tree with 7 vertices and 6 edges, in which one vertex must be connected with 4 other vertices and out of these four vertices, one must be connected with two other vertices.
He had a tree of N vertices and counted the number of stickmen in that tree. Two stickmen are distinct if some vertex or some edge is present in exactly one of the two stickmen. The order doesn't matter as long as it fulfils the conditions of the stickman that he defined.
One day a mischievous monkey stole his tree. Now he doesn't remember what his tree looked like. All he remembers is the degree Di of every vertex i of the tree.
Assume that there is a set S of all the random trees with N vertices where the degree of each vertex i is Di. Two trees are distinct if two vertices are connected by an edge in exactly one of the two trees. Now out of all the random trees satisfying the conditions he remembers, help Bob to find the expected number of stickmen in his tree. Find the answer and print it modulo 109 + 7.
Input format
The first line consists of an integer N, the number of vertices in the tree. The following line consists of N integers denoting the degree of each vertex, i.e. D1, D2,..., Dn.
Output format
Print 0 if the expected number of Stickman is 0.
Otherwise, it can be proved that for given constraints, the answer can be uniquely written as a fraction P/Q satisfying conditions:
1) P and Q both are positive integers
2) P and Q are relatively prime (so P/Q is an irreducible fraction)
3) Q is not divisible by 109 +7
Print the value of P * Q-1 modulo 109+7 in a single line.
Constraints
2 <= N <= 105
1 <= Di <= N-1
Note: It is guaranteed that there is at least one tree with the given degrees. So, the described set S isn't empty.
Example
Input
9
4 3 3 1 1 1 1 1 1
Output
428571433
Explanation
As N=9, there are a total of 9 vertices in the tree. The degree of vertices are given 4,3,3,1,1,1,1,1,1. So there are three groups of trees satisfying the conditions.
1)
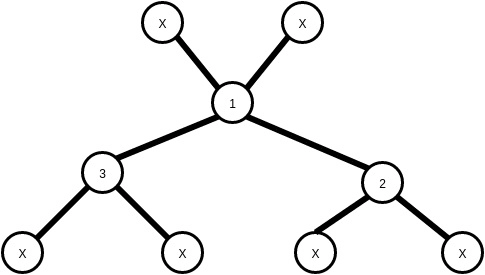
This group of trees has Two stickmen, and there can be 90 such trees. Here X represents any node with degree one. So, a total of 180 stickmen from these 90 trees.
2)
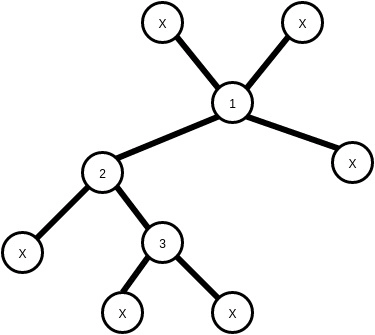
For this group, we have 60 different trees, and each tree has one stickman. So, a total of 60 stickmen from these 60 trees.
3)
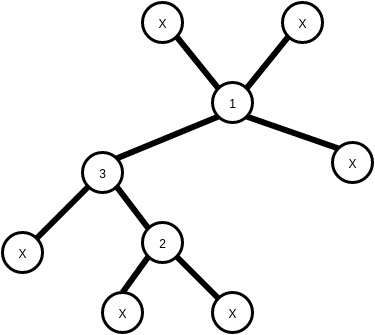
Similarly, for this group, there are 60 such trees, and each tree has one stickman. So a total of 60 stickmen in 60 trees.
Now, the expected number of stickmen is equal to (180 + 60+ 60)/(90+60+60) = 300/210 = 10/7.
So, P is 10, and Q is 7. We need to print the answer in P * Q-1 modulo 109+7.
Here, 7-1 modulo 109 + 7 = 142857144.
Answer = 10 * 142857144 mod (109+7) = 428571433.
Hence, the output is 428571433.
Also see, Euclid GCD Algorithm




