Introduction
One of the most common data structures is the array. An array is a collection of data elements of the same type. There is a very high probability of getting a question related to an array in an interview. So in order to understand the concept of array deeply, we have to practice more and more questions related to the array. In this blog, we are going to discuss a coding problem in which we have to print the count of even-odd subarrays in an array.
Must Recommended Topic, Hash Function in Data Structure.
Problem Statement
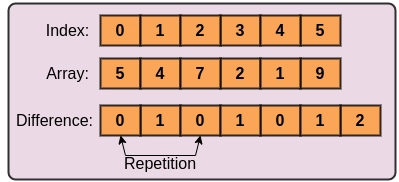
Ninja has given you an array of integers of size N. Your task is to print the count of even-odd subarrays. Here, an even-odd array means an array that contains the same number of even and odd elements.
Sample Examples
Example 1
Input
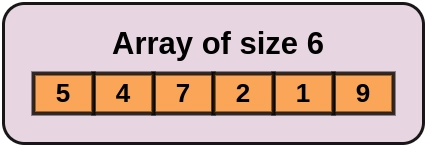
Output
Total Number of even-odd Subarray: 6
Explanation
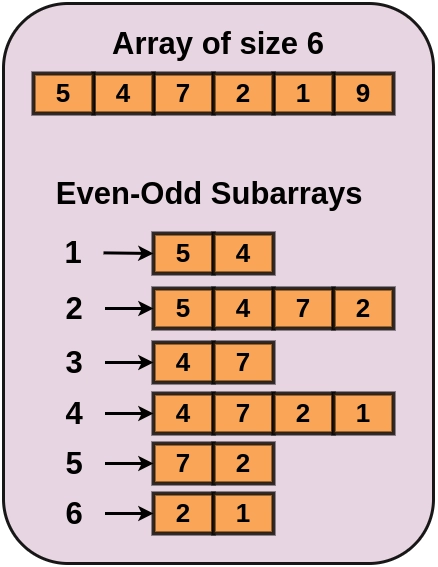
Example 2
Input
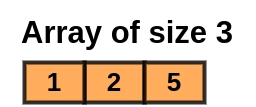
Output
Total Number of even-odd Subarray: 2
Explanation
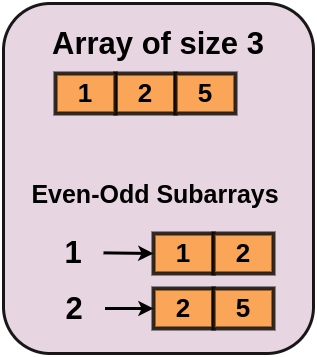
Naive Approach
A simple approach would be to generate all the possible subarrays and check while generating whether the subarray is an even-odd subarray or not.
Algorithm
ALGORITHM(ARR):
totalCount <- 0
for i <- 0 to arr.size():
for j <- i to arr.size():
if subarray from i to j contains equal even and odd elements:
totalCount <- totalCount + 1
end
end
return totalCountImplementation in C++
#include <bits/stdc++.h>
using namespace std;
// function to check if the subarray has equal number
// of even and odd elements
bool checkEvenOdd(vector<int> arr, int i, int j){
// variables to store the count of even and odd elements
int evenCount = 0;
int oddCount = 0;
// looping through the subarray and increasing the even and odd count
for(;i <= j; i++){
if(arr[i] % 2 == 0) evenCount++;
else oddCount++;
}
// The below expresion will return true if evenCount is equal to oddCount
// else it will return false
return evenCount == oddCount;
}
int getCount(vector<int> arr){
// For storing the totalCount of even-odd subarrays
int totalCount = 0;
// generating subarrays and checking whether they contain
// equal amount of even and odd subarray or not.
for( int i = 0; i < arr.size(); i++){
for( int j = i; j < arr.size(); j++){
// checking if the subarray contains equal number of even and odd
// elements
if (checkEvenOdd(arr, i, j)){
totalCount++;
}
}
}
return totalCount;
}
// main method
int main(){
// getting array elements from user
int n; cout << "Enter the size of the array: ";
cin >> n;
vector<int> arr(n);
cout << "Enter array elements: ";
for(int i = 0; i < n; i++) cin >> arr[i];
// getting the count of even-odd subarrays
cout << "Total Number of even-odd Subarray: " << getCount(arr) << endl;
return 0;
}
Input
Enter the size of the array: 6
Enter array elements: 5 4 7 2 1 9
Output
Total Number of even-odd Subarray: 6
Time Complexity
The time complexity of the above code is O(N^3) as we are generating all the possible subarrays. Here, N defines the size of the array.
Space Complexity
Constant space is used. So, the space complexity of the above approach is O(1).
You can also read about the Longest Consecutive Sequence.