Approach
The idea is simple: we search the sublist in the list. If it is present in the list in the same order, we return true, indicating that the sublist is present.
Else, we return false, which means the sublist is not present in the list.
Steps:
-
We have a list_pointer and a sub_pointer pointing to the head of the list and the sublist, respectively.
-
Declare a curr1 pointing to the list_pointer and a curr2 pointer pointing to the sub_pointer.
-
If both the lists are empty, we return true.
-
If the sublist is empty or not empty, and the list is empty, we return false in both cases.
-
After checking for these cases, we start traversing the list while list_pointer!=NULL and point the curr1 pointer to the list_pointer.
-
Now we traverse the sublist while curr2!=NULL, if the curr1 becomes null, we return false else if curr1->data matches with the curr2->data, we move both the pointer to their next node else we break this while loop.
-
After this, if we successfully traversed the whole sublist, i.e. curr2=NULL, it means this sublist is present in the list, and we return true.
-
Else if it is not present, i.e. curr2!=NULL, we point the curr2 pointer again to the starting node of the sublist, i.e. curr2=sub_pointer and move the list pointer to the next node and start searching the sublist again from the list_pointer node.
-
If we successfully traversed the whole list and didn’t get the sublist in it. We return false.
Let’s understand the above steps with example:
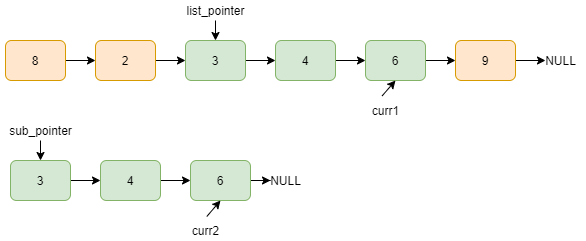
list_pointer and sub_pointer is pointing to the head of the list and sublist, respectively and
curr1=list_pointer, curr2=sub_pointer.
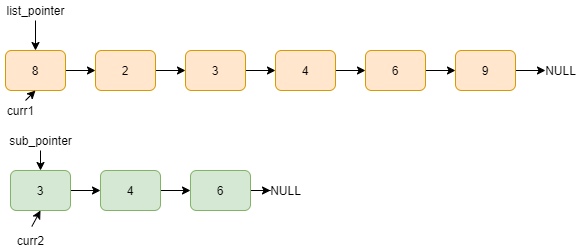
Data of curr1 and curr2 not matches, list_pointer=list_pointer->next, curr1=list_pointer.
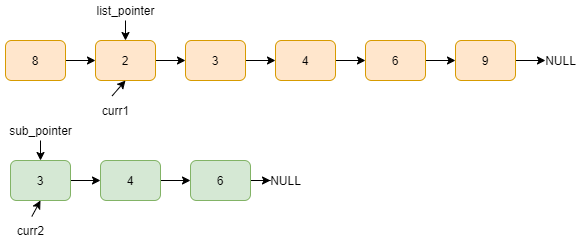
Here, curr1 data and curr2 data matches, curr1=curr1->next, curr2=curr2->next.
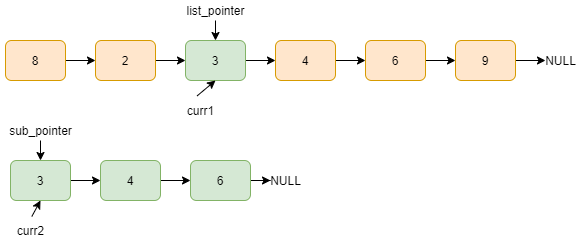
curr1 data and curr2 data matches, curr1=curr1->next, curr2=curr2->next.
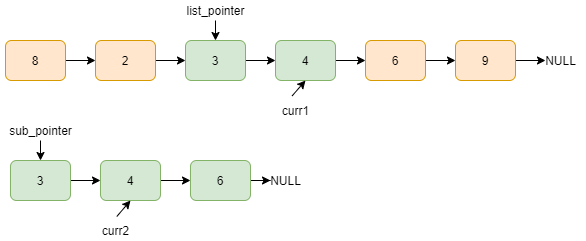
curr1 data and curr2 data matches, curr1=curr1->next, curr2=curr2->next.
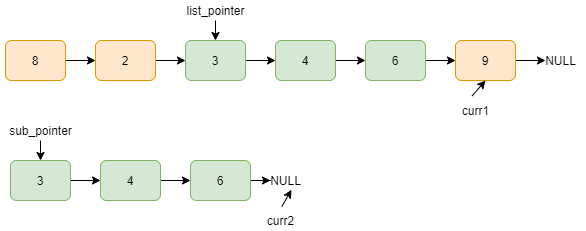
Now, curr2=NULL means we traversed the whole sublist, which indicates that it is present in the list. We return true.
Code in C++
#include <bits/stdc++.h>
using namespace std;
struct Node
{
int data;
Node* next;
Node(int x)
{
data = x;
next = NULL;
}
};
bool isPresent(Node* list_pointer, Node* sub_pointer)
{
Node* curr1 = list_pointer, *curr2 = sub_pointer;
if (list_pointer == NULL && sub_pointer == NULL)
return true;
if ( sub_pointer == NULL || (sub_pointer != NULL && list_pointer == NULL))
return false;
while (list_pointer != NULL)
{
curr1 = list_pointer;
while (curr2 != NULL)
{
if (curr1 == NULL)
return false;
else if (curr2->data == curr1->data)
{
curr2 = curr2->next;
curr1 = curr1->next;
}
else
break;
}
if (curr2 == NULL)
return true;
curr2 = sub_pointer;
list_pointer = list_pointer->next;
}
return false;
}
int main()
{
Node *list = new Node(8);
list->next = new Node(2);
list->next->next = new Node(3);
list->next->next->next = new Node(4);
list->next->next->next->next = new Node(6);
list->next->next->next->next->next = new Node(9);
Node *sub_list = new Node(3);
sub_list->next = new Node(4);
sub_list->next->next = new Node(6);
if (isPresent(list, sub_list))
cout << "true";
else
cout << "false";
return 0;
}

You can also try this code with Online C++ Compiler
Output
true
Complexity Analysis
Time complexity- O(n1*n2), where n1 and n2 are the number of nodes in the first and second linked list, respectively.
Space complexity - The space complexity of the above solution is O(1) as we need constant extra space.
Frequently Asked Questions
What is a linked list?
A linked list is a dynamic data structure in which each element (called a node) consists of two components: data and a reference (or pointer) to the next node. A linked list is a collection of nodes, each of which is linked to the next node by a pointer.
Is a linked list useful?
When you need to do a lot of insertions and removals but not a lot of searching on a list of arbitrary (unknown at compile-time) lengths, linked lists come in handy. It is very efficient to split and join (bidirectionally linked) lists.
Are linked lists quick?
Linked lists are dynamic and have lower insertion/deletion time complexities. However, linked lists require more memory per element in the list and have a slower search time.
Conclusion
So, this article discussed the approach to searching a linked list in another linked list with examples and images for a better understanding and its implementation in C++.
You can learn more about the linked lists and also practice similar problems on Coding Ninjas Studio.
Recommended Problems
Do check out some of the Popular Interview Problems from Top companies like Amazon, Adobe, Google, etc. on Coding Ninjas Studio
Also check out some of the Guided Paths on topics such as Data Structure and Algorithms, Competitive Programming, etc. as well as some Contests, Test Series, Interview Bundles, and some Interview Experiences curated by top Industry Experts only on Coding Ninjas Studio.
In case of any comments or suggestions, feel free to post them in the comments section.















