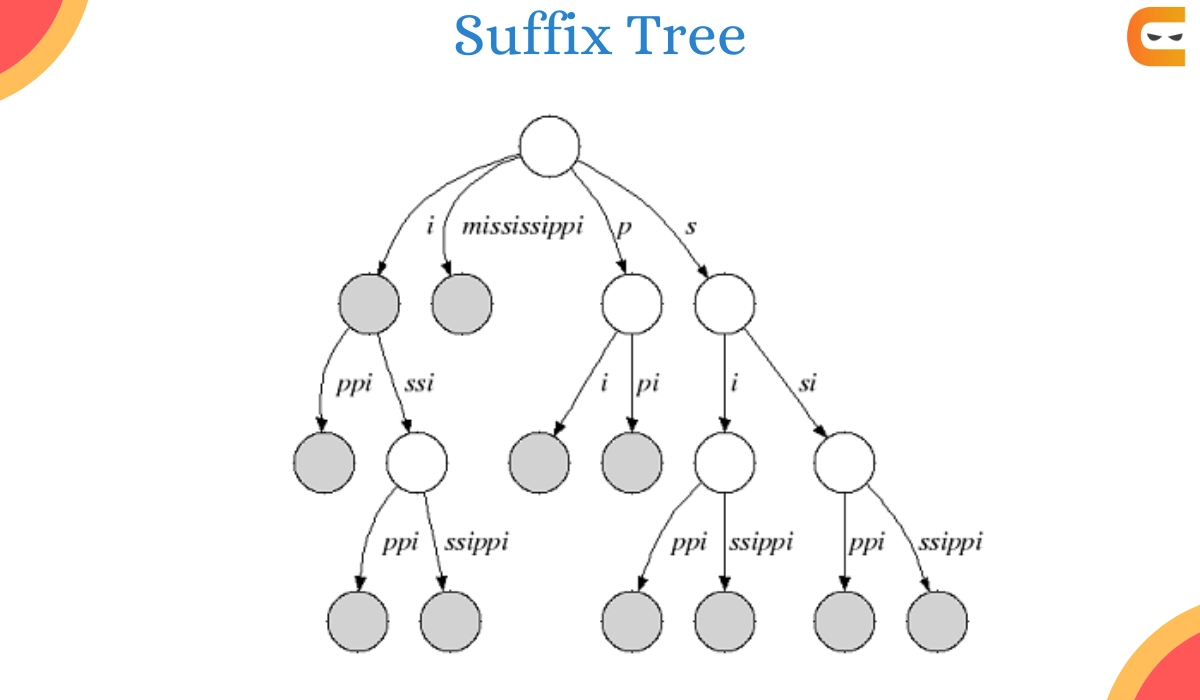
What is a Suffix Tree?🤔
A suffix tree is a compressed trie that stores all of the suffixes in a string. Finding unique substrings in a string, pattern matching, finding the longest palindrome, and other string-related problems have all been proven to be solved efficiently using a suffix tree.
Also, we can check whether a string 'pattern' is contained in another string 'text' or not using a suffix tree. We will generate the Suffix Tree in the following scenario using Ukkonen's Approach, which is a linear time-taking algorithm.
If you want to learn more about Suffix Tree, check out our article on Suffix Tree.
Solution😇
The intuition, approach, and implementation of the above problem are discussed in the following sections.
Intuition
Because we have all of the suffixes stored in a compact fashion in the suffix tree. To find the pattern string, we just need to explore the edges and nodes of the suffix tree. So we'll use two functions to execute this traversal: one to visit the nodes and the other to traverse the edges.
Let’s discuss the approach to solving the problem.
Approach✍️
We will use two functions to traverse the suffix tree: sufNodeTraversal() to tour the nodes, and edgeTraversal() to explore the edges.
⭐ The current edge will be traversed first in function sufNodeTraversal(), with the help of edgeTraversal(), so that the matching substring of the pattern string 'P' and the current part of the suffix can be eliminated, and the remaining part of 'P' can be verified on the child nodes.
⭐ We'll traverse the edge in edgeTraversal() until we reach the end of the pattern string or the current part of the suffix string is finished. While traveling the edge, the following scenarios are possible:
. 💢 If we have reached the end of the pattern string, the answer will be true.
💢 Otherwise, we'll look at the Suffix Tree's later nodes.
Below is the implementation of the above approach.
Implementation💥
/*Program for substring check with the help of Suffix Tree.*/
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int M_CHAR = 256;
string T;
/*Implementation of the Suffix Tree.*/
typedef struct SufTreeNode
{
/*To store the children of the current node.*/
struct SufTreeNode *child[M_CHAR];
/* Pointer to other node via suffix link*/
struct SufTreeNode *sufLink;
int start;
int *end;
/*To store the index of a suffix.*/
int sufIdx;
} sufNode;
/*Root Node.*/
sufNode *root = NULL;
/*Last new node.*/
sufNode *lstNode = NULL;
/*Active node.*/
sufNode *actNode = NULL;
int leafEnd = -1;
int *rootEnd = NULL;
int *splitEnd = NULL;
int actEdge = -1;
int actLength = 0;
int remSufCount = 0;
int len = -1;
sufNode *newNode(int st, int *end)
{
sufNode *node = (sufNode *)malloc(sizeof(sufNode));
for (int i = 0; i < M_CHAR; i++)
node->child[i] = NULL;
node->sufLink = root;
node->start = st;
node->end = end;
node->sufIdx = -1;
return node;
}
int findEdgeLen(sufNode *node)
{
if (node == root)
return 0;
return *(node->end) - (node->start) + 1;
}
int moveDown(sufNode *currNode)
{
if (actLength >= findEdgeLen(currNode))
{
actEdge += findEdgeLen(currNode);
actLength -= findEdgeLen(currNode);
actNode = currNode;
return 1;
}
return 0;
}
void extendSuffixTree(int idx)
{
leafEnd = idx;
remSufCount++;
lstNode = NULL;
while (remSufCount > 0)
{
if (actLength == 0)
actEdge = idx;
if (actNode->child[actEdge] == NULL)
{
actNode->child[actEdge] = newNode(idx, &leafEnd);
if (lstNode != NULL)
{
lstNode->sufLink = actNode;
lstNode = NULL;
}
}
else
{
sufNode *nxt = actNode->child[actEdge];
if (moveDown(nxt))
{
continue;
}
if (T[nxt->start + actLength] == T[idx])
{
if (lstNode != NULL && actNode != root)
{
lstNode->sufLink = actNode;
lstNode = NULL;
}
actLength++;
break;
}
splitEnd = (int *)malloc(sizeof(int));
*splitEnd = nxt->start + actLength - 1;
sufNode *split = newNode(nxt->start, splitEnd);
actNode->child[actEdge] = split;
split->child[0] = newNode(idx, &leafEnd);
nxt->start += actLength;
split->child[actEdge] = nxt;
if (lstNode != NULL)
{
lstNode->sufLink = split;
}
lstNode = split;
}
remSufCount--;
if (actNode == root && actLength > 0)
{
actLength--;
actEdge = idx - remSufCount + 1;
}
else if (actNode != root)
{
actNode = actNode->sufLink;
}
}
}
void setsufIdxByDFS(sufNode *node, int labelHt)
{
if (node == NULL)
return;
int leaf = 1;
for (int i = 0; i < M_CHAR; i++)
{
if (node->child[i] != NULL)
{
leaf = 0;
setsufIdxByDFS(node->child[i], labelHt + findEdgeLen(node->child[i]));
}
}
if (leaf == 1)
{
node->sufIdx = len - labelHt;
}
}
void freeSufTree(sufNode *node)
{
if (node == NULL)
return;
int i;
for (i = 0; i < M_CHAR; i++)
{
if (node->child[i] != NULL)
{
freeSufTree(node->child[i]);
}
}
if (node->sufIdx == -1)
free(node->end);
free(node);
}
void buildSuffixTree()
{
len = T.length();
rootEnd = (int *)malloc(sizeof(int));
*rootEnd = -1;
root = newNode(-1, rootEnd);
actNode = root;
for (int i = 0; i < len; i++)
extendSuffixTree(i);
setsufIdxByDFS(root, 0);
}
int edgeTraversal(string S, int st, int end, int idx)
{
for (int l = st; S[idx] != '\0' && l <= end; idx++, l++)
{
if (T[l] != S[idx])
return -1;
}
if (S[idx] == '\0')
return 1;
return 0;
}
int sufNodeTraversal(sufNode *node, string S, int idx)
{
/*If the given node is null, return -1.*/
if (!node)
return -1;
/*If node has a valid start value.*/
if (node->start != -1)
{
/*Traversing on the parent edge.*/
int tmp = edgeTraversal(S, node->start, *(node->end), idx);
if (tmp != 0)
return tmp;
}
idx = idx + findEdgeLen(node);
/* Now checking for the child nodes.*/
if (node->child[S[idx]] != NULL)
return sufNodeTraversal(node->child[S[idx]], S, idx);
else
return -1;
}
/*Main Function.*/
int main()
{
/*Input of string text and pattern.*/
string P;
cin >> T >> P;
/*Building the Suffix Tree.*/
buildSuffixTree();
int ans = sufNodeTraversal(root, P, 0);
if (ans == 1){
cout << "Yes, the pattern can be found in the text."<<endl;
}
else{
cout << "No, the pattern cannot be found in the text."<<endl;
}
return 0;
}

You can also try this code with Online C++ Compiler
Input
T = “codingninjas” and P = “code”
Output
"No, the pattern cannot be found in the text."
Complexity Analysis🧐
Time Complexity
O(N + M), where N represents the length of the text string T and M represents the length of the pattern string P.
Explanation
Because the Suffix Tree is generated using Ukkonen's Algorithm, it will take O(N) time to complete. Now for the substring check, the traversal is done in the procedures sufNodeTraversal() and edgeTraversal(), which takes a total time of O(M). As a result, the total complexity will be O(N + M).
Auxiliary Space
O(N), where N is the length of the text string T.
Explanation
The Suffix Tree built using Ukkonen's Algorithm takes up O(N^2). Because no extra space is used except for the Suffix Tree, the space complexity will be O(N).
Check out this problem - Longest String Chain
Frequently Asked Questions
What is a tree in data structures?
A tree is non-linear and has a hierarchical data structure consisting of a collection of nodes such that each node of the tree stores a value and a list of references to child nodes.
What is the alternative name of the Suffix tree, and what does it mean?
A suffix tree is also known as a PAT tree or a Position tree in computer science. It's a compressed search tree or prefix tree in which the text location is represented by the suffix of text values in the keys.
How long does it take to build a suffix tree?
The time taken to build a Suffix tree is proportional to its length.
What is the temporal complexity of determining whether or not a string of length n is a substring?
The time complexity of checking if a substring is present in a string of length n is O(n).
Which tree provides a linear time solution for substring operation?
The Suffix tree can provide a linear time solution for substring operations.
Conclusion
In this article, we have extensively discussed checking whether a string 'pattern' is contained in another string 'text' or not using a suffix tree. I hope you enjoyed reading this article on Substring Check using Suffix Tree.
If you want to learn more, check out our articles on Implementing DELETE Method to Delete a User Resource, Technological Services in Ready API, What Is Web2Py?, Why To Use Web2py?, Postbacks and Internationalization in web2py, Third Party Modules In Web2py, Tasks In Web2py, and XML in Web2py.
Recommended problems -
Also, check out these exciting courses from coding ninjas to expand your knowledge, Coding Course, Code Studio, Interview Experience, Guided Path, Interview Problems, Test Series, Library, and Resources.
Happy Coding!