What is a Suffix Tree?
A Suffix Tree is a tree containing all the suffixes of a given string of length n. Suffix Trees help with the fast implementation of long string operations. The positions of each suffix in the text string are recorded as integer indices at the leaves of the Suffix Tree, whereas the path labels (edge labels) of the leaves describe the suffixes.
The i-th suffix of a string T is a substring that goes from the i-th character of the string up to its last character.
For example, if T = "JONATHAN$", then suffix 0 of T is "JONATHAN$", suffix 2 of T is "NATHAN$", suffix 4 of T is "THAN$", etc.
Building and Visualisation
Visualising the Suffix Tree of a string T is a rooted tree where the path label (edge label) from the root to each leaf describes a suffix of T. Each leaf vertex is a suffix, and the value is written inside the leaf vertex is the suffix number. Given below is an example of a suffix tree for the string ABCDE.
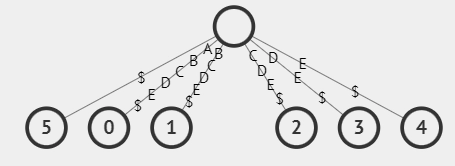
Suffix 0 - ABCDE$
Suffix 1 - BCDE$
Suffix 2 - CDE$
Suffix 3 - DE$
Suffix 4 - E$
Suffix 5 - $
To ensure that every suffix of the input string T ends in a leaf vertex, a special terminating symbol $ is added at the end of the string. This character has an ASCII value lower than the least alphabetical character in T (character 'A' in this visualisation). This is done so that the edge label '$' always appears at the leftmost edge of the root vertex in the Suffix Tree visualisation.
The string ABCDE has distinct characters without repetitions. The suffix tree for strings having repetitive characters has internal nodes in addition to the leaf nodes.
Internal vertices branch out to more than one child vertex. Therefore, there is more than one suffix from the root to the leaves via the internal vertex. The path label of an internal vertex is the prefix that is common among those suffixes.
Here is another example. String S = AAEDDF
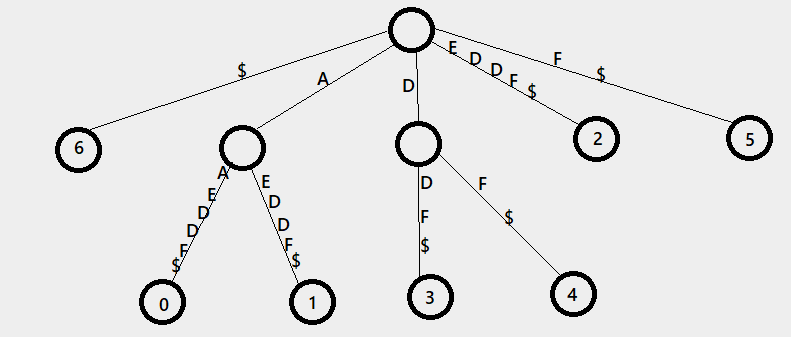
Suffix 0 - AAEDDF$
Suffix 1 - AEDDF$
Suffix 2 - EDDF$
Suffix 3 - DDF$
Suffix 4 - DF$
Suffix 5 - F$
Suffix 6 - $
The characters A and D are repeated twice each. Hence there are two internal nodes. All suffixes end at a leaf vertex, so there are at most n leaves/suffixes in a Suffix Tree. All internal vertices always branch out. Thus, there can be at most n-1 such vertices in cases as shown below.

Thus, the maximum number of vertices in a Suffix Tree is n (leaves) + (n-1) internal vertices = 2n-1 = O(n) vertices. The maximum number of edges in a Suffix Tree is also (2n-1)-1 = O(n) edges.
Also check out - Substr C++
Suffix Tree Approach
Now that we learnt what exactly a Suffix tree is and how to build it, we can use this concept to solve the given problem statement.
The first step is to build a Suffix Tree for the given input string. The next step is to perform a Depth First search over the suffix tree nodes. By doing this, we can find the number of substrings that start at a particular node. As we traverse the tree, keep updating the count of the appearance of substrings.
Frequently Asked Questions
What are the different applications of Suffix Trees in the real world?
Suffix Trees are used in String Matching using various patterns, Computational Biology to find the repetitive patterns in a DNA strand and the longest Palindrome. It is also used in text statistics to find textual factors and in Data compression, where information is encoded with lesser bits than the original representation in signal processing.
What information can be obtained from the suffix tree of a String?
It is possible to find all maximal pairings, maximal repeats, and supramaximal repeats in the string. We can also obtain the longest repeated substrings, the most frequently occurring substrings of minimum length and the shortest substrings that occur only once.
What is the difference between Suffix Trees and Suffix Tries?
Suffix Trees and Tries are very similar. The only difference is that a suffix tree has less "dummy" nodes compared to a suffix trie. Dummy nodes are single characters that increase the lookup operation at the tree. Nodes in a trie have links to shorter context, 'Tree' does not have it. The Suffix Tree for a given text is a compressed trie for all suffixes of the given text.
Conclusion
This article has extensively discussed the solution to The Substrings and Repetitions problem. We briefly discussed the problem statement and moved on to solve the problem using the Suffix Tree approach.
Feeling curious? Coding Ninjas has you covered. Check out our solutions to problems on Suffix Trees and Suffix Arrays. Learn more about the Generalised Suffix Tree and the Brute-force implementation of the Suffix tree. Follow our Guided path for Competitive Programming here.
Recommended problems -
Explore our Library on Coding Ninjas Studio to gain knowledge on Data Structures and Algorithms, Machine Learning, Deep Learning, Cloud Computing and many more! Test your coding skills by solving our test series and participating in the contests hosted on Coding Ninjas Studio!
Looking for questions from tech giants like Amazon, Microsoft, Uber, etc.? Look at the problems, interview experiences, and interview bundle for placement preparations. Upvote our blogs if you find them insightful and engaging! Happy Coding!









