Introduction
We already have an idea that there are many operations that can be performed using a linked list. In this problem, we need to subtract two numbers which are considered linked lists. There are various approaches to solve this problem. So let us dig deeper into this problem statement as well as the solution.
Problem statement
In this problem, we are given two linked lists and are asked to calculate the difference between the linked list and return it. We need to subtract the smaller one from the larger one. To make the smaller one the same length as a larger one, we will append zeroes at the end of it. Suppose we are given two lists L1 and L2. l1 contains 1->2->4->5. This will be considered number 1245. Let L2 be 1->1->1. It will be considered 111. As we can see that L2 is smaller than L1. so we need to subtract L2 from L1. By padding zeroes at the end of L2, it will become 0111. Now we can subtract them. The answer will be 1245-0111=1134. I.e. 1->1->3->4. Let us understand this problem statement with the help of an example.
Sample example
Given two linked lists below. We need to calculate their differences.
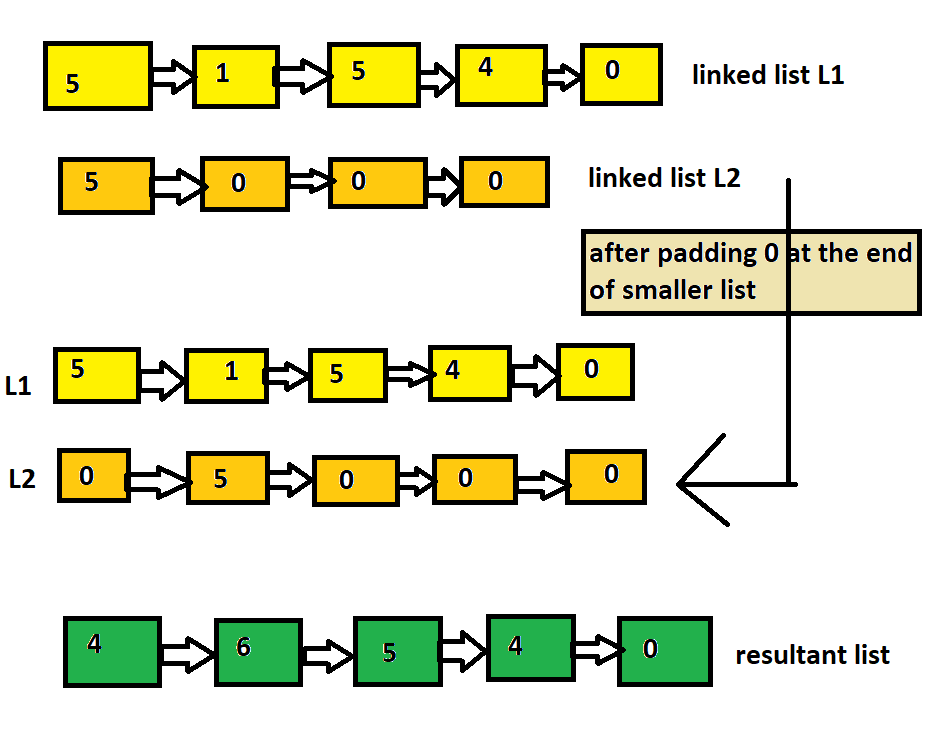
The output is shown in the image itself which is 46540. We simply subtracted the smaller list from the larger one. Now let us see how we did it, its approach, algorithm implementation, and complexities.
Recursive approach
Our strategy will be simple and straightforward. First, we'll check to see if our linked lists are equal. If they are equal, we will proceed with our subtraction function; otherwise, we will pad 0 at the end of the smaller list. We will treat both lists as numbers. Let us now look at the algorithm for the same.
Algorithm
Step 1: Check the size of both the linked list.
Step 2: If the size of one linked list is smaller than another one. Then we will append zero at the end of the smaller one to make it of equal length.
Step 3: If the length of both the lists is the same. Then we will calculate which list is smaller in number.
Step 4: After knowing which is the smaller one, we will subtract the nodes of the smaller linked list from the larger linked list one by one. We also have to keep in mind the borrow while doing the difference calculation.
Let us understand this approach with the help of a diagram.
Dry run
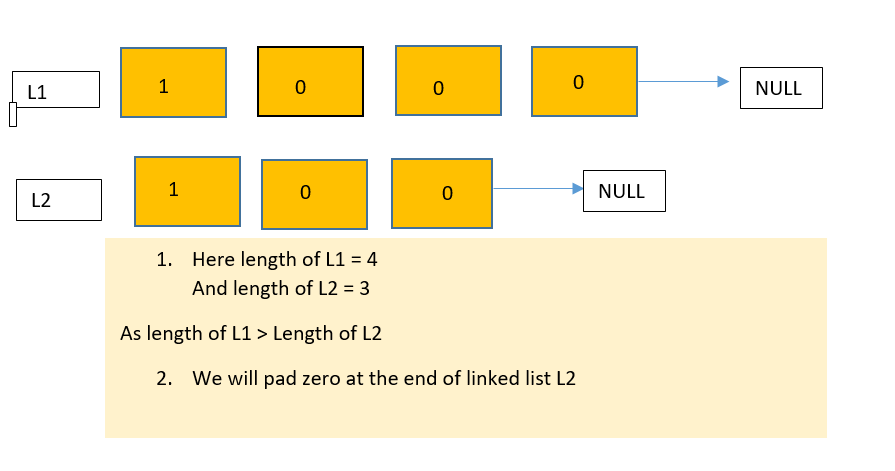
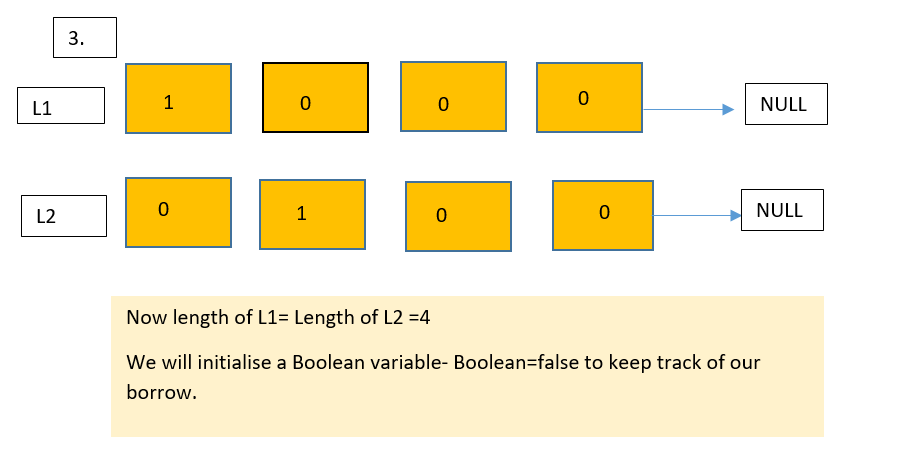
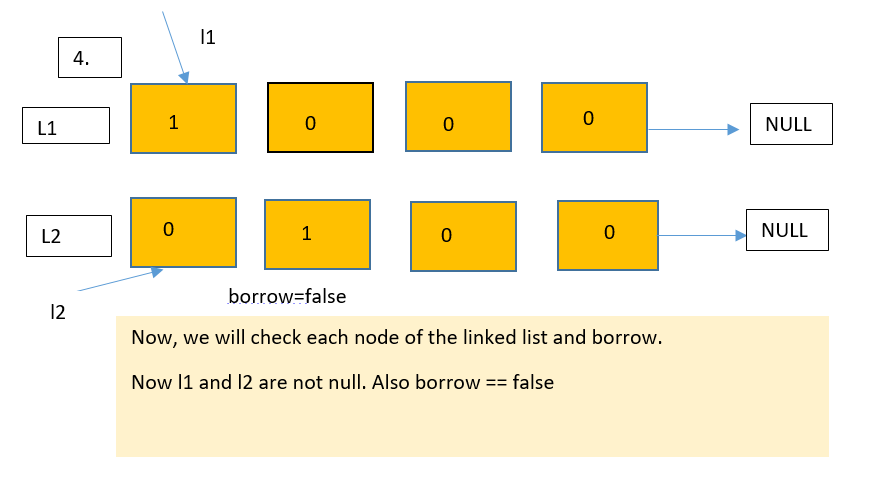
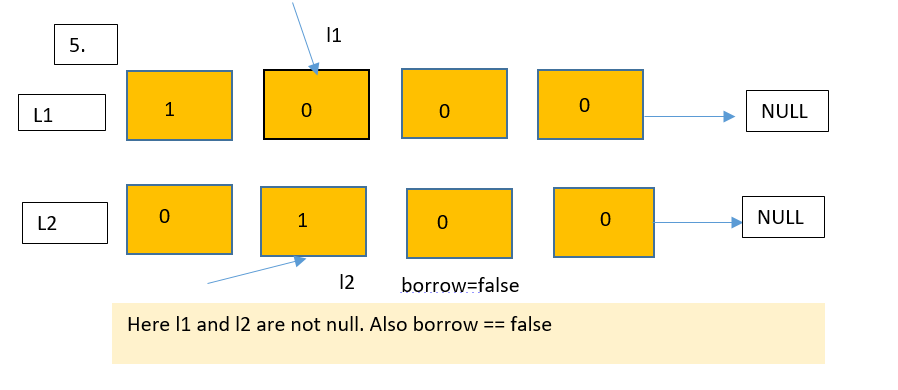
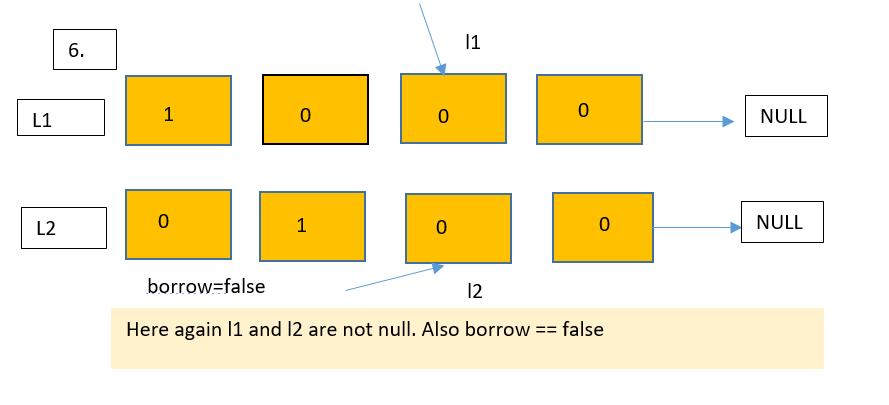
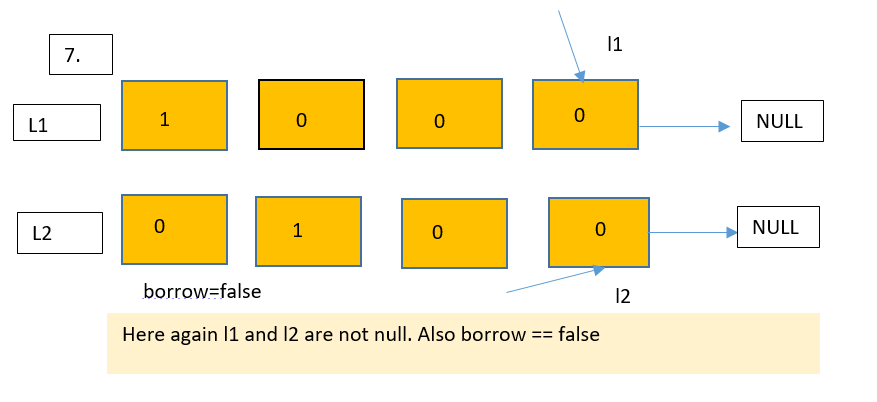
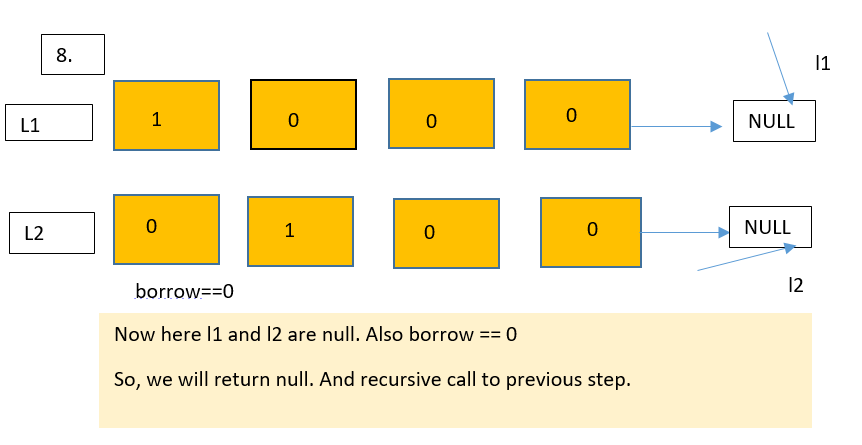
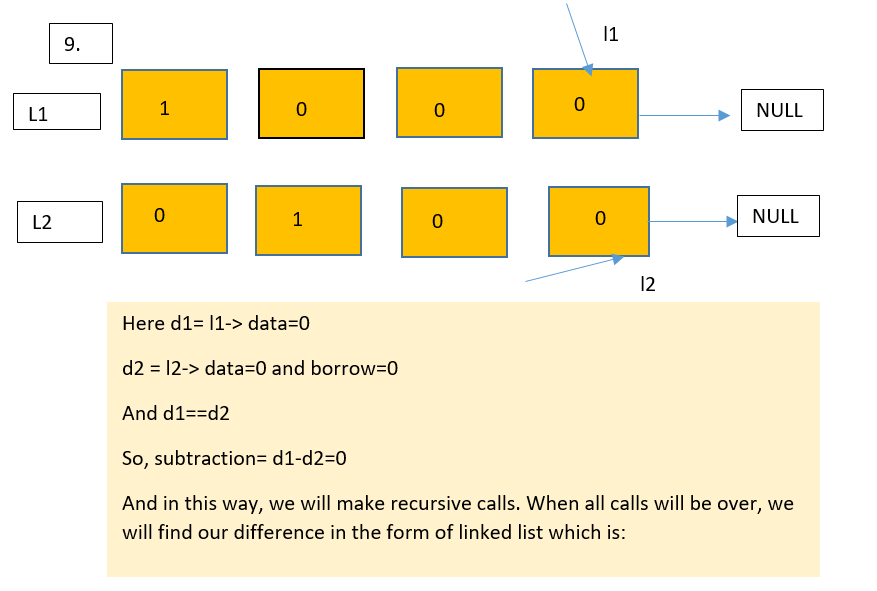
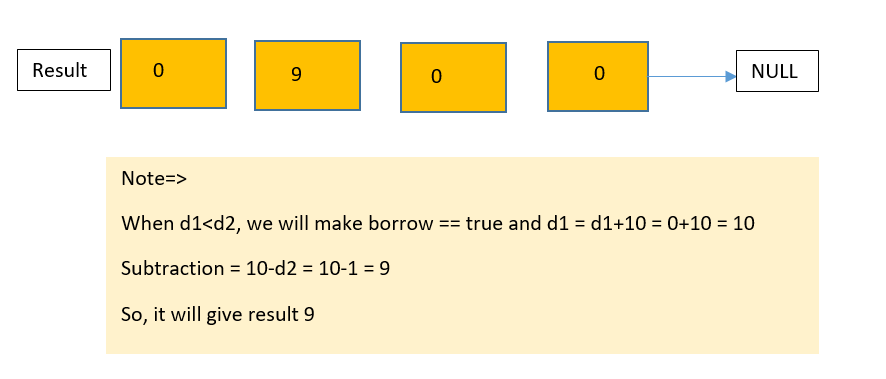
Let us see the implementation of this approach in the next section of this blog.
Implementation in Python
class Node:
def __init__(self, data=None):
self.data = data
self.next = None
# implementation of linked list
class LinkedList:
def __init__(self):
self.head = None
self.length = 0
# Insert a node at the front of the list
def insertNode(self, data):
node = Node(data) # create a node
temp = self.head
self.head = node
self.head.next = temp
self.length += 1 # increment the length
# Insert a node at the end of the list
def insert(self, data):
node = Node(data) # create a node
if self.head == None: # if list is empty insert a node at the start
self.head = node
self.length += 1
else:
temp = self.head
# iterate through the list till last node is found
while temp.next:
temp = temp.next
temp.next = node # adding a new node
self.length += 1
# Return the length of the linked list
def len(self):
return self.length
# print all values of the list
def traverse(self):
temp = self.head
while temp:
print(temp.data, end="\t")
temp = temp.next
print("")
# Add zero at the start of the linked list
def addZero(ll, length):
for i in range(0, length):
zero_node = Node(0)
temp = ll.head
ll.head = zero_node
ll.head.next = temp
return ll
def findSmaller(list_1, list_2):
temp_1 = list_1.head
temp_2 = list_2.head
while temp_1 != None:
if temp_2.data > temp_1.data:
return list_2, list_1
if temp_1.data > temp_2.data:
return list_1, list_2
temp_1 = temp_1.next
temp_2 = temp_2.next
return list_1, list_2
def subtraction(list_1, list_2):
if list_1.len() < list_2.len():
diff = (
list_2.len() - list_1.len()
) # find the number of zeroes to be added at the beginning of the smaller list
list_1 = addZero(list_1, diff)
elif list_2.len() < list_1.len():
diff = list_1.len() - list_2.len()
list_2 = addZero(list_2, diff)
# make list_1 the larger number and list_2 the smaller one
list_1, list_2 = findSmaller(list_1, list_2)
subtractTwoLargeNumber(list_1.head, list_2.head)
borrow = False
result = LinkedList()
# recursive method to find the difference
def subtractTwoLargeNumber(list_1, list_2):
global borrow
global result
if list_1 == None and list_2 == None:
return None
subtractTwoLargeNumber(list_1.next, list_2.next)
if borrow == True:
diff = list_1.data - 1
else:
diff = list_1.data
if diff >= list_2.data:
diff = diff - list_2.data
borrow = False
else:
diff = 10 + diff - list_2.data
borrow = True
result.insertNode(diff) # add difference at the start of the result linked list
ll1 = LinkedList() # create list_1
ll1.insert(1)
ll1.insert(0)
ll1.insert(0)
ll1.insert(0)
ll2 = LinkedList() # create list_2
ll2.insert(1)
ll2.insert(0)
ll2.insert(0)
print("Linked List 1:")
ll1.traverse()
print("Linked List 2:")
ll2.traverse()
subtraction(ll1, ll2)
print("Resultant List:")
result.traverse()Output
Linked List 1:
1 0 0 0
Linked List 2:
1 0 0
Resultant List:
0 9 0 0Implementation in C++
#include <bits/stdc++.h>
using namespace std;
struct Node { //creation of linked list
int data;
struct Node* next;
};
Node* newNode(int data){
Node* temp = new Node;
temp->data = data;
temp->next = NULL;
return temp;
}
int getLength(Node* Node){ //get the length of both the lists
int size = 0;
while (Node != NULL) {
Node = Node->next;
size++;
}
return size;
}
Node* paddZeroes(Node* smallerNode, int diff){ // to add difference in the smaller list
if (smallerNode == NULL)
return NULL;
Node* zHead = newNode(0);
diff--;
Node* temp = zHead;
while (diff--) {
temp->next = newNode(0);
temp = temp->next;
}
temp->next = smallerNode;
return zHead;
}
//recursive functions for the subtraction
Node* subtraction(Node* L1, Node* L2, bool& borrow){
if (L1 == NULL && L2 == NULL && borrow == 0)
return NULL;
Node* previous
= subtraction(
L1 ? L1->next : NULL,
L2 ? L2->next : NULL, borrow);
int d1 = L1->data;
int d2 = L2->data;
int sub = 0;
//if you have given the value to next digit then reduce the d1 by 1
if (borrow) {
d1--;
borrow = false;
}
//If d1 < d2, then borrow the number from previous digit.
//Add 10 to d1 and set borrow = true;
if (d1 < d2) {
borrow = true;
d1 = d1 + 10;
}
//subtract the digits
sub = d1 - d2;
Node* current = newNode(sub);
current->next = previous;
return current;
}
//returns the desired result
Node* subtractLinked(Node* L1, Node* L2){
// Base Case.
if (L1 == NULL && L2 == NULL)
return NULL;
int length1 = getLength(L1);
int length2 = getLength(L2);
Node *largerNode = NULL, *smallerNode = NULL;
Node* temp1 = L1;
Node* temp2 = L2;
if (length1 != length2) {
largerNode = length1 > length2 ? L1 : L2;
smallerNode = length1 > length2 ? L2 : L1;
smallerNode = paddZeroes(smallerNode, abs(length1 - length2));
}
else {
// If both list lengths are equal
while (L1 && L2) {
if (L1->data != L2->data) {
largerNode = L1->data > L2->data ? temp1 : temp2;
smallerNode = L1->data > L2->data ? temp2 : temp1;
break;
}
L1 = L1->next;
L2 = L2->next;
}
}
// If both lNode and sNode still have NULL value,
if(largerNode==NULL&&smallerNode==NULL){
return newNode(0);
}
bool borrow = false;
return subtraction(largerNode, smallerNode, borrow);
}
void printList(struct Node* Node)
{
while (Node != NULL) {
cout<<Node->data;
Node = Node->next;
}
cout<<"endl";
}
int main(){
Node* head1 = newNode(1);
head1->next = newNode(0);
head1->next->next = newNode(0);
head1->next->next->next = newNode(0);
Node* head2 = newNode(1);
head2->next = newNode(0);
head2->next->next =newNode(0);
cout<<"Linked List 1: ";
printList(head1);
cout<<"Linked List 2: ";
printList(head2);
Node* result = subtractLinked(head1, head2);
cout<<"Resultant List is: ";
printList(result);
return 0;
}Output
Linked List 1: 1 0 0 0
Linked List 2: 1 0 0
Resultant List is: 0 9 0 0Let us analyze the time and complexity of this approach.
Complexity analysis
Time complexity
This approach will take O(N), where N is the total number of nodes in the linked list.
Space complexity
In this approach, If recursive stack space is taken into account, it will take O(N).
Also see, Rabin Karp Algorithm





