Suffix Trees (Implementation - Brute Force)

Approach

The idea of creating a suffix tree using the brute force algorithm is to insert each Suffix and compress the resultant trie. Here we squeeze a chain of nodes into a single node; observe the example given below. 

We will keep inserting a node if it doesn't exist. If a relevant node exists, we go through the label of that node and check how much of the current Suffix ([i:n-1]) matches with the label. If we match entirely, we move on to its child; otherwise, we create two new nodes if we partially match. Matched label part is put into a node, the unmatched label node is made its child, and the remaining Suffix string is also made its child. We follow the above process to obtain our entire suffix tree.

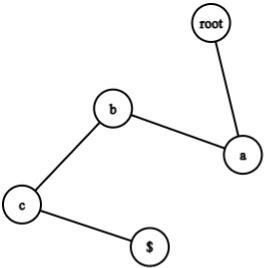
The above chain of nodes converges into the single node below.

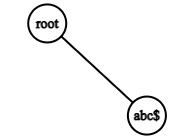
The compressed chain of characters is created to save memory

Steps followed in the code to realise the algorithm.

1. Add an extra character to the end of text S that doesn't exist in S. We added the '$' symbol in our case. We will obtain N separate leaf nodes due to this.
2. Create a root with no label.
3. Insert all N suffixes into the suffix tree (compressed trie of suffixes) one by one.
4. For each Suffix, We insert a node for it doesn't exist.
5. If the node exists, we match the Suffix with its label. If we match entirely, then we move on to the child node.
6. If we only partially match, we create two nodes, assign the matched portion to one node and the suffix string's remaining part to the other, and make the previous node's parent its parent. Make the previous node its child and change its label to the unmatched portion. The other child will be the node with the remaining suffix string node.
7. After doing all the above, we obtain the suffix tree.

Code in Python

class Node:
   """
   Class representing a singular node in a suffix tree
   """
   def __init__(self, set_label):
       self.node_lab = set_label
       self.nexts = {}
class SuffixTreeBruteForce:
   """
   This implementation takes O(M^2) time to build the suffix tree and consumes O(M) Nodes (<= 2 * M - 1)
   """
   def __init__(self, s):
       """
       Build Suffix Tree here
       """
       # add a char that didn't occur earlier in the text like '$' to the end
       s += '$'
       
       # creating root of our suffix tree
       self.root = Node(None)
       
       for i in range(len(s)):
           # insert individual suffixes [i, len(s) - 1]
           curr = self.root
           j = i
           while(j < len(s)):
               if s[j] in curr.nexts:
                   child = curr.nexts[s[j]]
                   label = child.node_lab
                   
                   # check if the current node label is entirely consumed by the suffix
                   k = j
                   label_end = False
                   while(k - j < len(label)):
                       if(k == len(s)):
                           # suffix comes short of the label's length
                           label_end = True
                           break
                       elif(s[k] == label[k-j]):
                           # we keep checking for matching character in suffix with node label
                           k += 1
                       else:
                           # we reached a mismatch in the label
                           # prompting us to make introduce two new nodes
                           label_end = True
                           break
                   
                   if label_end:
                       # special case, here we create two new nodes
                       # we create a node here with the left half of the label (the part that matched) and replace the child node's position with it
                       curr.nexts[s[j]] = Node(label[:k-j])
                       
                       # the new position of the child node is as child of the previosly created node
                       curr.nexts[s[j]].nexts[label[k-j]] = child
                       # it's label is now the right part of label(the unmatched part)
                       child.node_lab = label[k-j:]
                       
                       # we also create another Node containing the unmatched part of the suffix
                       curr.nexts[s[j]].nexts[s[k]] = Node(s[k:])
                       break
                   else:
                       # the whole node was consumed and we move to it's child
                       curr = child
                       j = k
               else:
                   # no child found, create child and end execution
                   curr.nexts[s[j]] = Node(s[j:])
                   break
   
   def findSubstring(self, s):
       """
       function traces through the Suffix Tree for the given string
       and returns true if the string is found, the time complexity for this function is O(len(s))
       """
       curr = self.root
       i = 0
       while(i < len(s)):
           if s[i] in curr.nexts:
               child = curr.nexts[s[i]]
               label = child.node_lab
               
               k = i
               while(k - i < len(label)):
                   if(k == len(s)):
                       # string ends in the middle of label
                       return True
                   elif(s[k] == label[k-i]):
                       # we keep checking for matching character with node label
                       k += 1
                   else:
                       # mismatch
                       return False
               curr = child
               i = k
           else:
               return False
       return True
s = 'auvha jufuvh fuouhkv ovnshdck vhacakd falhvb'
p = SuffixTreeBruteForce(s)
print(p.findSubstring('vha'))
print(p.findSubstring('fuouhkv ovnsdck'))
print(p.findSubstring(' falhvb'))

You can also try this code with Online C++ Compiler

Run Code

Output

True
False
True

Time Complexity

The time complexity of the above algorithm is O(M²) as we insert each Suffix individually into the suffix tree, inserting each Suffix is itself linear.

Space Complexity

The space complexity for this algorithm is O(M²). If our text contains M unique characters, we'll create nodes for each Suffix with label length of Suffix, taking O(M²) memory. This can be easily reduced to O(M) if we store the pair of start index and offset, instead of the whole label (you can try that implementation, you will then observe this method's superiority when compared to Tries, the current algorithm will also generally take lesser space as compared to a Trie).

Frequently Asked Questions

1. What are the advantages of Suffix Tree over Tries?

Suffix Trees consume lesser space, and when you are storing a vast text, the difference between linear and quadratic space complexity can be huge. Suffix tree use can also reduce lookup time.

2. What are the applications of Suffix Tree?

While there are many applications of this data structure, the fundamental ones are searching a string in a Text in O(len(string)) time for multiple checks, searching for longest repeated string, longest common substring, etc. It's also used for searching patterns in DNA or protein sequences.

3. What are the alternatives to Suffix Trees and other possibilities of improvement?

An improvement to the brute force algorithm covered instead of using Suffix Tree is using the Ukkonen's Algorithm (it can construct a suffix tree in O(M) time, the best possible that we can expect). This article here also covers the possibility of replacing suffix trees with enhanced suffix arrays to reduce the space required and solve the same problems with the same time complexity.

Key Takeaways

The article helps us understand the idea behind Suffix Trees, the brute force implementation, improvements and applications. To understand the blog well, read a bit about Tries here and try implementing and understanding the code for a trie before approaching this article.

Learn more about the basics of Python from here if you have trouble understanding some part of the code. Visit the link here for carefully crafted courses on campus placement and interview preparation on coding ninjas.

Happy learning!