Sum of All the Parent Nodes Having Child Node X

Introduction

Data structure and algorithms are one of the most important topics to understand if you want to prepare for a top product-based company. In this article, we will take a quick look at the problem statement and discuss the approach to solve the problem of printing the sum of all the parent nodes having child node X.

In order to find the sum of all the parent nodes having child node x, we will recursively go to each child node of the binary tree in a pre-order fashion and sum up the values of parent nodes. So let’s get started.   

Problem Statement

Ninja has given a binary tree containing n-nodes. Your task is to add up all the parent nodes that have children with the value x.

Sample Examples

Example 1

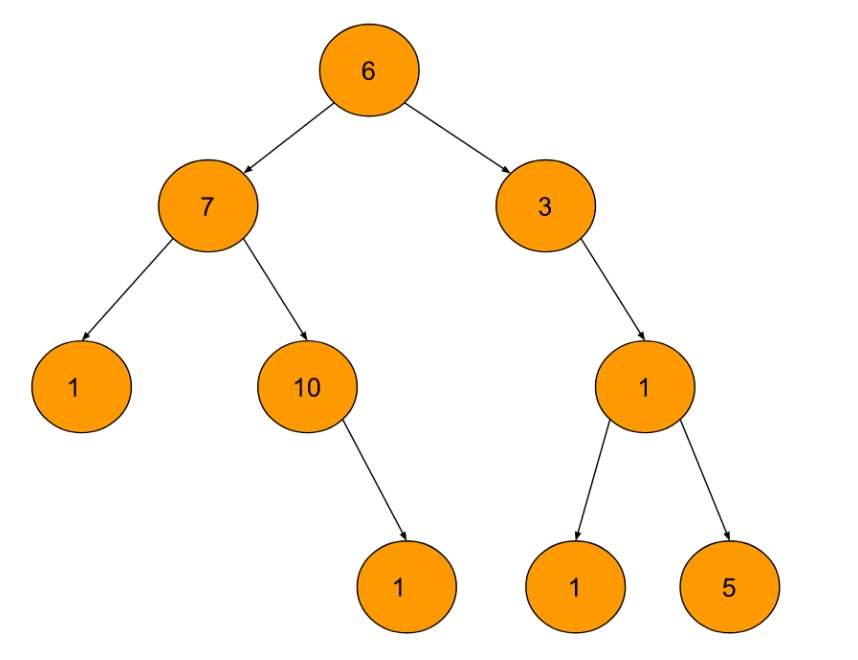
Output

Explanation

In the above example, we can see that {7,3,10,1} are the parents node of the node containing the value ‘1’. The sum of these values is 21.

Example 2

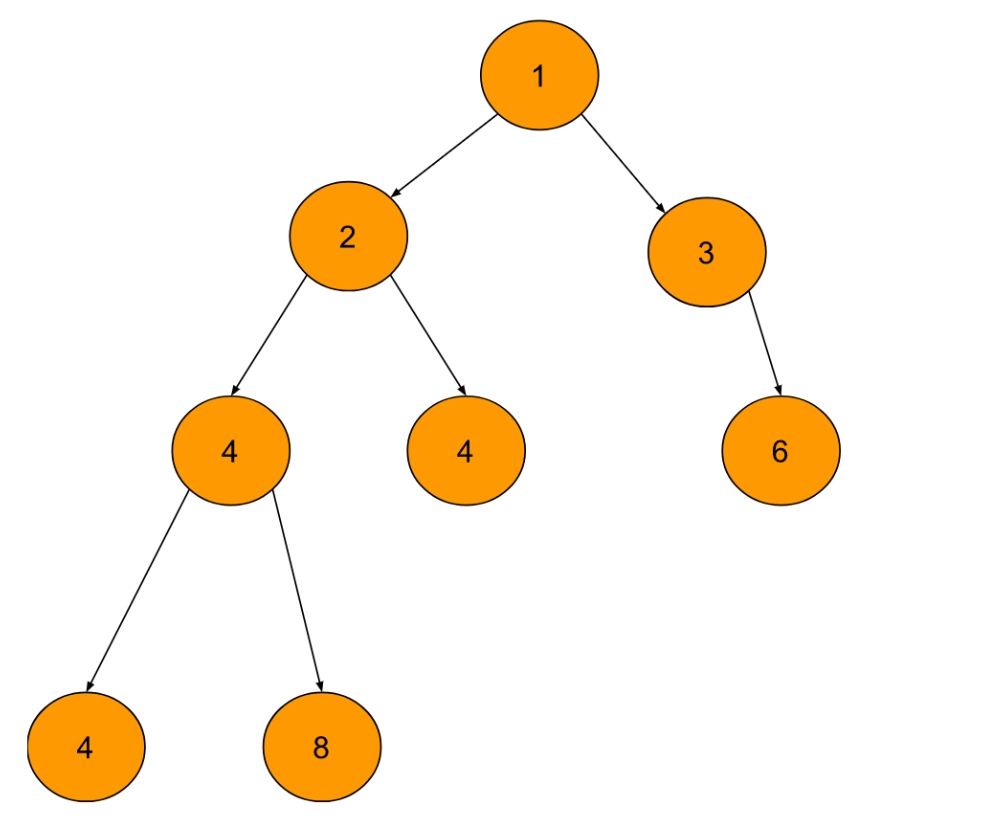
Output

Explanation

In the above example, we can see that {2,2,4} are the parents node of the node containing the value ‘4’. The sum of these values is 8.

Approach (Recursive Solution)

In the problem to find the sum of all the parent nodes having child node x, we are using a recursive- pre-order approach. In this approach, we are recursively going to identify which child node is repeating its value, and then we’ll find who their parents are in a pre-order fashion. Afterward, we will sum up all the parent nodes having the same child nodes. 

Algorithm

1. We will create a binary tree first.
2. Next, we traverse the tree recursively in a pre-order fashion.
3. We will now store all the parent nodes having the same child nodes. 
4. Now we’ll sum up all the parent nodes having the same child nodes.
5. Print the sum now.
6. End

Implementation

#include <iostream>
using namespace std;

//Binary Tree node
class Node
{
    public: int data;
    Node *left;
    Node *right;
    Node(int data)
    {
        //set node value
        this->data = data;
        this->left = NULL;
        this->right = NULL;
    }
};
class BinaryTree
{
    public: Node *root;
    BinaryTree()
    {
        //Set initial tree root to null
        this->root = NULL;
    }
    //Display pre order elements
    void preorder(Node *node)
    {
        if (node != NULL)
        {
            //Print node value
            cout << "  " << node->data;
            this->preorder(node->left);
            this->preorder(node->right);
        }
    }
    // Returns the sum of all parent that child  contains x values
    int parent_sum_of_x(Node *node, int x)
    {
        int sum = 0;
        if (node != NULL)
        {
            if (node->left != NULL && node->left->data == x)
            {
                sum = node->data;
            }
            else if (node->right != NULL && node->right->data == x)
            {
                sum = node->data;
            }
            // Find the x node parent in left and right subtree
            sum = sum + this->parent_sum_of_x(node->left, x) + this->parent_sum_of_x(node->right, x);
        }
        return sum;
    }
};
int main()
{
    //Make object of binary tree
    BinaryTree tree = BinaryTree();
    tree.root = new Node(6);
    tree.root->left = new Node(7);
    tree.root->left->left = new Node(1);
    tree.root->left->right = new Node(10);
    tree.root->left->right->right = new Node(1);
    tree.root->left->right->left = new Node(1);
    tree.root->right = new Node(3);
    tree.root->right->right = new Node(1);
    tree.root->right->right->right = new Node(5);
    tree.root->right->right->left = new Node(1);
    cout << "\n Tree Nodes : ";
    tree.preorder(tree.root);
    int x = 1;
    //Display calculated result
    cout << "\n Sum of parent node of [" << x << "] is : " << tree.parent_sum_of_x(tree.root, x) << "\n";
    return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Output

Time Complexity 

The time complexity of this approach is linear, i.e. O(n). We are using a pre-order approach to traverse and store the elements, that’s why the approach is taking this much time.

Space Complexity

The space complexity of the given approach is O(h) where h is the height of the tree. We are using a pre-order approach to traverse and store the elements, that’s why the auxiliary space required in this approach is O(logn). In the worst case, it would be O(n).