Table of contents

Introduction

Brute Force Approach

2.1.

Algorithm

2.2.

Implementation in C++

2.2.1.

Complexity Analysis

Optimized Approach

3.1.

Algorithm

3.2.

Implementation in C++

3.2.1.

Complexity Analysis

Frequently Asked Questions

4.1.

What is the return type of the sumofSubtree function?

4.2.

What is a Subtree in a binary tree?

4.3.

What are the data members of a TreeNode class?

Conclusion

Last Updated: Jul 4, 2024

Sum of Distance of All Nodes From a Given Node

Author Harsh Goyal

Introduction

This blog will discuss the various approaches to solving the Sum of the distance of all Nodes from a given node problem. Before jumping into the problem to get the Sum of the distance of all Nodes from a given node in a binary tree, let’s first understand what is a binary tree,

A binary tree data structure is a type of tree of data structure in which a node can have at most two children commonly known as the left and right child of the node. Its class has three data members which are as follows:-

Data
Left Node pointer
Right Node pointer

For more information on binary trees, refer to Introduction to Binary Trees.

In this problem, we need to find the sum of the distance of each node from a given node.

For Example:-

Binary Tree:-

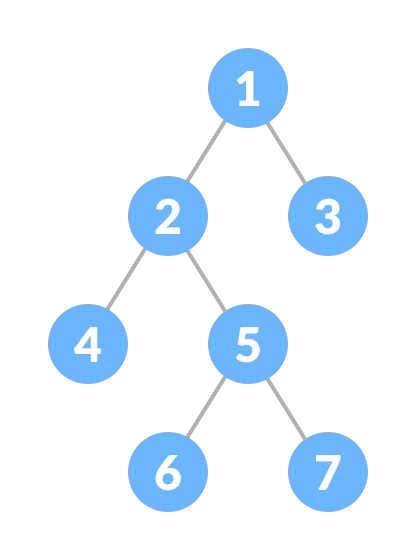
Target Node:- 3

Output:- 14

Brute Force Approach

The brute Force Solution considers calculating the depth and the total number of nodes and then with the help of this information, we need to calculate the sum of the distances of all nodes from a given node.

Algorithm

Step 1. Create a function ‘getResult()’ that will accept four parameters, i.e., one pointer to the root of the binary tree, second will be the target node, third will be the sum of the depth, and fourth will be the number of nodes.

Step 2. Create a function ‘sumofDepth’ to find the sum of all the depths of a node and a variable named ‘sum’ which will denote the sum of the distance of all nodes from the given target node.

Step 3. Now we need to traverse the whole binary tree using DFS Algorithm and for each node, we have to check for that node

If it is the target node given by the user then we need to update the ‘sum’ as the distance

Else,

If the left node of that particular root is not null, then, calculate the total number of nodes in the left subtree and send the value of ‘sum’ as ‘tempsum’.
If the right node of the root is not null, then, calculate the total number of nodes in the right subtree and send the value of ‘sum’ as ‘tempsum’.

Step 4. If we detect the target node, then print the sum of the distances of nodes from that target node.

Implementation in C++

#include <bits/stdc++.h>
using namespace std;

// TreeNode Class
class TreeNode
{
public:
   int data;
  
   // Left Child of the Node
   TreeNode* left;

   //Right Child of the Node
   TreeNode* right;
};

// Add new node to the tree
TreeNode* push(int data)
{
   // Allocate the node
   TreeNode* Node = new TreeNode();

   // Allocate Memory
   Node->data = data;
   Node->left = NULL;
   Node->right = NULL;

   return (Node);
}

// Function to calculate the total sum of depths of all nodes
int depth(TreeNode* root, int x)
{
   // Base Case for this function
   if (root == NULL)
   {
       return 0;
   }

   // Return recursively
   return x + depth(root->left, x + 1) + depth(root->right, x + 1);
}

// Function to count the total number of nodes in the left and right subtree of a given Node
int countNodes(TreeNode* root)
{
   // Base Case
   if (root == NULL)
   {
       return 0;
   }

   // Return recursively
   return countNodes(root->left) + countNodes(root->right) + 1;
}
int sum = 0;

// Function to find sum of distances
// of all nodes from a given node
void getResult(TreeNode* root, int target, int distancesum, int n)
{
   // If target node matches
   // with the current node
   if (root->data == target)
   {
       sum = distancesum;
       return;
   }

   // If left of current node exists
   if (root->left)
   {
       // Count number of nodes in left subtree
       int nodes = countNodes(root->left);

       // Update sum
       int tempsum = distancesum - nodes + (n - nodes);

       // Left Subtreee
       getResult(root->left, target, tempsum, n);
   }

   // If right is not null
   if (root->right)
   {
       // Find number of nodes in right subtree
       int nodes = countNodes(root->right);

       int tempsum = distancesum - nodes + (n - nodes);

       // For right subtree of the node
       getResult(root->right, target,tempsum, n);
   }
}

// Driver Code
int main()
{
   // Input tree
   TreeNode* root = push(1);
   root->left = push(2);
   root->right = push(3);
   root->left->left = push(4);
   root->left->right = push(5);
   root->right->left = push(6);
   root->right->right = push(7);
   root->left->left->left = push(8);
   root->left->left->right = push(9);

   int target = 3;

   // Sum of Depth
   int distanceroot = depth(root, 0);

   // Number of nodes in the left and right subtree
   int totalnodes = countNodes(root);

   getResult(root, target, distanceroot, totalnodes);

   // Print the sum of distances
   cout << "Sum of the distance of all nodes from a given node is:- " << sum << endl;
   return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Output :

Sum of the distance of all nodes from a given node is:- 19

Complexity Analysis

Time Complexity: O(N * N)

Incall to ‘getResult()’, we are traversing the binary tree using DFS and calculating all nodes and the depths, therefore, the overall time complexity is O(N * 2).

Space Complexity: O(N)

As we are using constant extra space, therefore, the overall space complexity will be O(1).

Optimized Approach

To optimize this Sum of the distance of all Nodes from a given node problem, we’ll try to optimize time complexity using one more variable ‘x’, which will denote the count of the total number of nodes present in the left subtree and the right subtree of a particular node. By doing this, we’ll be able to calculate the size of all the subtrees in constant time.

Algorithm

Step 2. Create a function ‘sumofSubtree’ to find the sum of all the depths of a node and a variable named ‘sum’ which will denote the sum of the distance of all nodes from the given target node and it must return the integral pair where the first part will be the number of nodes and the second part will be the depth.

Step 3. Now we need to traverse the whole binary tree using DFS and for each node, we have to check for that node

If it is the target node given by the user, then we need to update the ‘sum’ as distance

Else,

If the left node of that particular root is not null, then calculate the total number of nodes in the left subtree and send the value of ‘sum’ as ‘tempsum’.
If the right node of the root is not null, then, calculate the total number of nodes in the right subtree and send the value of ‘sum’ as ‘tempsum’.

Step 4. If we detect the target node, then print the sum of the distances of nodes from that target node.

Implementation in C++

#include <bits/stdc++.h>
using namespace std;

// TreeNode Class
class TreeNode 
{
public:
   int data, size;
   TreeNode* left;
   TreeNode* right;
};

// Add node to the binary tree
TreeNode* push(int data)
{
   TreeNode* Node = new TreeNode();
   Node->data = data;
   Node->left = NULL;
   Node->right = NULL;

   // Return newly created node
   return (Node);
}

// Function to count the total number of nodes in the left and right subtrees
pair<int, int> sum(TreeNode* root)
{
   // Initialize a pair that stores the pair of number of nodes and depth
   pair<int, int> p = make_pair(1, 0);

   // Count of nodes in the left subtree
   if (root->left)
   {
       pair<int, int> ptemp = sum(root -> left);

       p.second += ptemp.first + ptemp.second;
       p.first += ptemp.first;
   }

   // Count of nodes in the right subtree
   if (root -> right)
   {

       pair<int, int> ptemp = sum(root->right);

       p.second += ptemp.first + ptemp.second;
       p.first += ptemp.first;
   }

   root->size = p.first;
   return p;
}

int ans = 0;

// Function to find the total distance
void getResult(TreeNode* root, int target, int distancesum, int n)
{
   //  If target node given by user matches with the current node
   if (root->data == target)
   {
       ans = distancesum;
   }

   // If root->left is not null
   if (root->left)
   {

       // Update sum
       int tempsum = distancesum - root -> left -> size + (n - root -> left -> size);

       // For the left subtree
       getResult(root -> left, target, tempsum, n);
   }

   // If root->right is not null
   if (root->right)
   {
       int tempsum = distancesum - root->right->size + (n - root -> right -> size);

       // Recursion for the right subtree
       getResult(root->right, target, tempsum, n);
   }
}

// Driver Code
int main()
{
   // Input tree
   TreeNode* root = push(1);
   root->left = push(2);
   root -> right = push(3);
   root -> left -> left = push(4);
   root -> left -> right = push(5);
   root -> right -> left = push(6);
   root -> right -> right = push(7);
   root -> left -> left -> left = push(8);
   root -> left -> left -> right = push(9);

   int target = 3;

   pair<int, int> p = sum(root);

   // Total number of nodes
   int totalnodes = p.first;

   getResult(root, target, p.second, totalnodes);

   // Print the sum of distances
   cout << "Sum of the distance of all nodes from a given node is:- " <<  ans << endl;
   return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Output :

Sum of the distance of all nodes from a given node

Complexity Analysis

Time Complexity: O(N)

Incall to ‘getResult()’, we are calculating the number of nodes in subtree in constant space in the above approach, therefore, the overall time complexity is O(N).

Space Complexity: O(1)

As we are using constant extra space, therefore, the overall space complexity is O(1).

Check out this problem - Pair Sum In Array.

Frequently Asked Questions

What is the return type of the sumofSubtree function?

The return type of the sumofSubtree function is the integral pair. In C++, pair is a type of container which is present in STL, and one can store any kind of data in the form of pair in this.

What is a Subtree in a binary tree?

In a Binary tree, a subtree of a node is recognized as another binary tree whose root node is that particular node. In a Binary tree, there are two types of subtrees

Left Subtree
Right Subtree

Note:- The value of subtree can be Null also.

What are the data members of a TreeNode class?

TreeNode class consists of 3 data members,

Data
Pointer to Left child
Pointer to Right child.

Conclusion

In this article, we discussed the What is Sum of the distance of all Nodes from a given node problem, discussed the various approaches to solving this problem programmatically, the time and space complexities, and how to optimize the approach by reducing the space complexity of the problem.