Introduction
The problem states that we are given a binary tree, and we need to calculate the sum of subtree depths of a given binary tree. Refer to the given sample example to more clearly understand the problem statement.
Binary Tree: As the name suggests, a binary tree is a tree in which every node can have at most two children, and they are known as the left and right children.
Sample Examples
Input: Given The binary Tree
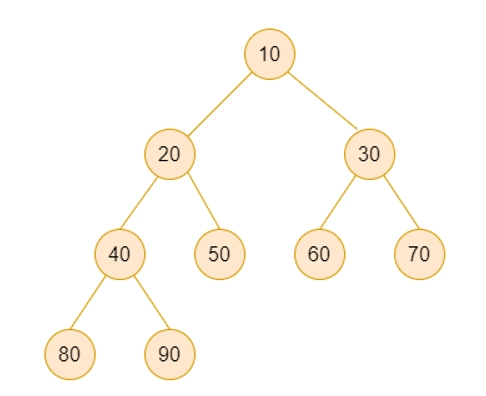
Output: The total sum of subtree depths is: 26.
Explanation:

Let’s denote each subtree of this given binary tree, as 1A, 2A, 2B, 3A.
Let’s Look at each subtree separately, in the given below figure.

Let's denote each subtree of this given binary tree as 1A, 2A, 2B, and 3A.
Let's Look at each subtree separately in the figure given below.
Subtree 3A will have three nodes, 1 node at level 0 and 2 nodes at level 1. So the sum of all depths of subtree 3A will be 1 + 1 = 2.
Subtree 2A will have 5 nodes, 1 node at level 0, 2 nodes at level 1, 2 nodes at level 2. So sum of all depths of subtree 2A will be 1 + 1 + 2 + 2 = 6.
Subtree 2B will have 3 nodes, 1 node at level 0, 2 nodes at level 1, so the sum of all depts of subtree 2B will be 1 + 1 = 2.
Subtree 1A will have 9 nodes, and 1 node at level 0, 2 nodes at level 1, 4 nodes at level 2, 2 nodes at level 3. So sum of all depts of subtree 1A will be 1 + 1 + 2 + 2 + 2 + 2 + 3 + 3 = 16.
So total Sum of subtree depths of given binary tree = 2 + 6 + 2 + 16 = 26.
Now question statement should be clear.
Let's Look at the naive approach to solve the question:
Naive Approach
The idea is simple, traverse every node of the tree, recursively calculate the sum of depths of all nodes for that particular node, and finally print the total sum.
Steps of Algorithm
- Make a function sumOfSubtree() that will calculate the sum of depths of the given root.
- Make another function sumofAllSubtrees() that will call sumOfSubtree for every node, and finally calculate the total sum of all the subtrees.
Implementation in C++
// calulating the sum of subtree depths
#include<bits/stdc++.h>
using namespace std;
class TreeNode{
public:
TreeNode *left, *right;
int data;
TreeNode(int data){
this->left = NULL;
this->right = NULL;
this->data = data;
}
};
int sumOfsubtree(TreeNode *root, int d){
// if there is no node just return 0
if(root == NULL) return 0;
// calulating the sum of the depth of the tree
return d + sumOfsubtree(root->left, d+1) + sumOfsubtree(root->right, d+1);
}
// recursive function to calculate the sum of subtree depths
int sumofAllSubtrees(TreeNode *root){
// if there is no node just return 0
if(root==NULL) return 0;
// calling sum function for current subtree
// calling to left and right tree
return sumOfsubtree(root, 0) + sumofAllSubtrees(root->left) + sumofAllSubtrees(root->right);
}
int main(){
// creating the tree, given in the sample example
TreeNode *root = new TreeNode(10);
root->left = new TreeNode(20);
root->right = new TreeNode(30);
root->left->left = new TreeNode(40);
root->left->right = new TreeNode(50);
root->right->left = new TreeNode(60);
root->right->right = new TreeNode(70);
root->left->left->left = new TreeNode(80);
root->left->left->right = new TreeNode(90);
cout << sumofAllSubtrees(root) << endl;
}
Output:
26
Complexity Analysis
Time Complexity: O(N^2)
Explanation: O(N) for traversing the tree and O(N) for calculating the sum of depths for each node. So total time Complexity is O(N*N).
Space Complexity: O(N)
Explanation: Recursive stack space will be at most O(N).






