Solution Approach
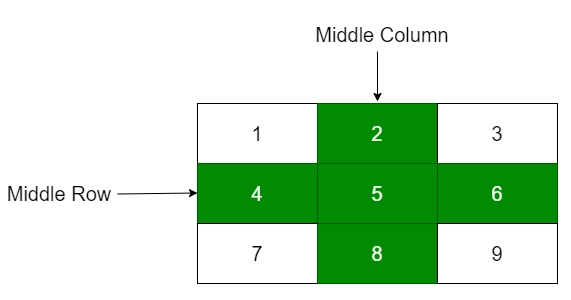
In this approach, we iterate over the matrix's middle row and middle column and sum all the values. The algorithm is as follows:
Step 1: Iterate over the middle row.
Step 2: Sum all the values and print the final value.
Step 3: Iterate over the middle column.
Step 4: Sum all the values and print the final output.
C++ Code
// Program to calculate the sum of the middle row and middle column in a matrix
#include<bits/stdc++.h>
using namespace std;
// function to calculate the sum of the middle row of a matrix
int sumOfMiddleRow(vector<vector<int>> & matrix, int n, int m){
int totalSum =0; //variable to store the total sum value
// Iterating over the middle column and picking the middle value
for(int col = 0; col<m; col++){
totalSum += matrix[n/2][col];
}
return totalSum;
}
// function to calculate the sum of the middle column of a matrix
int sumOfMiddleColumn(vector<vector<int>> & matrix, int n, int m){
int totalSum =0; //variable to store the total sum value
// Iterating over all rows and picking the middle value
for(int row = 0; row<n; row++){
totalSum += matrix[row][m/2];
}
return totalSum;
}
int main(){
int n= 3; // number of rows
int m = 3; // number of columns
// Input
vector<vector<int>> matrix = { {1, 2, 3},
{4, 5, 6},
{7, 8, 9}};
cout<<"Sum of the middle row: "<< sumOfMiddleRow(matrix,n,m)<< endl;
cout<<"Sum of the middle column: "<< sumOfMiddleColumn(matrix,n,m)<< endl;
}
Python Code
#Program to calculate the sum of the middle row and middle column in a matrix
# function to calculate the sum of the middle row of a matrix
def sumOfMiddleRow(matrix, n, m):
totalSum =0 #variable to store the total sum value
# Iterating over the middle column and picking the middle value
for col in range (m):
totalSum += matrix[n//2][col]
return totalSum
# function to calculate the sum of the middle column of a matrix
def sumOfMiddleColumn(matrix, n, m):
totalSum =0 #variable to store the total sum value
# Iterating over all rows and picking the middle value
for row in range (n):
totalSum += matrix[row][m//2]
return totalSum
# function to run the program
if __name__ == "__main__":
n= 3 # number of rows
m = 3 # number of columns
# Input
matrix = [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
print("Sum of the middle row: "+ str(sumOfMiddleRow(matrix,n,m)))
print("Sum of the middle column: "+ str(sumOfMiddleColumn(matrix,n,m)))
Java Code
public class test{
// function to calculate the sum of the middle row of a matrix
public static int sumOfMiddleRow(int [][] matrix, int n, int m){
int totalSum =0; //variable to store the total sum value
// Iterating over the middle column and picking the middle value
for(int col = 0; col<m; col++){
totalSum += matrix[n/2][col];
}
return totalSum;
}
// function to calculate the sum of the middle column of a matrix
public static int sumOfMiddleColumn(int [][] matrix, int n, int m){
int totalSum =0; //variable to store the total sum value
// Iterating over all rows and picking the middle value
for(int row = 0; row<n; row++){
totalSum += matrix[row][m/2];
}
return totalSum;
}
public static void main(String[] args) {
int n= 3; // number of rows
int m = 3; // number of columns
// Input
int [][]matrix = {{1, 2, 3},
{4, 5, 6},
{7, 8, 9}};
System.out.println("Sum of the middle row: " + Integer.toString(sumOfMiddleRow(matrix,n,m)));
System.out.println("Sum of the middle column: "+ Integer.toString(sumOfMiddleColumn(matrix,n,m)));
}
}
Output
Sum of the middle row: 15
Sum of the middle column: 15
The Time complexity of this solution is O(N+M), where N is the number of rows and M is the number of columns.
Frequently Asked Questions
What is the space complexity of the above approach?
Because we are only using a unit amount of extra space, the space complexity of the above approach is O(1). This unit space is used to store the variables: totalSum, n, m etc.
Can the above problem be solved with a time complexity less than O(N + M)?
As we are iterating over the matrix's middle row and middle column and they contain n+m elements. Therefore the time complexity of the above approach can not be improved further.
What is the advantage of utilising a vector rather than an array in CPP?
A vector is a type of dynamic array. Its size can be increased, but the array's size cannot. Vector provides much more flexibility than the array. Therefore, it's preferred.
Conclusion
In this article, we have extensively discussed the problem of calculating the sum of the middle row and column in a matrix. We hope that this blog has helped you enhance your knowledge, to learn more, check out this article.
Recommended Readings:
And also, check out the awesome content on the Coding Ninjas Website,
Android Development, Coding Ninjas Studio Problems, Coding Ninjas Studio Interview Bundle, Coding Ninjas Studio Interview Experiences, Coding Ninjas Courses, Coding Ninjas Studio Contests, and Coding Ninjas Studio Test Series. Do upvote our blog to help other ninjas grow. Happy Coding!