Table of contents

Problem

1.1.

Example 1

1.2.

Example 2

Naive Approach

2.1.

Implementation

2.2.

Time Complexity

2.3.

Space Complexity

Efficient Approach

3.1.

Implementation

3.2.

Time Complexity

3.3.

Space Complexity

FAQs

Key Takeaways

Last Updated: Mar 27, 2024

Sum Of The Values Of All Paths In A Grid

Author Jaglike Makkar

Problem

You are given two integers N and M, representing the dimensions of a grid. There are K special cells in the grid. Each special cell has some value associated with it. A special cell is represented by Xi, Yi, Vi, describing the (x,y) coordinates of the cell and the value V. Your task is to find the sum of the values of all paths starting from (1, 1) to (N, M) and travelling only right or down to a neighbouring cell.

Example 1

Input:

N = 2, M = 3, K = 2

X1 = 1, Y1 = 2, V1 = 1

X1 = 2, Y1 = 3, V1 = 1

Output: 5

Explanation:

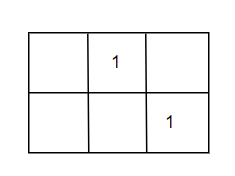
The above image represents the grid. There are total 3 paths from (1, 1) to (2, 3):

(1, 1) -> (1, 2) -> (1, 3) -> (2, 3). The sum of the values of all the cells in this path is 1 + 1 = 2.
(1, 1) -> (1, 2) -> (2, 2) -> (2, 3). The sum of the values of all the cells in this path is 1 + 1 = 2.
(1, 1) -> (2, 1) -> (2, 2) -> (2, 3). The sum of the values of all the cells in this path is 1.

Therefore, the sum of the values of all paths is 2 + 2 + 1 = 5.

Example 2

Input:

N = 3, M = 3, K = 2

X1 = 1, Y1 = 2, V1 = 2

X1 = 2, Y1 = 2, V1 = 1

Output: 10

Explanation: The sum of the values of all paths in the above grid is 9.

Naive Approach

We will try to find the contribution of every cell to the sum of the values of all paths in the grid. For example, for a cell with coordinates (i, j), we need to calculate the number of paths from (1, 1) to (N, M) in which this cell appears. Then, its contribution to the answer will be the number of paths * value of (i, j). We can do this for every (i, j) to get the sum of the values of all paths in the grid.

Any path that passes through (i, j) can be broken down into two paths:

(1, 1) -> (i, j) and (i, j) -> (N, M).

Let K1 be the number of ways to reach (i, j) from (1, 1) and K2 be the number of ways to reach (N, M) from (i, j). The total number of paths from (1, 1) to (N, M) that pass through (i, j) will be K1 * K2.

We can calculate the values of K1 and K2 using dynamic programming. Let DP[i][j] be the number of paths from (1, 1) to (i, j). For any cell (i, j), we can reach it either from (i-1, j) or from (i, j-1). So, DP[i][j] = DP[i-1][j] + DP[i][j-1].

Implementation

#include "bits/stdc++.h"
using namespace std;

// Function to find the sum of the values of all paths
void solve(int n, int m, int k, vector<vector<int>> pts){

   // Dp[i][j] = number of ways to reach i,j
   int dp[n][m];
   memset(dp, 0, sizeof(dp));
   dp[0][0]=1;
   
   for(int i=0; i<n; i++){
      for (int j=0; j<m; j++){

         // Calculating dp[i][j] = dp[i-1][j] + dp[i][j-1]
         if (i!=0) dp[i][j] += dp[i-1][j];
         if (j!=0) dp[i][j] += dp[i][j-1];
      }
   }

   // Initialising answer
   int ans = 0;
   for (int i=0; i<k; i++){
      int x = pts[i][0]-1, y = pts[i][1]-1, v = pts[i][2];

      // K1 = no. of paths from (1, 1) to (i, j)
      int k1 = dp[x][y];

      // K2 = no. of paths from (i, j) to (1, 1)
      int k2 = dp[n-x-1][m-y-1];

      // ans = value * k1 * k2
      ans += k1 * k2 * v;
   }

   // Printing the sum of the values of all paths.
   cout<<ans<<endl;
}

// Driver Code
int main(){
   int n = 3, m = 3, k = 2;
   vector<vector<int>> pts = {{1, 2, 2}, {2, 2, 1}};
   solve(n, m, k, pts);
   return 0;
}

Output

Time Complexity

We have iterated over N and M to calculate the DP matrix, so its time complexity will be O(N * M). Then, we iterated over K and calculated the contribution of each point to the final sum of the values of all paths in O(1). So the total time taken will be O(N * M + K). Since K will always be less than N * M, we can write the time complexity as O(N * M).

Space Complexity

We have used a DP matrix to calculate the number of paths from (1, 1) to (i, j), so the space complexity is O(N * M).

Efficient Approach

In the previous approach, the most time-consuming step was to calculate the number of paths from (1, 1) to (N, M). This took O(N * M) time complexity. We will now try to find the number of paths efficiently.

We can use the permutations and combinations to calculate the number of paths from (1, 1) to (i, j). To reach a cell (i, j), we must have visited (i - 1) cells vertically and (j - 1) cells horizontally. Total number of cells that we can visit is (i - 1) + (j - 1). Therefore the formula will be nCr(i + j - 2, i - 1) or we can write it as:
factorial(i + j - 2) / (factorial(i-1) * factorial(j-1)).

Implementation

#include "bits/stdc++.h"
using namespace std;
#define MOD 1000000007
#define ll long long

ll fact[100003];
ll inv[100003];

void fact0()
{
   ll i,j;
   fact[0]=1;
   for(i=1;i<=100000;i++)
   {
      fact[i]=i*fact[i-1]%MOD;
   }
   inv[0]=1;
   inv[1]=1;
   ll p=MOD;
   for (i=2; i<=100000; i++)
      inv[i] = (p - (p/i) * inv[p%i] % p) % p;
   
   for(i=2;i<=100000;i++)
   {
      inv[i]*=inv[i-1];
      inv[i]%=MOD;
   }
}


// Function to find the sum of the values of all paths
void solve(ll n, ll m, ll k, vector<vector<ll>> pts){

   // Initialising answer
   ll ans = 0;
   for (ll i=0; i<k; i++){
      ll x = pts[i][0]-1, y = pts[i][1]-1, v = pts[i][2];

      // K1 = no. of paths from (1, 1) to (i, j)
      ll k1 = fact[x+y]*((inv[x]*inv[y])%MOD);
      k1 %= MOD;

      // K2 = no. of paths from (i, j) to (1, 1)
      ll k2 = fact[n+m-x-y-2]*((inv[n-x-1] * inv[m-y-1])%MOD);
      k2 %= MOD;

      // ans = value * k1 * k2
      ans += (k1 * k2)%MOD * v;
      ans %= MOD;
   }

   // Printing the sum of the values of all paths.
   cout<<ans<<endl;
}

// Driver Code
int main(){
   fact0();
   ll n = 3, m = 3, k = 2;
   vector<vector<ll>> pts = {{1, 2, 2}, {2, 2, 1}};
   solve(n, m, k, pts);
   return 0;
}

Time Complexity

For each special cell, we calculated its contribution to the sum of the values of all paths in O(1) using factorial and inverse factorial. There are total K special cells, so calculating the sum will take O(K) time. Moreover, we precomputed factorial and inverse factorial. This will take O(N + M) time. So, the time complexity is O(N + M + K).

Space Complexity

We have used fact and inv arrays to calculate each special cell's contribution. These arrays can have a maximum size of N + M. Therefore, the space complexity is O(N + M).

Also see, Rabin Karp Algorithm

FAQs

How to calculate the number of paths in a grid from (1, 1) to (N, M) by moving only right or down?
To calculate the number of paths from (1, 1) to (N, M), we can use the Dynamic Programming approach. Dp[i][j] will store the number of paths from (1, 1) to (i, j). The recurrence relation, in this case, will be:
Dp[i][j] = Dp[i-1][j] + Dp[i][j-1]
Thus, we can compute this in O(N * M).
How to calculate nCr % P efficiently?
We can use the factorial method to calculate the value of nCr efficiently. Fact[i] will store the factorial of i mod P. Inv[i] will store the inverse factorial of i mod P. So, our final answer will be Fact[n] * Inv[r] * Inv[n - r]. Fact and Inv arrays can be computed in O(N).

Key Takeaways

In this article, we have discussed finding the sum of the values of all paths in a grid. We first saw the dynamic programming approach, which took O(N*M), and later optimised our code to compute it in O(N + M). We also saw the implementation of both approaches in C++.

Recommended Problems:

We hope that this blog has helped you enhance your knowledge and if you would like to learn more, check out our articles on Coding Ninjas Studio. Do upvote our blog to help other ninjas grow. Happy Coding!