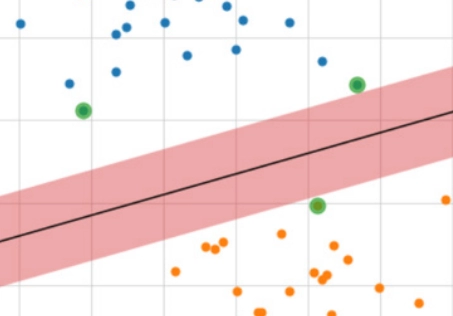
Support Vector Machines Algorithm

Introduction

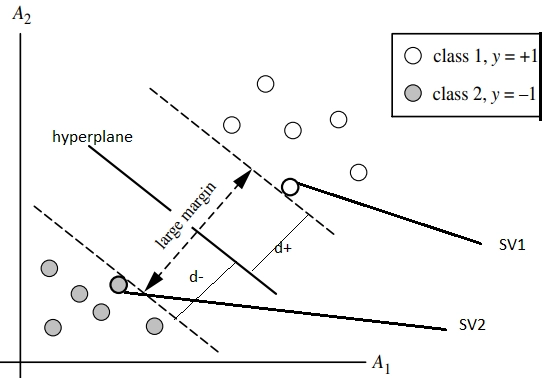
Classification is a fundamental concept in machine learning, used to categorize data into predefined classes. Examples include detecting diseases, identifying spam emails, and detecting fraudulent transactions. Various algorithms solve classification problems, and one of the most effective is the Support Vector Machine (SVM) algorithm. SVM is a powerful machine learning algorithm that finds an optimal hyperplane with the largest margin to separate two classes of data. Similar to Logistic Regression, SVM is widely used for classification tasks.

Let’s explore how SVM works, its key concepts, and practical applications.

Support Vector Machine (SVM)

Support Vectors are the data points that are very close to the hyperplane margin. Or we can also say that, For any hyperplane, support vectors are the data points that define the hyperplane margin. For Example:

source

In the above example, we can say that the green-colored highlighted points are considered to support vectors.
The objective of SVM is to perform a classification task using a liner indicator function i.e., a hyperplane whose margin is as large as possible.

Example:

SVMs can be used for both classification tasks and regression tasks. Let’s solely focus on classification tasks and understand how they work.
In the case of classification tasks, two types of datasets will be present. They are 1. Linearly separable dataset. 2. Linearly Inseparable dataset.

Types of Support Vector Machine

Support Vector Machines (SVMs) are supervised learning models used for classification and regression analysis. There are two main types of SVMs:

Linear SVM: Used for linearly separable data, where a single hyperplane can separate the data into different classes.
Non-linear SVM: Used for non-linearly separable data, where kernel functions transform the data into a higher-dimensional space where it becomes linearly separable.

How does Support Vector Machine (SVM) work?

SVM works by finding the optimal hyperplane that best separates the data points of different classes. The optimal hyperplane is the one that maximizes the margin between the two classes. Here’s a step-by-step explanation:

Identify Support Vectors: The closest data points to the hyperplane, which are critical in defining the position and orientation of the hyperplane.
Maximize the Margin: The distance between the hyperplane and the nearest support vectors is maximized to ensure a robust separation.
Define the Hyperplane: For linear SVM, the hyperplane is defined as a line in 2D or a plane in higher dimensions. For non-linear SVM, kernel functions are used to transform the data into a higher-dimensional space where a linear separation is possible.

Diagram of SVM Working

Linear SVM

Imagine a two-dimensional space where we have two classes of data points: circles and squares.

1. Data Points and Initial Separation:

  ○  ○  ○

  ○    ○   ○

  ○    |   ○

  □    |   □

  □    □   □

2. Identify Support Vectors and Optimal Hyperplane:

  ○  ○  ○
  ↑
  ○    ○   ○
            ↑
  ○----|----○
  ↑    |    ↑
  □----|----□
  ↑
  □    □   □

The vertical line represents the initial hyperplane.
The arrows point to the support vectors, the closest data points to the hyperplane.
The dashed line represents the optimal hyperplane, equidistant from the support vectors, maximizing the margin.

Non-linear SVM with Kernel Trick

In cases where the data isn't linearly separable in 2D, we use kernel functions to transform it into a higher-dimensional space.

1. Non-linearly Separable Data:

  ○  ○       □
       ○       □
     ○    ○
  □       ○      □
  □  □

2. Transform with Kernel Function and Separate in Higher Dimension:

Higher-Dimensional Space:
     □
   ○    ○
○    □
        ○   ○
□       □

The non-linearly separable data is transformed into a higher-dimensional space where it becomes linearly separable.
In this higher dimension, a linear hyperplane can separate the classes effectively.

SVMs for Linearly Separable Classes

In the two-class classification problem, we are given an input dataset containing two classes of data and an indicator function to map the data into classes. From the above figure, class 1 as C1 contains a set of positive samples whose indicator function value is +1, and class 2 as C2 contains a set of negative samples whose indicator function value is -1.
Then we try to find a linearly separable function, a hyperplane, which is defined as
f(W, X, w_o) = W.X+w_o ,
where W = set of weights defined on the input

X = input values

w_o= bias or a constant.

Let d+ and d- be the perpendicular distances from the separating hyperplane (margin lines), which are close to data points. The distance of the margin is defined as
d+ = W.X_i + w_o >= 1, for di = +1 for C1
d- = W.X_i + w_o <= -1, for di = -1 for C2

Let’s derive the margin:
We have SV1 (say X₊) and SV2 (say X_π) as support vectors. Then, we have
W.X₊ + w_o = 1 for C1 and similarly
W.X_π + w_o = 0 for C2.
Then from the above equations, we have W(X₊ - X_π) = 1
This above equation can be written as W( ||X₊ - X_π||. W / ||W||) = 1 => ||X₊ - X_π||. ||W||² / ||W|| = 1
At last, we get ||X₊ - X_π|| . ||W|| = 1 => ||X₊ - X_π|| = 1 / ||W||
Therefore, we can tell that the perpendicular distance will be concluded as d+ = d- = 1 / ||W||
Therefore total margin can be calculated as M = 2 / ||W||.
This can be diagrammatically shown below.

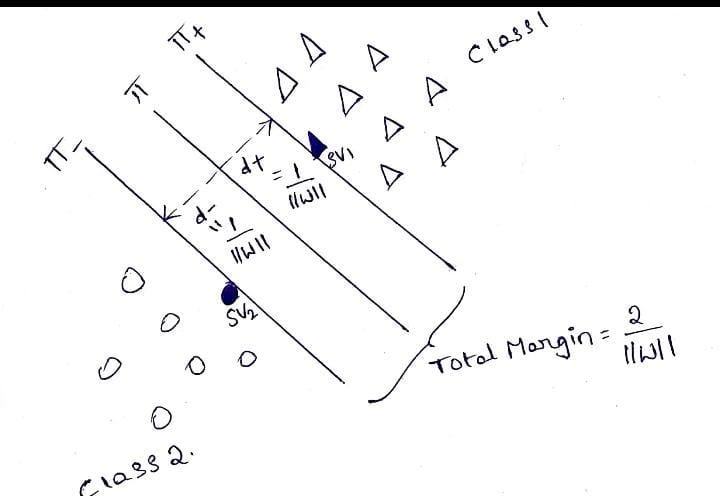
That's it. We find a hyperplane that separates two-class data points with a large margin.
Let’s have a look at the linearly inseparable case.

SVMs for Linearly Inseparable Classes

In the case of the non-separable dataset, the points of opposite classes may overlap. In this case, the constraints di(W.X + w_o) >= 1, for i = 1,2,.... cannot be satisfied for all data points.
We can also say that when the data points are scattered across the input space, identifying the margin line takes more time and more repetitions. Then, those data are called linearly non-separable data. To separate these data, we need to identify a soft margin that separates data in its most accurate way.
Here, we actually introduce a new slack variable to the class equations. Then we have
W.X_i + w_o >= 1 - 𝛏, di = +1
W.X_i + w_o <= -1 + 𝛏, di = -1 here the additional 𝛏 variable is called a slack variable, a constant. Here, we can say the introduction of the slack variable makes the soft margin classifier loss a hinge loss.

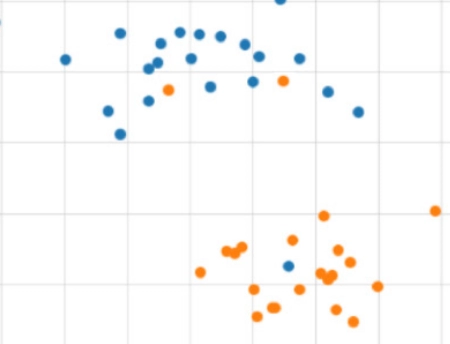
Linearly Inseparable Data

Then by doing the same process, we did for Linearly separable data to find the total margin, we can get a value of

M = 2( 1 - 2𝛏 ) / ||W||

There are more interesting features about SVMs, like using kernels in SVM. This will be a really broad topic to understand. Basically, these kernel functions are introduced to replace the dot function scenarios. Three admissible functions are

We will cover this concept later in our articles.

SVMs using scikit learn Python

Python’s scikit-learn library provides three ways of implementing the SVM classifier.
They are

svm.LinearSVC
svm.SVC ->gives an advantage of using kernels.
linear_model.SGDClassifier

You can go through these concepts in more detail through their official documentation linked above.

Advantages and Applications of SVM

SVMs can also be used for linearly Inseparable data using the kernel support.
It can also be used in the case of high dimensionality and even when the number of data points is smaller than its dimensionality.
It can also be used for Clustering(linearly Inseparable), Classification, and Regression problems.
Works well with even structured and unstructured data like text, images, etc.
The only disadvantage is it won't work well on large datasets when the dataset has more noise.

Disadvantages of Support Vector Machine (SVM)

SVMs take a long time to train on large datasets, making them less efficient for big data applications.
SVMs do not perform well when the dataset contains a lot of overlapping classes or noisy data.
Choosing the right kernel and hyperparameters requires trial and error, making optimization complex.
SVMs struggle with very large datasets due to high memory and processing requirements.
SVMs are mainly designed for binary classification and require extra techniques to handle multiple classes effectively.

Implement SVM Algorithm in Python

Code: Here, I will use a small example to demonstrate how SVMs are used to classify problems. We have used SciKit and a few other libraries for this. Let’s get to the code:

import numpy as np
X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
y = np.array([1, 1, 2, 2])

In the above three lines of code, we have defined two NumPy arrays. X has the points and Y has the classes to which these points belong to. Now, let us create our SVM model using sklearn.svm. Here, I choose the linear kernel.

from sklearn.svm import SVC
clf = SVC(kernel='linear')

We now fit out classifier(clf) to the data points we defined.
clf.fit(X, y)

To predict the class of a new dataset

prediction = clf.predict([[0,6]])

This would return us the prediction(a class to which the data belongs). Voila! It is simple to use an SVM for simple classification problems.

Real-World Applications of Support Vector Machines (SVM)

1. Face Detection: SVM separates parts of the image as facial and non-facial and forms a square border around the face.

2. Text and Hypertext Categorization: SVMs allow text and hypertext categorization for both inductive and transductive models. They use training data to classify documents into different categories. It categorizes based on the score generated and then compares it with the threshold value.

3. Classification of images: We have already discussed that SVMs are widely used in image classification problems. It provides better accuracy for image classification and image search in comparison to the formerly used query-based searching approaches.

4. Bioinformatics: SVMs are really popular in medical and bioinformatics and are used in protein classification and cancer classification problems. It is used for identifying the classification of genes, patients based on genes, and other biological problems like skin cancer.

5. Protein fold and remote homology detection: SVM algorithms are also widely used in protein remote homology detection.

6. Handwriting recognition: SVMs are used to recognize handwritten characters and work with a wide variety of languages.

7. Generalized Predictive Control (GPC): Use SVM based GPC to control chaotic dynamics with useful parameters and hyperparameters.

Frequently Asked Questions

What is the Support Vector Machine algorithm?

The Support Vector Machine (SVM) algorithm classifies data by finding the optimal hyperplane that separates different classes with the maximum margin.

What is the theory of SVM?

The theory of SVM involves maximizing the margin between support vectors of different classes to find the optimal hyperplane for classification.

What is the best algorithm for SVM?

The best algorithm for SVM often uses the Sequential Minimal Optimization (SMO) method, which efficiently solves the quadratic programming problem involved in training SVMs.

What does SVM stand for?

SVM stands for support vector machine. Basically, SVMs or support vector machines are used for both classification and regression tasks. It mainly saves the complexity. It improves the performance of tasks by implementing its kernel trick.

What is an SVM kernel?

An SVM kernel is a trick that is used by the support vector machine algorithm to improve its performance. These kernels are used to transform the input data space into the required form. For example, a kernel may take a low dimensional input space and transform it into a higher dimensional data space.

What is the agenda in the SVM concept?

The objective of the SVM is to perform classification and regression tasks by finding a linear indicator function, a hyperplane that separates two classes.

What are the advantages of using SVM?

SVMs are mainly used to reduce complexity. It can be used for both linearly separable and non-separable, for both classification and regression, and for structured and unstructured datasets.

Conclusion

In this article, we discussed the Support Vector Machine (SVM) algorithm, its working principle, and its applications in machine learning. We learned that SVM is a powerful classification and regression technique that uses hyperplanes to separate data points effectively. With the ability to handle high-dimensional data and various kernel functions, SVM remains a widely used algorithm in pattern recognition and predictive modeling. Understanding its advantages and limitations helps in selecting the right approach for different machine learning problems.