Symmetric Binary Tree

Introduction

A Symmetric binary tree is a type of binary tree in which the left part of the root node is identical to the mirror image of the right part and vice versa. We can understand symmetric binary trees with the help of the following diagram. 
 

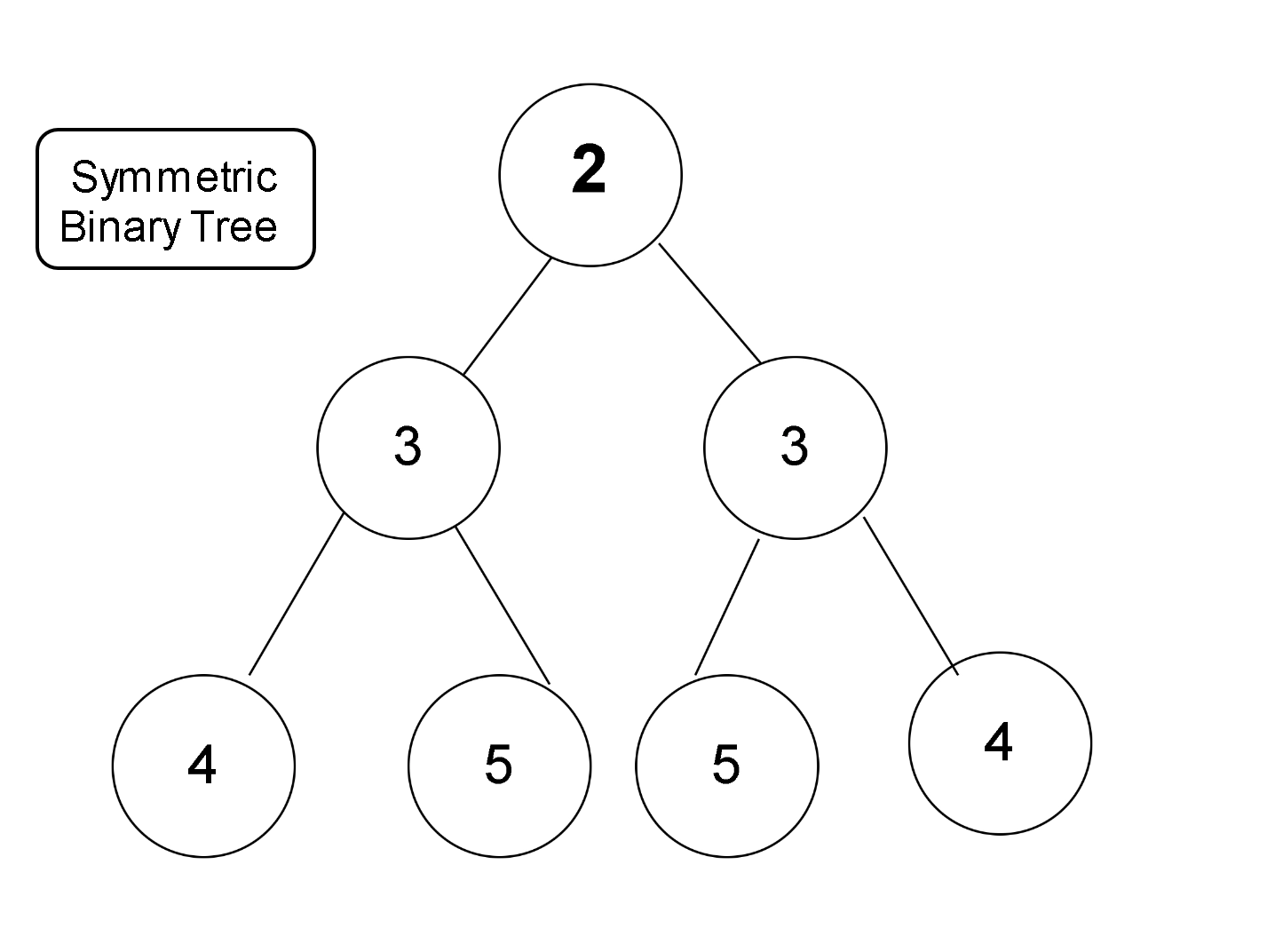
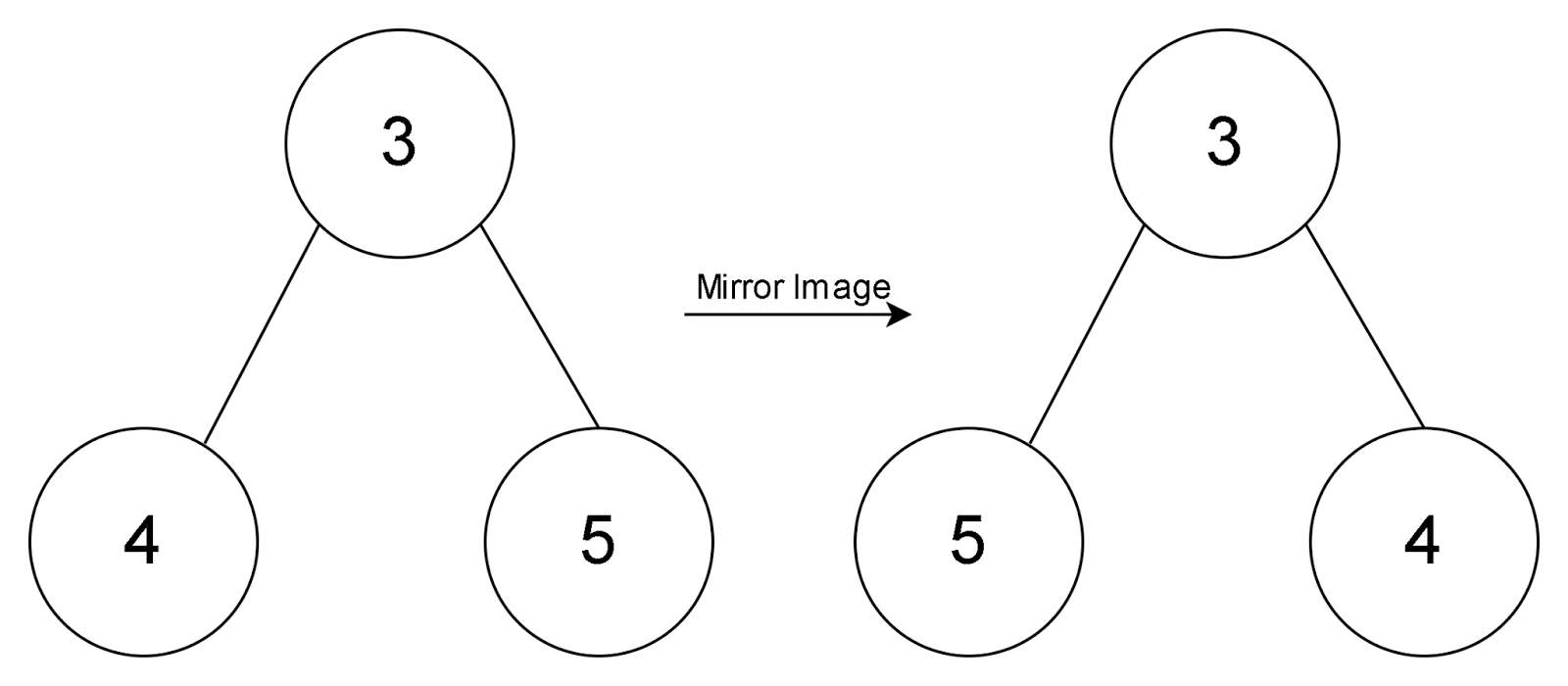
Here, the tree is a symmetric binary tree. We can understand the following with the help of the above definition. Let us divide the above binary tree into 2 parts and take the mirror image of one of the parts. We have taken the left subtree and made its mirror image. We find that the mirror image of the left subtree is similar to the right subtree. Hence the above tree is a symmetric binary tree. 
 

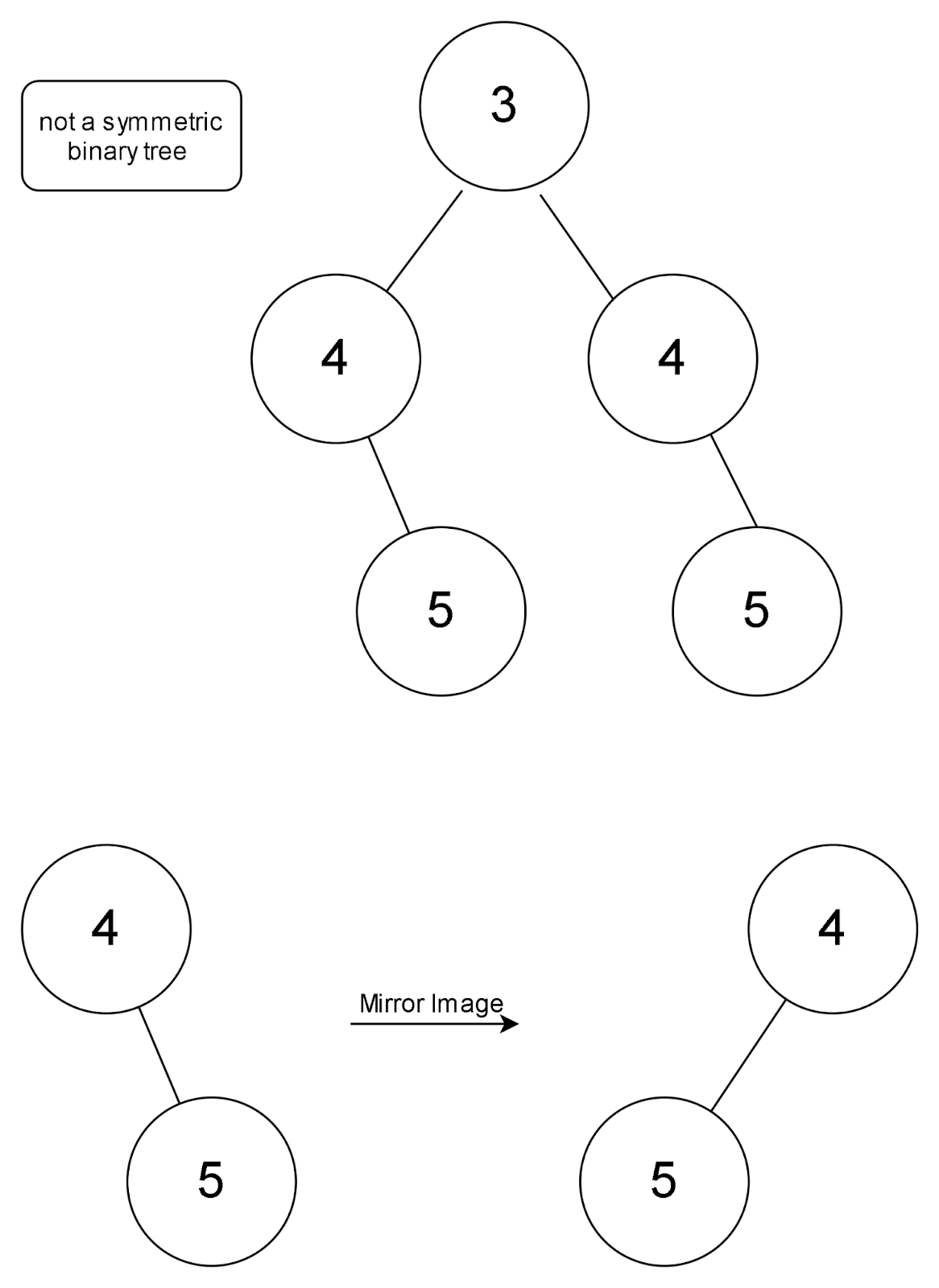
The below figure is not a symmetric binary tree as the mirror image of one of the subtrees is not equal to the other. Here in the below diagram, the mirror image of the left subtree is not equal to the right subtree as they differ in alignment.
 

The question we are going to discuss today in this blog is: Given a binary tree, check whether it is a symmetric binary tree or not.

Recommended: Try the Problem by yourself first before moving on to the solution.

Approach & Intuition 

We can analyze that the left and mirror images of the right half must be the same for the tree to be a symmetric binary tree. It is similar to checking the two trees simultaneously at every level. We can also observe that the trees will never be symmetric binary trees if one of the subtrees is null, and if they exist, their value must be the same. This leads us to the recursive approach, which goes like this - check for the left and right nodes of the root whether they both exist, and if they exist, then their value must be the same. We check recursively for every pair of nodes in the left and right subtree if this condition is true. 

Algorithm

We can solve this problem using a recursive algorithm which will be used to traverse the binary tree. This traversal is similar to depth-first search in the graph algorithm. Let us understand this algorithm with the help of the code below: 

Code in C++

#include<iostream>
 using namespace std; 
 
 struct Node {
     int val;
     Node *left;
     Node *right;
     Node(int x){
      val = x; Node* left = NULL; Node*right = NULL;
     }
  };
  
   
    bool solve(Node*a, Node*b){
       // if both left and right subtree are null then the tree is symmetric 
        if(a == NULL && b == NULL)return true; 
        // if both the tree are not null and there subtree are symmetric as well as the 
        // current values of the nodes are equal then we return true
        if(a && b && a->val == b->val && solve(a->left, b->right) && solve(a->right,  b->left))return true; 
        // in every other case(either one of a or b is null or the values of nodes a and b are unequal)  we will return false as the tree can't be symmetric
        return false; 
    }
    
    bool isSymmetric(Node* root) {
        // checking if root is null then the tree is always symmetric 
        if(root == NULL) return true; 
        // here we have seperated the left and the right subtree 
        return solve(root->left, root->right); 
        
    }
    
int main()
{
   // constructing the tree
    Node* root = new Node(2);
    root->left = new Node(3);
    root->right = new Node(3);
    root->left->left = new Node(4);
    root->left->right = new Node(5);
    root->right->left = new Node(5);
    root->right->right = new Node(4);
 
    if(isSymmetric(root))
      cout<<"Symmetric";
    else
      cout<<"Not symmetric";
    return 0;
}

You can also try this code with Online C++ Compiler

Run Code

Output :

Symmetric