Terms related to Probability

Probability Tree

The tree diagram helps organize and visualize the different possible outcomes. The probability of each branch is indicated on the branch, while the ends provide the eventual conclusion. Tree diagrams are used to determine when to multiply and when to add. The following is a tree diagram for throwing two coins:

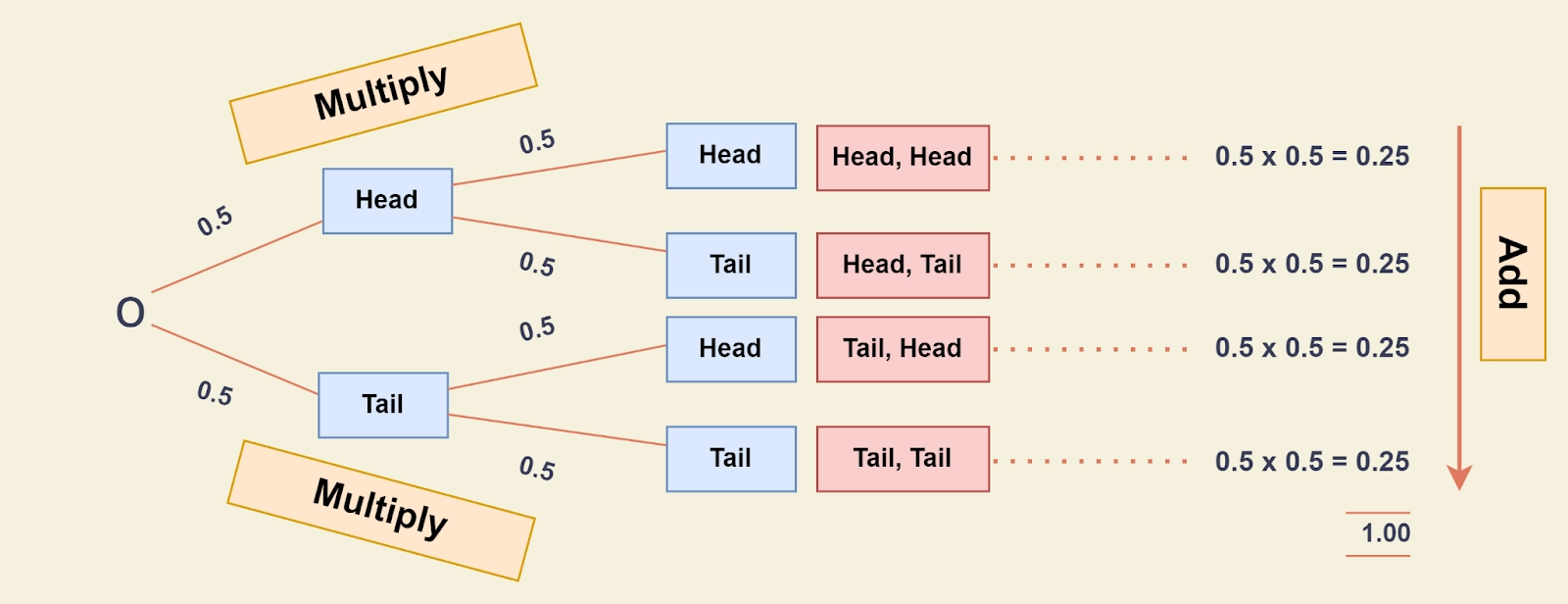
We can now see things like:

• "Head, Head" has a probability of 0.5 x 0.5 = 0.25.
• The sum of all probability equals 1.0. (which is always a good check)
• The odds of receiving at least one Head from two throws are 0.25+0.25+0.25 = 0.75.

Different types of probability

There are three types of probability:

• Theoretical Probability
• Experimental Probability
• Axiomatic Probability

Theoretical Probability

It is based on the probability of something happening. The reasoning behind probability is the foundation of theoretical probability. The theoretical probability of getting a tail while tossing a coin is 1/2.

Experimental Probability

It is based on the outcomes of an experiment. The experimental probability may be estimated by dividing the total number of trials by the number of potential outcomes. The Head is recorded 5 times, the experimental probability of heads is 5/8.

Axiomatic Probability

In axiomatic probability, a set of principles or axioms that apply to all sorts is developed. These axioms, known as Kolmogorov's three axioms, were established by Kolmogorov. The axiomatic approach to probability measures the chances of events happening or not happening. This topic is fully addressed in the axiomatic probability lesson, which covers Kolmogorov's three rules (axioms) and various examples.

The possibility of an event or outcome occurring dependent on a preceding event or outcome is known as conditional probability.
 

Probability of an Event

Let us assume that an event E can occur in x ways out of a sum of n possible equally likely ways. The event's likelihood of occurring or succeeding is then represented as;

P(E) = x/n

The probability that the event will not occur, often known as its failure, is represented as follows:

P(E') = (n-x)/n = 1 - (x/n) 

E' denotes that the event will not take place.

P(E) + P(E') = 1

This suggests that the sum of all probability in every random test or experiment equals 1.

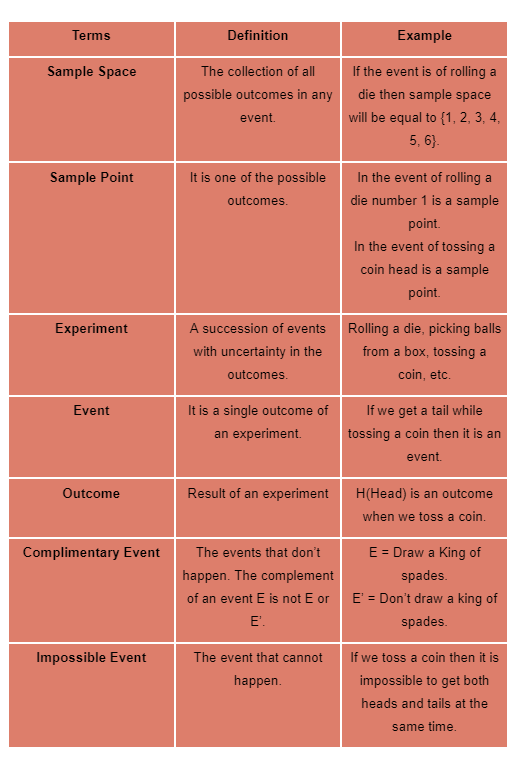
Terms related to probability

Applications of Probability

• Weather Planning: A probability prediction is a percentage-based evaluation of how probable an event is to occur, and it records the risks associated with weather.
   
• Sports Strategies: In sports, assessments are performed using probability to determine the strengths and weaknesses of a specific team or athlete. Analysts utilize probability and odds to forecast outcomes involving the performance of the team and its individuals in the sport.
   
• Insurance: These firms employ the theory of probability or theoretical probability when developing a policy or determining a premium rate. The theory of probability is a statistical strategy for predicting the potential of future outcomes.
   
• Games: Probability is used in blackjack, poker, gambling, all sports, board games, and video games to determine how probable a team or individual is to win.

Sample Questions

Q1) Find the probability of getting a 1 on a rolling die.

Solution:

Sample Space (S) = {1, 2, 3, 4, 5, 6}
Total number of Outcomes = n(S) = 6
Let E denote the event of getting 1. 
Favorable outcomes n(E)= 1.
Probability P(E) = n(E) / n(S) = 1/6 
Probability of getting a 1 on a rolling die = 1/6 

Q2) Three coins are tossed simultaneously then find the probability of

1. Getting at least 2 heads
2. Getting at max 1 head
3. Getting 3 tails       
    

Solution:                

Sample Space (S) = {HHH, HHT, HTT, HTH, TTT, TTH, THH, THT}
Therefore total no of outcomes n(S) = 8.
 
1. E = event for getting at least 2 heads in an outcome
   n(E) = {HHH, HHT, HTH, THH} = 4
   Probability of getting at least 2 heads = 4/8 = 1/2 
 
2. E = event for getting at max 1 head in an outcome
   n(E) = {HTT, TTT, TTH, THT} = 4
   Probability of getting at max 1 head = 4/8 = 1/2

3. E = event for getting three tails in an outcome
   n(E) = {TTT} = 1
   Probability of getting three tails = 1/8 

Q3) If we draw a random card from a deck of cards, then what is the probability that the drawn card is a face card from hearts is?

Solution:

As we all know that a deck has 52 cards.
The total number of outcomes n(S) = 52
E = event of drawing a card from hearts
n(E) = 4 (because hearts has a total of 13 cards in it and there are 4 face cards)
P = n(E) / n(S) = 4/52 = 1/13
The probability of getting a face card from hearts is 1/13.

FAQs

1. Can probability have negative values?
   No probability cannot have a negative value.
    
2. What is an equally likely outcome?
   Equally likely outcomes are the results of an experiment in which each of the outcomes has an equal probability. The likelihood of receiving any number while rolling a six-sided die is equal.
    
3. What is a random variable?
   A random variable is a variable whose value results from random phenomena, such as the outcome of rolling a dice, where the procedure is fixed, but the outcome is not.

Key Takeaways

In this blog, we have briefly discussed probability and different terms related to probability, and we have also discussed some questions of probability. 

We hope that this blog has helped you enhance your knowledge regarding this topic of probability and if you want to learn more about such interesting topics, you can look at our platform Coding Ninjas Studio. Do upvote our blog and help other ninjas grow. Happy Coding!