Approach
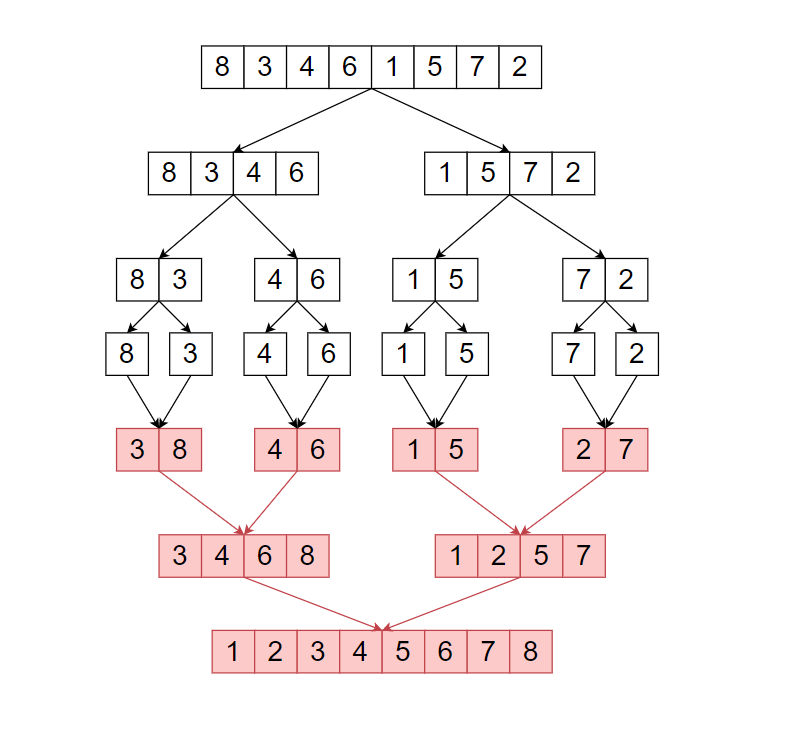
In the image above, we can see the functioning of the merge sort. In merge sort, we divide the list into two smaller lists at each step and call the same function recursively on both the smaller parts. From recursion, we get two sorted lists which are then merged by a function, let’s say, merge(), and the final output is a sorted list.
But how will we apply this to doubly linked lists?
The answer is simple. We will first find the middle node of the linked list. You can refer here to find the middle node of a linked list. Then we will split the linked list around the middle node and make two recursive calls on both these sub-linked lists. Finally, we will be merging the two sorted lists (returned from the recursive calls above).
How to code the merge() function?
The function will take two parameters,i.e., ‘FIRST_LIST’ and ‘SECOND_LIST’, and will check for the following cases:
1) If ‘FIRST_LIST’ is NULL, return ‘SECOND_LIST’.
2) If ‘SECOND_LIST’ is null, return ‘FIRST_LIST’.
3) If ‘FIRST_LIST->DATA’ is less than ‘SECOND_LIST->DATA’, then we will append ‘FIRST_LIST’ to the resultant list otherwise we will append ‘SECOND_LIST’.
Now let’s have a look at the final code for better understanding.
Code
#include <iostream>
using namespace std;
// Doubly linked list node class.
class Node
{
public:
int data;
Node *next, *prev;
// Constructor.
Node(int data)
{
this->data = data;
next = NULL;
prev = NULL;
}
};
// This function divides the linked list into two parts and returns the head of second half.
Node *split(Node *head)
{
Node *slowPointer = head;
Node *fastPointer = head;
while (fastPointer != NULL && fastPointer->next != NULL &&
fastPointer->next->next != NULL)
{
fastPointer = fastPointer->next->next;
slowPointer = slowPointer->next;
}
Node *secondHalf = slowPointer->next;
// Separating the second part.
slowPointer->next = NULL;
return secondHalf;
}
// This function will merge two lists and will return the sorted list.
Node *merge(Node *firstList, Node *secondList)
{
// If the 'firstList' linked list is empty, then we dont have to merge.
if (firstList == NULL)
return secondList;
// If the 'secondList' linked list is empty, then don’t have to merge.
if (secondList == NULL)
return firstList;
// Regular merge conditions.
if (firstList->data > secondList->data)
{
secondList->next = merge(firstList, secondList->next);
secondList->next->prev = secondList;
secondList->prev = NULL;
return secondList;
}
else
{
firstList->next = merge(firstList->next, secondList);
firstList->next->prev = firstList;
firstList->prev = NULL;
return firstList;
}
}
// It returns the sorted doubly linked list.
Node *mergeSort(Node *head)
{
if (head == NULL) {
return head;
}
if (head->next == NULL) {
return head;
}
Node *firstList = NULL, *secondList = NULL;
// Splitting the list.
secondList = split(head);
// Recursively calling merge sort on both the sublists.
firstList = mergeSort(head);
secondList = mergeSort(secondList);
// Merging the two sorted sub lists.
Node *sortedList = merge(firstList, secondList);
return sortedList;
}
// Print function.
void print(Node *head)
{
Node *temp = head;
while (temp != NULL)
{
cout << temp->data << " ";
temp = temp->next;
}
}
// Main function.
int main()
{
int n;
cout << "Enter the number of elements in the list: ";
cin >> n;
cout << "Enter the elements: ";
Node *head = NULL, *tail = NULL;
for (int i = 0; i < n; i++)
{
int data;
cin >> data;
Node *newNode = new Node(data);
if (i == 0)
{
head = tail = newNode;
}
else
{
tail->next = newNode;
newNode->prev = tail;
tail = newNode;
}
}
cout << "Sorted list: ";
// Calling the 'mergeSort()' function to sort the doubly linked list.
head = mergeSort(head);
// Printing the final list.
print(head);
return 0;
}

You can also try this code with Online C++ Compiler
Input
Enter the number of elements in the list: 6
Enter the elements: 8 9 12 2 18 20
Output
Sorted list: 2 8 9 12 18 20
Complexities
Time Complexity
O(N * log N), where ‘N’ is the length of the array.
Here in the worst case split operation takes O(N), the merge operation takes O(N) time and the recursive function will be called O(log N) times so the overall complexity would be (O(N) + O(N)) * O(log(N)) ~ O(N * log(N)).
Space Complexity
O(log (N)), where ‘N’ is the length of the doubly linked list.
As we are using a recursive function and it would take O(log (N)) space for the recursive stack.
Frequently Asked Questions
What is a linked list?
A linked list is a dynamic data structure in which each element (called a node) consists of two components: data and a reference (or pointer) to the next node. A linked list is a collection of nodes, each of which is linked to the next node by a pointer.
How is the linked list implemented in memory?
LinkedList, unlike Arrays, is not stored in a contiguous memory location. Each element in the list is distributed across memory and is linked by pointers in the Node. As a result, separate memory space is allocated large enough to store both the key and the pointer to the next element whenever a new element is added.
What is the use of a doubly linked list?
It is used in navigation systems where both forward and backward navigation is required. The browser uses a back and forward button to implement backward and forward navigation of visited web pages. It is also used to represent a traditional card game deck.
Conclusion
We saw how we could apply merge sort on doubly linked lists and also revised concepts on finding the middle part of and merging doubly-linked lists. Now doubly linked lists is a vast topic, and this was just the beginning of your journey in becoming a star coder.
Recommended Problems -
Recommended Reading:
Do check out The Interview guide for Product Based Companies as well as some of the Popular Interview Problems from Top companies like Amazon, Adobe, Google, Uber, Microsoft, etc. on Coding Ninjas Studio.
Also check out some of the Guided Paths on topics such as Data Structure and Algorithms, Competitive Programming, Operating Systems, Computer Networks, DBMS, System Design, etc. as well as some Contests, Test Series, Interview Bundles, and some Interview Experiences curated by top Industry Experts only on Coding Ninjas Studio.
Cheers!








